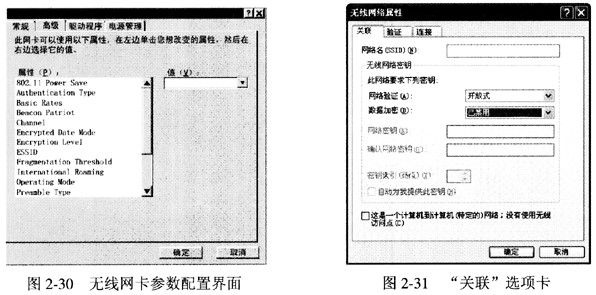
该图书馆无线阅览室的WLAN网搭建完成后,读者小郭需要在该阅览室公告栏上查看无线网卡的相关配置参数,进行正确设置后方可访问因特网。请结合图2-30所示的无线网卡参数的配置界面,指出小郭应从公告栏中重点查看哪4个配置参数?
题目
该图书馆无线阅览室的WLAN网搭建完成后,读者小郭需要在该阅览室公告栏上查看无线网卡的相关配置参数,进行正确设置后方可访问因特网。请结合图2-30所示的无线网卡参数的配置界面,指出小郭应从公告栏中重点查看哪4个配置参数?
相似考题
更多“ 该图书馆无线阅览室的WLAN网搭建完成后,读者小郭需要在该阅览室公告栏上查看无线网卡的相关配置参数,进行正确设置后方可访问因特网。请结合图2-30所示的无线网卡参数的配置界面,指出小郭应从公告栏中重点查看哪4个配”相关问题
-
第1题:
阅读以下算法说明和问题模型图,根据要求回答问题1、问题2。
[说明]
某大学城图书馆需要在无线阅览厅的某些位置上放置无线接入点AP(Access Poin)。假设每个无线 AP覆盖范围的半径是6米,因此必须使得每台笔记本电脑上的无线网卡到某个无线AP的直线距离不超过6米。为了简化问题,假设所有无线网卡在同一直线上,并且无线AP沿该直线放置。该问题可以建模为如图1-13所示,其中直线表示无线网卡所在的直线,实心正方形表示无线网卡。现采用贪心策略实现用尽可能少的无线AP覆盖所有的无线网卡。

实现贪心算法的流程如图1-14所示。其中,①d[i](1≤i≤N)表示第i张无线网卡到通道A端的距离,N表示无线网卡的总数,无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号:②s[k]表示第k(k≥1)个无线AP到通道A端的距离。算法结束后k的值为无线AP的总数。

请填补图1-14流程图中(1)~(4)空缺处的内容。
正确答案:本试题的题干说明中已将无线网卡分布问题建模(如图1-13所示)。其中直线表示无线网卡所在的直线实心正方形表示无线网卡。而要求解的问题是要求如何在该直线上布局无线AP使其能覆盖所有的无线网卡并且所用无线AP的数量要尽可能的少。这是一个通过进行一系列选择求最优解的问题。 分析该问题发现其具有最优子结构并且具有贪心选择性质故该问题可以用贪心算法来求解。贪心算法思想是:问题的规模为N从第1个无线网卡(最左端)开始布局无线AP把第1个无线AP放置在该无线网卡右方的6米处此时该无线AP会覆盖从第1个无线网卡到该无线网卡右方直线长度为12米的所有无线网卡假设覆盖了N1个无线网卡。此时问题规模变成了N-N1接着把第1个无线AP覆盖的无线网卡去掉再从N-N1中选择第1个(最左端)无线网卡开始布局无线AP将第2个无线AP放置在该无线网卡右方的6米处。依此布局直到覆盖所有的无线网卡。 图1-22是问题解的模型。其中直线表示无线网卡所在的直线实心正方形表示无线网卡实心圆形表示无线AP虚线圆以对应无线AP为圆心直径为无线AP的覆盖范围即对应无线AP的覆盖范围(12米)。 实现贪心算法的流程见题干的图1-14。由于“算法结束后k的值为无线AP的总数”因此在算法开始处需要对变量k赋初值即(1)空缺处所填写的内容是“k=0”。
该贪心算法中N表示无线网卡的总数且无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号d[i](1≤i≤N)表示第i个无线网卡到通道A端的距离。当判断第i个无线网卡未超过无线网卡总数N而求解下一个无线网卡(即第i+1个无线网卡或第j个无线网卡)所归属的无线AP时也需要判断第j个无线网卡是否超过无线网卡总数N以及第j个无线网卡与第i个无线网卡之间的距离是否超过12米因此(2)空缺处所在的判断条件是“j=N&&d[j]-d[i]=12”即该空缺处所填写的内容是“j=N”或其等价形式。
若第j个无线网卡未超过无线网卡总数N且第j个无线网卡与第i个无线网卡之间的距离未超过12米则可以求解再下一个无线网卡(即第i+2个无线网卡或第j+1个无线网卡)所归属的无线AP。反之则需要记录无线AP的总数k即(3)空缺处所填写的内容是“k=k+1”或其等价形式;以及记录第k(k1)个无线AP到通道A端的距离即(4)空缺处所填写的内容是“d[i]+6”或其等价形式。
当求解完第k个无线AP(覆盖了N1个无线网卡)的布局后需要把第k个无线AP覆盖的无线网卡去掉再从N-N1中选择第1个(最左端)无线网卡开始布局第k+1个无线AP。依此不断求解直到覆盖所有的无线网卡。
实现贪心算法的流程见题干的图1-14。由于“算法结束后k的值为无线AP的总数”因此在算法开始处需要对变量k赋初值即(1)空缺处所填写的内容是“k=0”。
该贪心算法中N表示无线网卡的总数且无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号d[i](1≤i≤N)表示第i个无线网卡到通道A端的距离。当判断第i个无线网卡未超过无线网卡总数N而求解下一个无线网卡(即第i+1个无线网卡或第j个无线网卡)所归属的无线AP时也需要判断第j个无线网卡是否超过无线网卡总数N以及第j个无线网卡与第i个无线网卡之间的距离是否超过12米因此(2)空缺处所在的判断条件是“j=N&&d[j]-d[i]=12”即该空缺处所填写的内容是“j=N”或其等价形式。
若第j个无线网卡未超过无线网卡总数N且第j个无线网卡与第i个无线网卡之间的距离未超过12米则可以求解再下一个无线网卡(即第i+2个无线网卡或第j+1个无线网卡)所归属的无线AP。反之则需要记录无线AP的总数k即(3)空缺处所填写的内容是“k=k+1”或其等价形式;以及记录第k(k1)个无线AP到通道A端的距离即(4)空缺处所填写的内容是“d[i]+6”或其等价形式。
当求解完第k个无线AP(覆盖了N1个无线网卡)的布局后需要把第k个无线AP覆盖的无线网卡去掉再从N-N1中选择第1个(最左端)无线网卡开始布局第k+1个无线AP。依此不断求解直到覆盖所有的无线网卡。
本试题的题干说明中已将无线网卡分布问题建模(如图1-13所示)。其中,直线表示无线网卡所在的直线,实心正方形表示无线网卡。而要求解的问题是要求如何在该直线上布局无线AP,使其能覆盖所有的无线网卡,并且所用无线AP的数量要尽可能的少。这是一个通过进行一系列选择求最优解的问题。 分析该问题,发现其具有最优子结构,并且具有贪心选择性质,故该问题可以用贪心算法来求解。贪心算法思想是:问题的规模为N,从第1个无线网卡(最左端)开始布局无线AP,把第1个无线AP放置在该无线网卡右方的6米处,此时该无线AP会覆盖从第1个无线网卡到该无线网卡右方直线长度为12米的所有无线网卡,假设覆盖了N1个无线网卡。此时问题规模变成了N-N1,接着把第1个无线AP覆盖的无线网卡去掉,再从N-N1中选择第1个(最左端)无线网卡开始布局无线AP,将第2个无线AP放置在该无线网卡右方的6米处。依此布局,直到覆盖所有的无线网卡。 图1-22是问题解的模型。其中,直线表示无线网卡所在的直线,实心正方形表示无线网卡,实心圆形表示无线AP,虚线圆以对应无线AP为圆心,直径为无线AP的覆盖范围,即对应无线AP的覆盖范围(12米)。 实现贪心算法的流程见题干的图1-14。由于“算法结束后k的值为无线AP的总数”,因此在算法开始处需要对变量k赋初值,即(1)空缺处所填写的内容是“k=0”。
该贪心算法中,N表示无线网卡的总数,且无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号,d[i](1≤i≤N)表示第i个无线网卡到通道A端的距离。当判断第i个无线网卡未超过无线网卡总数N,而求解下一个无线网卡(即第i+1个无线网卡,或第j个无线网卡)所归属的无线AP时,也需要判断第j个无线网卡是否超过无线网卡总数N,以及第j个无线网卡与第i个无线网卡之间的距离是否超过12米,因此(2)空缺处所在的判断条件是“j=N&&d[j]-d[i]=12”,即该空缺处所填写的内容是“j=N”或其等价形式。
若第j个无线网卡未超过无线网卡总数N,且第j个无线网卡与第i个无线网卡之间的距离未超过12米,则可以求解再下一个无线网卡(即第i+2个无线网卡,或第j+1个无线网卡)所归属的无线AP。反之,则需要记录无线AP的总数k,即(3)空缺处所填写的内容是“k=k+1”或其等价形式;以及记录第k(k1)个无线AP到通道A端的距离,即(4)空缺处所填写的内容是“d[i]+6”或其等价形式。
当求解完第k个无线AP(覆盖了N1个无线网卡)的布局后,需要把第k个无线AP覆盖的无线网卡去掉,再从N-N1中选择第1个(最左端)无线网卡开始布局第k+1个无线AP。依此不断求解,直到覆盖所有的无线网卡。
实现贪心算法的流程见题干的图1-14。由于“算法结束后k的值为无线AP的总数”,因此在算法开始处需要对变量k赋初值,即(1)空缺处所填写的内容是“k=0”。
该贪心算法中,N表示无线网卡的总数,且无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号,d[i](1≤i≤N)表示第i个无线网卡到通道A端的距离。当判断第i个无线网卡未超过无线网卡总数N,而求解下一个无线网卡(即第i+1个无线网卡,或第j个无线网卡)所归属的无线AP时,也需要判断第j个无线网卡是否超过无线网卡总数N,以及第j个无线网卡与第i个无线网卡之间的距离是否超过12米,因此(2)空缺处所在的判断条件是“j=N&&d[j]-d[i]=12”,即该空缺处所填写的内容是“j=N”或其等价形式。
若第j个无线网卡未超过无线网卡总数N,且第j个无线网卡与第i个无线网卡之间的距离未超过12米,则可以求解再下一个无线网卡(即第i+2个无线网卡,或第j+1个无线网卡)所归属的无线AP。反之,则需要记录无线AP的总数k,即(3)空缺处所填写的内容是“k=k+1”或其等价形式;以及记录第k(k1)个无线AP到通道A端的距离,即(4)空缺处所填写的内容是“d[i]+6”或其等价形式。
当求解完第k个无线AP(覆盖了N1个无线网卡)的布局后,需要把第k个无线AP覆盖的无线网卡去掉,再从N-N1中选择第1个(最左端)无线网卡开始布局第k+1个无线AP。依此不断求解,直到覆盖所有的无线网卡。
-
第2题:
建立一个家庭无线局域网,使计算机不但能够连接到因特网,而且在WLAN内部还可以直接通信。正确的组网方案是
A.AP+无线网卡 B.无线天线+无线ModemC.无线路由器+无线网卡 D.AP+无线路由器
正确答案:C
单纯性无线AP就是一个无线的交换机,它仅提供无线信号发射功能。单纯性无线AP的工作原理是将网络信号通过双绞线传送过来,经过AP的编译,将电信号转换成无线电信号发送出去,形成无线网的覆盖。根据不同的功率,可以实现不同程度、不同范围的网络覆盖。无线AP的最大覆盖距离通常可达300米。多数单纯性无线AP本身不具备路由功能,包括DNS、DHCP、Firewall在内的服务器功能都必须由独立的路由器或计算机来完成。
在本题中,为了在组建家庭局域网的同时完成Internet接入,无线路由器是必选设备,剩下的工作只是需要安装无线网卡了。 -
第3题:
● 建立一个家庭无线局域网,使得计算机不但能够连接因特网,而且WLAN内部还可以直接通信,正确的组网方案是 (66) 。
(66)
A. AP+无线网卡
B. 无线天线+无线MODEM
C. 无线路由器+无线网卡
D. AP+无线路由器
正确答案:C
-
第4题:
阅读以下技术说明和问题模型图,根据要求回答问题1和问题2。
【说明】
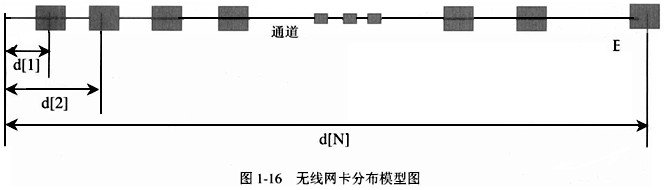
某大学城图书馆需要在无线阅览厅的某些位置上放置无线接入点AP(Access Poin)。假设每个无线AP覆盖范围的半径是6米,因此必须使得每台笔记本电脑上的无线网卡到某个无线AP的直线距离不超过6米。为了简化问题,假设所有无线网卡在同一直线上,并且无线AP沿该直线放置。该问题可以建模为如图1-16所示,其中直线表示无线网卡所在的直线,实心正方形表示无线网卡。现利用贪心策略实现用尽可能少的无线AP覆盖所有的无线网卡。
实现贪心算法的流程如图1-17所示。其中,①d[i](1≤i≤N)表示第i张无线网卡到通道A端的距离,N表示无线网卡的总数,无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号;②s[k]表示第k(k≥1)个无线AP到通道A端的距离。算法结束后k的值为无线AP的总数。
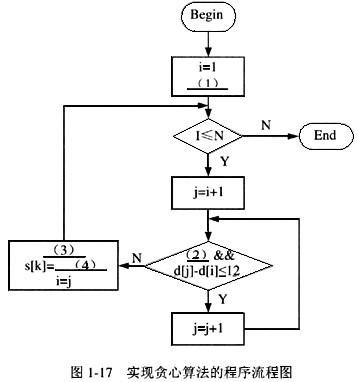
请填补图1-17流程图中(1)-(4)空缺处的内容。
正确答案:(1)k=0 (2)j=N或其等价形式 (3)k=k+1或其等价形式 (4)d[i]+6或其等价形式
(1)k=0 (2)j=N或其等价形式 (3)k=k+1或其等价形式 (4)d[i]+6或其等价形式 解析:本试题的题干说明中已将无线网卡分布问题建模(如图1-16所示)。其中,直线表示无线网卡所在的直线,实心正方形表示无线网卡。而要求解的问题是要求如何在该直线上布局无线AP,使其能覆盖所有的无线网卡,并且所用无线AP的数量要尽可能的少。这是一个通过进行一系列选择求最优解的问题。
分析该问题,发现其具有最优子结构,并且具有贪心选择性质,故该问题可以用贪心算法来求解。贪心算法思想是:问题的规模为N,从第1个无线网卡(最左端)开始布局无线AP,把第1个无线AP放置在该无线网卡右方的6m处,此时该无线AP会覆盖从第1个无线网卡到该无线网卡右方直线长度为12m的所有无线网卡,假设覆盖了N1个无线网卡。此时问题规模变成了N-N1,接着把第1个无线AP覆盖的无线网卡去掉,再从N-N1中选择第1个(最左端)无线网卡开始布局无线AP,将第2个无线AP放置在该无线网卡右方的6m处。依此布局,直到覆盖所布的无线网卡。
图1-20是问题解的模型。其中,直线表示无线网卡所在的直线,实心正方形表示无线网卡,实心圆形表示无线AP,虚线圆以对应无线AP为圆心,直径为无线AP的覆盖范围,即对应无线AP的覆盖范围(12米)。

实现贪心算法的流程见图1-17。由于“算法结束后k的值为无线AP的总数”,因此在算法开始处需要对变量k赋初值,即(1)空缺处所填写的内容是“k=0”。
该贪心算法中,N表示无线网卡的总数,且无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号,d[i]1≤i≤N)表示第i个无线网卡到通道A端的距离。当判断第i个无线网卡未超过无线网卡总数N,而求解下一个无线网卡(即第i+1个无线网卡,或第j个无线网卡)所归属的无线AP时,也需要判断第j个无线网卡是否超过无线网卡总数N,以及第j个无线网卡与第j个无线网卡之间的距离是否超过12米,因此(2)空缺处所在的判断条件是“j=N&&d[i]-d[i]=12”,即该空缺处所填写的内容是“j=N”或其等价形式。
若第j个无线网卡未超过无线网卡总数N,且第j个无线网卡与第j个无线网卡之间的距离未超过12米,则可以求解再下一个无线网卡(即第i+2个无线网卡,或第j+1个无线网卡)所归属的无线AP。反之,则需要记录无线AP的总数k,即(3)空缺处所填写的内容是“k=k+1”或其等价形式;以及记录第A(A)1)个无线AP到通道A端的距离,即(4)空缺处所填写的内容是“d[i]+6”或其等价形式。
当求解完第k个无线AP(覆盖了N1个无线网卡)的布局后,需要把第A个无线AP覆盖的无线网卡去掉,再从N-N1中选择第1个(最左端)无线网卡开始布局第k+1个无线AP。依此不断求解,直到覆盖所有的无线网卡。 -
第5题:
是用于在无线局域网中使用的网卡,主要采用的是蓝牙技术、802.11
A.802.11b技术。
B.WLAN网卡
C.单模无线网卡
D.双模无线网卡
E.CDMA无线网卡
正确答案:A
