itgle.com

已知一棵度为k的树中有n1个度为1的结点，n2个度为2的结点，…，nk个度为k的结点，则该树中叶子结点数为(30)。A．B．C．D．

题目

已知一棵度为k的树中有n1个度为1的结点，n2个度为2的结点，…，nk个度为k的结点，则该树中叶子结点数为(30)。

A．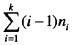

B．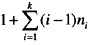

C．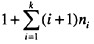

D．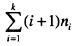

相似考题

1.已知一棵度为3的树有2个度为1的结点,3个度过为2的结点,4个度为3的结点,则该树中有12个叶子结点。()此题为判断题(对，错)。

2.某二叉树中有n个度为2的结点，则该二叉树中的叶子结点数为A．n+lB．n-1C．2nD．n/2

3.某二叉树中有15个度为1的结点，16个度为2的结点，则该二叉树中总的结点数为()。A.32B.46C.48D.49

4.如果在一棵二叉树中有17个度为2的结点，则该二叉树中有_______个叶子结点。

更多“已知一棵度为k的树中有n1个度为1的结点，n2个度为2的结点，…，nk个度为k的结点，则该树中叶子结点数为(30)。A．B．C．D．”相关问题

  • 第1题：

    一棵二叉树有10个度为l的结点，7个度为2的结点，则该二叉树共有_______个结点。


    正确答案：25
    25 解析：在任意一棵二叉树中，度数为0的结点(即叶子结点)总比度为2的结点多一个，因此该二叉树中叶子结点为7+1=8，8+17=25。

  • 第2题：

    一棵二叉树中共有70个叶子结点与80个度为1的结点，则该二又树中的总结点数为

    A．219

    B．221

    C．229

    D．231


    正确答案：A
    解析：在任意一棵二叉树中，若终端结点(叶子结点)的个数为n1，则度为2的结点数n2=n1-1。本题中度为0的结点即叶子结点，故总结点数二度为0的结点数+度为1的结点数+度为2的结点数=70+80+69=219。

  • 第3题：

    一棵二叉树有10个度为1的结点，7个度为2的结点，则该二义树共有【 】个结点。


    正确答案：25
    25

  • 第4题：

    某二又树有5个度为2的结点,则该二叉树巾的叶子结点数是( )。 A.10B.8C.6SX

    某二又树有5个度为2的结点，则该二叉树巾的叶子结点数是（ ）。

    A.10

    B.8

    C.6

    D.4


    正确答案：C
    C。【解析】根据二叉树的性质，在任意二叉树中，度为0的结点(即叶子结点)总是比度为2的结点多一个。

  • 第5题：

    若一棵度为7的树有8个度为1的结点，有7个度为2的结点，有6个度为3的结点，有5个度为4的结点，有4个度为5的结点，有3个度为6的结点，有2个度为7的结点，则该树一共有(48)叶结点。

    A．35

    B．36

    C．77

    D．78


    正确答案：D
    解析：n-1=所有结点度之和，所以有：n-1=8×1+7×2+6×3+5×4+4×5+3×6+2×7，即n=113；又因为n=n0+n1+n2+n3+n4+n5+n6+n7所以有113=n0+8+7+6+5+4+3+2，所以叶结点数n0为78。

  • 第6题：

    一棵二叉树有10个度为1的结点，7个度为2的结点，则该二叉树共有【 】个结点。


    正确答案：25
    25

  • 第7题：

    ● 已知一棵度为 3 的树（一个结点的度是指其子树的数目，树的度是指该树中所有结点的度的最大值）中有 5 个度为 1 的结点，4 个度为 2 的结点，2 个度为 3 的结点，那么，该树中的叶子结点数目为 （61） 。

    （61）

    A. 10

    B. 9

    C. 8

    D. 7


    正确答案：B

  • 第8题：

    己知一棵度为3的树（一个结点的度是指其子树的数目，树的度是指该树中所有结点的度的最大值）中有5个度为1的结点，4个度为2的结点，2个度为3的结点，那么，该树中的叶子结点数目为（ ）。

    A.10
    B.9
    C.8
    D.7

    答案：B
    解析：
    由于叶子节点没有子树，因此它的度为0。而除根节点外，其它的节点都应该可以做为子节点，即可以用于计算度。在本题中告我有5个度为1的结点，4个度为2的结点，2个度为3的结点，那么树中总的度数为5+8+6=19，因此树中除根节点外，就应该有19个节点，所以树中总的节点数应该为20，那么叶子节点数=20-5-4-2=9。

  • 第9题：

    一棵二叉树中共有69个度为2的结点与80个度为1的结点，则该二又树中的总结点数为

    A.22l
    B.219
    C.231
    D.229

    答案：B
    解析：
    二叉树有一个性质：在任意一棵二叉树中，度为0的结点(即叶子结点)总是比度为2的结点多一个。由于本题中的二叉树有70个叶子结点，因此有69个度为2的结点该二叉树中总的结点数为度为2的结点数+度为1的结点数+叶子结点数=69+80+70=219

  • 第10题：

    已知一棵度为3的树有2个度为1的结点，3个度为2的结点，4个度为3的结点。则该树中有（）个叶子结点。


    正确答案:12

  • 第11题：

    填空题
    已知一棵度为3的树有2个度为1的结点，3个度为2的结点，4个度为3的结点。则该树中有（）个叶子结点。

    正确答案： 12
    解析： 根据二叉树性质 3 的证明过程，有 n0=n2+2n3+1（n0、n2、n3 分别为叶子结点、度为 2 的结点 和度为 3 的结点的个数）。

  • 第12题：

    单选题
    设一棵二又树中有3个叶子结点，有8个度为1的结点，则该二又树中总的结点数为(  )
    A

    12

    B

    13

    C

    14

    D

    15


    正确答案： A
    解析：

  • 第13题：

    若一棵三次树中有两个度为3的结点,一个度为2的结点,两个度为1的结点,该树一共有()结点。

    A.5

    B.8

    C.10

    D.11


    参考答案：D

  • 第14题：

    设一棵二叉树中有3个叶子结点，有8个度为1的结点，则该二叉树牛总的结点数为【 】。


    正确答案：13
    13 解析：根据二叉树的性质3：在任意一棵二叉树中，度为0的结点(即叶子结点)总是比度为2的结点多一个。本题中的二叉树有3个叶子结点，所以，该二叉树有3-1=2个度为2的结点；又知本题中的二叉树有8个度为1的结点。所以，本题中的二叉树总结点数为叶子结点数+度为1的结点数+度为2的结点数 =3+8+2=13.所以，本题的正确答案为13。

  • 第15题：

    某二叉树有5个度为2的结点,则该二叉树中的叶子结点数是( )。 A.10B.8C.6SX

    某二叉树有5个度为2的结点，则该二叉树中的叶子结点数是（ ）。

    A.10

    B.8

    C.6

    D.4


    正确答案：C
    C。【解析】根据二叉树的性质判定，在任意二叉树中，度为0的叶子结点总是比度为2的结点多一个。

  • 第16题：

    请教:2010年下半年软考软件设计师－上午试题(标准参考答案版)第1大题第小题如何解答?

    【题目描述】

    ● 已知一棵度为 3 的树（一个结点的度是指其子树的数目，树的度是指该树中所有结点的度的最大值）中有 5 个度为 1 的结点，4 个度为 2 的结点，2 个度为 3 的结点，那么，该树中的叶子结点数目为 （61） 。

    （61）

    A.  10          

    B.  9     

    C.  8     

    D.  7

     


    正确答案：B
    解析如下：
    设叶子节点个数为x个
    则对于树来说，所有节点度数之和等于节点个数减一
    x+5+4+2-1=5+8+6
    可得B

  • 第17题：

    某二叉树中有15个度为1的结点,16个度为2的结点,则该二叉树中总的结点数为

    A)3

    B)46

    C)48

    D)49


    正确答案：C

  • 第18题：

    设一棵二叉树中有3个叶子结点，有8个度为1的结点，则该二叉树中总的结点数为()

    A. 12

    B. 13

    C.14

    D. 15


    正确答案：B

  • 第19题：

    设一棵三叉树中有2个度数为1的结点，2个度数为2的结点，2个度数为3的结点，则该三叉链权中有()个度数为0的结点。

    A.8
    B.6
    C.7
    D.5

    答案：C
    解析：
    度为O的结点个数为1+2×1+2×2=7。

  • 第20题：

    设一棵二叉树中有3个叶子结点，有8个度为1的结点，则该二叉树中总的结点数为( )

    A.12
    B.13
    C.14
    D.15

    答案：B
    解析：

  • 第21题：

    设一棵三叉树中有2个度数为1的结点，2个度数为2的结点，2个度数为3的结点，则该三叉链权中有（）个度数为0的结点。

    • A、5
    • B、6
    • C、7
    • D、8

    正确答案:C

  • 第22题：

    已知一棵度为m的树中有：n1个度为1的结点，n2个度为2的结点，……，nm个度为m的结点，问该树中共有多少个叶子结点？


    正确答案:设该树的总结点数为n，
    则n=n0+n1+n2+……+nm
    又：n=分枝数+1=0×n0+1×n1+2×n2+……+m×nm+1由上述两式可得：
    N.0=n2+2n3+……+（m-1）nm+1

  • 第23题：

    问答题
    已知一棵度为m的树中有：n1个度为1的结点，n2个度为2的结点，……，nm个度为m的结点，问该树中共有多少个叶子结点？

    正确答案： 设该树的总结点数为n，
    则n=n0+n1+n2+……+nm
    又：n=分枝数+1=0×n0+1×n1+2×n2+……+m×nm+1由上述两式可得：
    N.0=n2+2n3+……+（m-1）nm+1
    解析： 暂无解析

相关内容