在一棵完全二叉树中,其根的序号为1,______可判定序号为p和q的两个结点是否在同一层。A.「log2p」=「log2q」B.log2p=log2qC.「log2p」+1=「log2q」D.「log2p」=「log2q」+1
题目
在一棵完全二叉树中,其根的序号为1,______可判定序号为p和q的两个结点是否在同一层。
A.「log2p」=「log2q」
B.log2p=log2q
C.「log2p」+1=「log2q」
D.「log2p」=「log2q」+1
相似考题
更多“在一棵完全二叉树中,其根的序号为1,______可判定序号为p和q的两个结点是否在同一层。A.「log2p」=「log2q」B.log2p=log2qC.「log2p」+1=「log2q」D.「log2p」=「log2q」+1”相关问题
-
第1题:
在一棵完全二叉树中,其根的序号为1,(33)可判定序号为p和q的两个结点是否在同一层。
A.
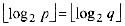
B.1og2p=log2q
C.
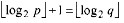
D.
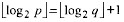 正确答案:A
正确答案:A
解析:由完全二叉树的性质可知,在一棵完全二叉树第h层(h1)上的结点p和q,它们的序号范围应是2h-1≤p,q≤2h-1,因此有 成立。
成立。
-
第2题:
● 若将某有序树 T 转换为二叉树 T1,则 T 中结点的后(根)序序列就是 T1 中结点的 (27) 遍历序列。例如下图(a)所示的有序树转化为二叉树后如图(b)所示。
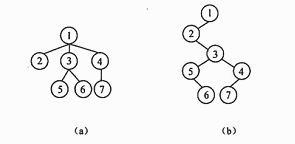
(27)
A. 先序
B. 中序
C. 后序
D. 层序
正确答案:B
-
第3题:
若对一棵有n个结点的完全二叉树的结点按层自上而下、自左至右编号,则对任意结点i(1≤i≤n),有( )。
Ⅰ.若2i>n,则结点i无左孩子
Ⅱ若2i+1>n,则结点无右孩子
Ⅲ.若结点i有左孩子,则其左孩子编号为2i
Ⅳ.若i>1,则其双亲结点编号为{i/2}
A.Ⅱ和Ⅲ
B.Ⅰ和Ⅱ
C.Ⅲ和Ⅳ
D.全都是
正确答案:D
解析:通过二叉树的基本性质可以得到以上结论。 -
第4题:
在一棵完全二叉树中,其根的序号为1,(31)可判定序号为p和q的两个结点是否在同一层。
A.[log2p]=[log2p]
B.log2p=log2q
C.[log2p]+1=[log2p]
D.[log2p]=[log2p]+1
正确答案:A
解析:同一层的结点都是2的同一倍数。 -
第5题:
在一棵二叉树结点的先根序列、中根序列和后根序列中,所有叶子结点的先后顺序【】
A.都不同相同
B.完全相同
C.先序和中序相同,而与后序不同
D.中序和后序相同,而与先序不同
正确答案:B
[解析]遍历方法中的先根、中根、后根指的是对根的访问顺序,而对于叶子结点都采用先遍历左子树,后遍历右子树. -
第6题:
对二叉树中的结点如下编号:树根结点编号为1,根的左孩子结点编号为2、右孩子结点编号为3,依此类推,对于编号为i的结点,其左孩子编号为2i、右孩子编号为2i+1。例如,下图所示二叉树中有6个结点,结点a、b、c、d、e、f的编号分别为1、2、3、5、7、11。那么,当结点数为n(n>0)的( )时,其最后一个结点编号为2i-1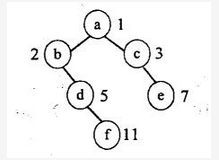 A.二叉树为满二叉树(即每层的结点数达到最大值)
A.二叉树为满二叉树(即每层的结点数达到最大值)
B.二叉树中每个内部结点都有两个孩子
C.二叉树中每个内部结点都只有左孩子
D.二叉树中每个内部结点都只有右孩子答案:C解析:本题考察二叉树的基础知识。可采用验证法。结点数为1时,只有一个结点,编号为1。结点数为2时,最后一个结点为3,那也说明只有左孩子。结点数为3时,最后一个结点编号为7。 -
第7题:
在一棵完全二叉树中,其根的序号为1,()可判定序号为p和q的两个结点是否在同一层。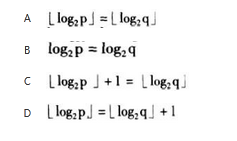 答案:A解析:
答案:A解析:
-
第8题:
对于一棵完全二叉树采用顺序存储,设一个结点的编号为i(根结点的编号为1,若它的左孩子结点存在,则其编号为()
正确答案:2i -
第9题:
将一棵有100个结点的完全二叉树从根这一层开始,每一层从左到右依次对结点进行编号,根结点编号为1,则编号为49的结点的左孩子的编号为()
- A、98
- B、99
- C、50
- D、48
正确答案:A -
第10题:
在一棵完全二叉树中,若编号为i的结点存在左孩子,则右孩子结点的编号为()
- A、2i
- B、2i+1
- C、2i+2
- D、2i-1
正确答案:B -
第11题:
单选题对一棵完全二叉树进行层序编号。则编号为n的结点若存在右孩子,其位序是()。An/2
B2n
C2n-1
D2n+1
正确答案: C解析: 暂无解析 -
第12题:
填空题对于一棵完全二叉树采用顺序存储,设一个结点的编号为i(根结点的编号为1,若它的左孩子结点存在,则其编号为()正确答案: 2i解析: 暂无解析 -
第13题:
●一棵满二叉树,其每一层结点个数都达到最大值,对其中的结点从l开始顺序编号,即根结点编号为1,其左、右孩子结点编号分别为2和3,再下一层从左到右的编号为4、5、6、7,依此类推,每一层都从左到右依次编号,直到最后的叶子结点层为止,则用 (60)可判定编号为m和n的两个结点是否在同一层。
 正确答案:B
正确答案:B
-
第14题:
在一棵完全二叉树中,其根的序号为1,(14)可判定序号为p和q的两个节点是否在同一层。
A.[logp]=[log2q)
B.log2p=log2q
C.[log2p]+1=[log2q)
D.[log2p]=[log2q)+1
正确答案:A
解析:由完全二叉树的性质可知,在一棵完全二叉树第h(h1)层上的节点p和q,它们的序号范围应是2h-1≤p,q≤2h-1,因此[logp]=[log2q)成立。 -
第15题:
在一棵完全二叉树中,其根的序号为1,(21)可判定序号为p和q的两个结点是否在同一层。
A.
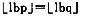
B.

C.

D.
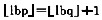 正确答案:A
正确答案:A
-
第16题:
若完全二叉树共有n个结点,且从根结点开始,按层序(每层从左到右)用正整数0,1,2,…,n-1,从小到大对结点编号,则对于编号为k的结点,错误的是______。
A.若k>0,则该结点的父结点编号为[k/2]([]表示取整)
B.若2k>n-1,则编号为k的结点无右子树,但可能有左子树
C.若2k+1<=n-1,则编号为k的结点的右子结点编号为2k+1
D.若k=0,则该结点肯定没有父结点
正确答案:B
-
第17题:
在一棵完全二叉树的顺序存储方式中,若编号为t的结点有右孩子,则此结点右孩子的编号为( )
A.2t
B.2t-1
C.2t+1
D.t/2
正确答案:C
-
第18题:
在一棵完全二叉树中,其根的序号为1,( )可判定序号为p和q的两个结点是否在同一层。A.Llog2P=Llog2q
B.log2P = log2q
C.Llog2P+1=Llog2q
D.Llog2P=+Llog2q+1答案:A解析: -
第19题:
假定一棵二叉树顺序存储在一维数组a中,但让编号为1的结点存入a[0]元素中,让编号为2的结点存入a[1]元素中,其余类推,则编号为i结点的左孩子结点对应的存储位置为(),若编号为i结点的存储位置用j表示,则其左孩子结点对应的存储位置为()。
正确答案:2i-1;2j+1 -
第20题:
对一棵完全二叉树进行层序编号。则编号为n的结点若存在右孩子,其位序是()。
- A、n/2
- B、2n
- C、2n-1
- D、2n+1
正确答案:D -
第21题:
将一棵有100个结点的完全二叉树从根这一层开始,每一层上从左到右依次对结点进行编号,根结点的编号为1,则编号为49的结点的左孩子编号为()。
- A、98
- B、99
- C、50
- D、48
正确答案:A -
第22题:
将一棵有100个结点的完全二叉树从根这一层开始,每一层从左到右依次对结点进行编号,根结点编号为1,则编号最大的非叶结点的编号为()
- A、48
- B、49
- C、50
- D、51
正确答案:C -
第23题:
单选题在一棵完全二叉树中,若编号为i的结点存在左孩子,则右孩子结点的编号为()A2i
B2i+1
C2i+2
D2i-1
正确答案: B解析: 暂无解析
