● 某公司接到一栋大楼的布线任务,经过分析决定将大楼的四层布线任务分别交给甲、乙、丙、丁四个项目经理,每人负责一层布线任务,每层面积为 10000平米。布线任务由同一个施工队施工,该工程队有5个施工组。甲经过测算,预计每个施工组每天可以铺设完成 200平米,于是估计任务完成时间为10 天,甲带领施工队最终经过14天完成任务;乙在施工前咨询了工程队中有经验的成员,经过分析之后估算时间为12天,乙带领施工队最终经过13天完成;丙参考了甲、乙施工时的情况,估算施工时间为15天,丙最终用了21天完成任务;丁将前三
题目
● 某公司接到一栋大楼的布线任务,经过分析决定将大楼的四层布线任务分别交给甲、乙、丙、丁四个项目经理,每人负责一层布线任务,每层面积为 10000平米。布线任务由同一个施工队施工,该工程队有5个施工组。甲经过测算,预计每个施工组每天可以铺设完成 200平米,于是估计任务完成时间为10 天,甲带领施工队最终经过14天完成任务;乙在施工前咨询了工程队中有经验的成员,经过分析之后估算时间为12天,乙带领施工队最终经过13天完成;丙参考了甲、乙施工时的情况,估算施工时间为15天,丙最终用了21天完成任务;丁将前三个施工队的工期代入三点估算公式计算得到估计值为 15天,最终丁带领施工队用了 15 天完成任务。以下说法正确的是(40) 。
(40)
A.甲采用的是参数估算法,参数估计不准确导致实际工期与预期有较大偏差
B.乙采用的是专家判断法,实际工期偏差只有1 天与专家的经验有很大关系
C.丙采用的是类比估算法,由于此类工程不适合采用该方法,因此偏差最大
D.丁采用的是三点估算法,工期零偏差是因为该方法是估算工期的最佳方法
相似考题
更多“● 某公司接到一栋大楼的布线任务,经过分析决定将大楼的四层布线任务分别交给甲、乙、丙、丁四个项目经理,每人负责一层布线任务,每层面积为 10000平米。布线任务由同一个施工队施工,该工程队有5个施工组。甲经过测算,预计每个施工组每天可以铺设完成 200平米,于是估计任务完成时间为10 天,甲带领施工队最终经过14天完成任务;乙在施工前咨询了工程队中有经验的成员,经过分析之后估算时间为12天,乙带领施工队最终经过13天完成;丙参考了甲、乙施工时的情况,估算施工时间为15天,丙最终用了21天完成任务;丁将前三”相关问题
-
第1题:
甲、乙、丙三个工程队在铺设两条道路,道路A长900米,道路B长1250米。已知甲、乙、丙每天分别能完成道路施工24、30、32米,甲负责道路A,丙负责道路B,乙先帮助甲铺设道路A,然后又去帮勖丙铺设道路B。两条道路同时开工同时完工,那么乙队分别帮助甲、丙两队施工多少天?( )
A.16天,20天
B.lo天,15天
C.14天,11天
D.20天,15天
正确答案:B
B[解析]道路总长度为900+1250=2150(米),每天三个施工队共可以完成24+30+32=86(米),因此共需要施工2150÷86=25(天)。甲队25天可以完成24×25=600(米),则乙队要帮甲队完成900–600=300(米)再去帮丙队,即乙队帮甲队施工300÷30=10(天)之后,又去帮丙队施工25-10=15(天)。故答案为B。 -
第2题:
某公司接到一栋大楼的布线任务,经过分析决定将大楼的4层布线任务分别交给甲、乙、丙、丁4个项目经理,每人负责一层布线任务,每层面积为10000m2。布线任务由同一个施工队施工,该工程队有5个施工组。甲经过测算,预计每个施工组每天可以铺设完成200 m2,于是估计任务完成时间为10天,甲带领施工队最终经过14天完成任务;乙在施工前咨询了工程队中有经验的成员,经过分析之后估算时间为12天,乙带领施工队最终经过13天完成;丙参考了甲、乙施工时的情况,估算施工时间为15天,丙最终用了21天完成任务;丁将前三个施工队的工期代入三点估算公式计算得到估计值为15天,最终丁带领施工队用了15天完成任务。以下说法正确的是()A.甲采用的是参数估算法,参数估计不准确导致实际工期与预期有较大偏差
B.乙采用的是专家判断法,实际工期偏差只有1天与专家的经验有很大关系
C.丙采用的是类比估算法,由于此类工程不适合采用该方法,因此偏差最大
D.丁采用的是三点估算法,工期零偏差是因为该方法是估算工期的最佳方法答案:B解析:本题考查的是活动历时估算方法问题。活动历时估算所采用的主要方法和技术如下:(1)专家判断由于影响活动持续时间的因素太多,如资源的水平或生产率,所以常常难以估算。只要有可能,就可以利用以历史信息为根据的专家判断。如果无法请到这种专家,则持续时间估计中的不确定性和风险就会增加。B是正确的。(2)类比估算持续时间类比估算就是以从前类似计划活动的实际持续时间为根据,估算将来的计划活动的持续时间。C是错误的。丙采用的是类比估算法,此类工程采用类比估算法没有不适合的问题,工期偏差的产生应该是源于施工队施工水平、质量、熟练程度、项目经理的控制能力等。(3)参数估算用要完成工作的数量乘以生产率可作为估算活动持续时间的量化依据。A不对。甲采用的确实是参数估算法,但测算不准确,导致工期偏差很大。(4)三点估算①最有可能的历时估算Tm②最乐观的历时估算To③最悲观的历时估算Tp活动历时的均值=(To 4Tm Tp)/6。因为是估算,难免有误差。三点估算法估算出的历时符合正态分布曲线,其标准差如下:(Tp-To)/6。D是不对的。工期虽然是零偏差,并不能说明此方法是最佳估算方法,只能说明三点估算法估算出的历时有偏差,但符合正态分布;项目经理进行了有效的控制,满足了工期要求。(5)后备分析项目团队可以在总的项目进度表中以“应急时间”、“时间储备”或“缓冲时间”名称增加一些时间,这种做法是承认进度风险的表现。故B是正确答案。 -
第3题:
甲乙丙三个施工队合作完成某项工程,10 天后甲施工队因为其他任务退出该工程,又过了5天,乙施工队也退出。然后丙施工队工作5天完成了剩下的工程。按照工作量付酬,结果甲施工队获得10万元,乙施工队获得30万元,丙施工队获得50万元,下列说法正确的是()。A.甲乙两个施工队合作完成该项工程只需要20天
B.丙施工队单独完成该项工程需要36天
C.丙施工队的工作效率等于甲乙两个施工队的工作效率之和
D.三个施工队中乙施工队的工作效率最高答案:B解析:由题意可知甲做了10天,乙做了15天,丙做了20天,又因为三个施工队都是按工作量付酬,则结合工作天数可知甲乙丙三个施工队的效率之比为1:2:2.5也即2:4:5,则工作总量为10X2+15X4+20X5=180,则A选项,甲乙两个施工队合作完成需要180+ (2+4) =30天,A选项错误: B选项,丙施工队单独完成需要180+5=36天,B选项正确: C选项,丙施工队工作效率不等于甲乙两个施工队效率之和,C选项错误: D选项,三个施工队中丙的效率最高,D选项错误。故本题应选B. -
第4题:
甲公司将建设工程发包给乙公司施工。甲公司与乙公司经备案的中标合同中工程造价为1 亿元,但双方私下约定的工程造价为8500 万元。经甲公司同意,乙公司将工程主体结构的施工分包给丙公司;经乙公司同意,丙公司又将其中的一部分分包给丁施工队。后整个建设工程竣工验收合格。关于本案,下列哪一说法是正确的?A.甲公司与乙公司经备案的中标合同为双方虚假行为,无效;而甲公司与乙公司私下关于工程造价为8500 万元的约定是双方真实意思的体现,有效
B.因乙公司将主体结构的施工分包给丙公司的行为经过了甲公司的同意,乙公司与丙公司之间的分包合同应认定为有效
C.因丙公司将部分工程的施工分包给丁施工队的行为经过了乙公司的同意,丙公司与丁施工队之间的分包合同应认定为有效
D.工程竣工后,甲公司拖欠工程款的,丙公司和施工队有权向甲公司主张工程款答案:D解析:①《建筑工程施工合同解释》第21 条规定:“当事人就同一建设工程另行订立的建设工程施工合同与经过备案的中标合同的实质性内容不一致的,应当以备案的中标合同作为结算工程价款的依据”。据此,A 选项错误;②被分包的工程不能是承包人承包的主体工程,将自己承包工程的主体结构分包给第三人的,违法分包合同无效,B 选项错误;③分包人将其分包的工程再分包的,分包合同无效,C 选项错误;④建设工程施工合同无效,但建设工程经竣工验收合格的,根据《建筑工程施工合同解释》第26 条规定:“实际施工人以转包人、违法分包人为被告起诉的,人民法院依法受理。实际施工人以发包人为被告主张权利的,人民法院可以追加转包人或者违法分包人为本案当事人。发包人只在欠付工程价款范围内对实际施工人承担责任”。因此,D 选项正确。 -
第5题:
某车间产品装配组有甲、乙、丙、丁四位员工,现有A、B、C、D四项任务,在现有生产技术及组织条件下,每位员工完成每项工作所需要的工时如下表所示。请运用匈牙利法求出员工与任务的最佳分派方案,以保证完成任务的总时间最短,并求出完成任务需要的总工时。
表每位员工完成四项工作任务的工时统计表
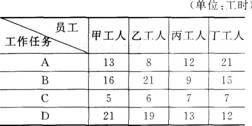 答案:解析:计算步骤如下: (1)以各个员工完成各项任务的时间建立矩阵一。
答案:解析:计算步骤如下: (1)以各个员工完成各项任务的时间建立矩阵一。

(2)对矩阵一进行约减,即每一行数据减去本行数据中的最小数,得矩阵二。

(3)检查矩阵二,发现矩阵二中各行各列均:有“0”,因此进入第四步,画“盖0”线,即画最少的线将矩阵二中的“0”全部覆盖住,得矩阵三。:

(4)检查矩阵三,发现矩阵三中“盖0”线的数目等于矩阵的维数,因此进行下列操作:找出只含有一个“0”的行(或列),将该行(或:列)中的“0”打“√”,得矩阵四。

(5)由此,我们可以看出甲负责任务C,乙负 责任务A,丙负责任务B,丁负责任务D。
(6)完成任务的总工时=5+8+9+12=34(小时) -
第6题:
甲施工队每天能完成某项工程的1/9,乙施工队施工效率是甲施工队的两倍。则甲、乙两队共同施工( )天就能完成该工程。A.2
B.3
C.4
D.5答案:B解析:第一步,本题考查工程问题,属于效率类。
第二步,赋值甲队的效率是1,则工程的总量是9,乙队的效率为2。两队一起合作完成需要9÷(1+2)=3(天)。
因此,选择B选项。 -
第7题:
甲乙丙丁四个建筑队分别承担相同的施工任务。由于设备原因,当甲乙丙同时开工时,丁已经干了若干天。经过一番努力,甲用3天,乙用5天,丙用8天,赶上了丁的进度。已知甲的效率是12,乙的效率是8,则丙的效率是( )。 答案:C解析:第一步,本题考查工程问题,用方程法解题。
答案:C解析:第一步,本题考查工程问题,用方程法解题。
第二步,设甲乙丙开工时,丁已经完成x,根据题意有(12-丁)×3=x;(8-丁)×5=x,解得丁=2,x=30。丙用了8天赶上进度,故(丙-2)×8=30,得丙=
因此,选择C选项。 -
第8题:
某工程由甲、乙两工程队合作需要10天完成,乙、丙两个工程队合作需要7天完成,甲、乙、丙三个工程队合作需要5天完成。现甲、乙、丙三个工程队同时工作,2天后,乙工程队因有其他任务撤离该工程,问甲、丙两个工程队还需多少天能完成该工程?( )A.3
B.4
C.5
D.6答案:B解析:设工程总量为70,则甲的效率+乙的效率=70÷10=7,乙的效率+丙的效率=70÷7=10,甲的效率+乙的效率+丙的效率=70÷5=14,则甲的效率=14-10=4,丙的效率=14-7=7。甲、乙、丙前两天共同完成的工作量=14×2=28,剩余工作量=70-28=42。甲、丙同时完成剩余工作量需要天数=42÷(4+7)≈3.8(天),故答案为B。 -
第9题:
某车间产品装配组有甲、乙、丙、丁四位员工,现有A、B、C、D四项任务,在现有生产技术及组织条件下,每位员工完成每项工作所需要的工时如表1所示。请运用匈牙利法求出员工与任务的最佳分配方案,以保证完成任务的总时间最短,并求出完成任务需要的总工时。? 答案:解析:具体计算过程如下:
答案:解析:具体计算过程如下:
(1)以各个员工完成各项工作的时间构造矩阵,得到矩阵一。
(注:“盖0”线的画法不唯一,如上述情况,可以画横线,也可以画竖线)
说明:由于①进行约减时,可以进行行约减,也可以进行列约减;②“盖0”线的画法不唯一。因此,计算过程不唯一,最终矩阵的形式也不唯一。但是,最终的配置结果相同。
(4)求最优解。
①找只含一个“0”的行或列,将其打√。
②将其对应的行或列的其他“0”打×。
求解结果如矩阵四所示,即工人甲负责任务C,工人乙负责任务A,工人丙负责任务B,工人丁负责任务D,参照表2—2员工完成任务时间汇总表,得出表2—3所示的员工配置最终结果。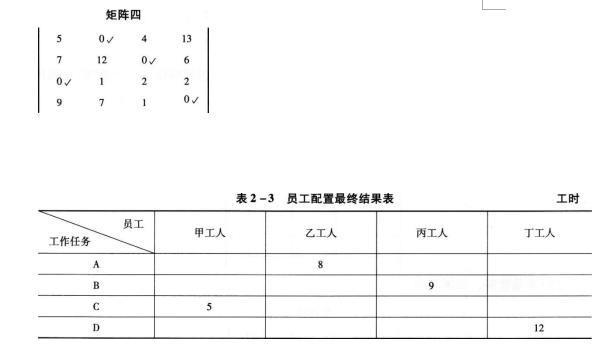
即:甲、乙、丙、丁四位员工完成任务需要的总工时为:5+8+9+12=34(工时)。 -
第10题:
甲公司把 A、B两栋楼工程发包给乙公司施工,乙公司私下把 B楼的施工任务转包给丙公司,丙公司又把 B楼的外装修工程分包给丁施工队完成。工程完工后甲公司付清了乙公司工程款,但是丁施工队没有拿到工程款,准备起诉。下面的说法中,不正确的是()。A.丁施工队是 B楼外装修工程的实际施工人
B.甲公司没把工程款给实际施工人,应当承担还款责任
C.丁施工队可以起诉丙公司、乙公司及甲公司
D.丁施工队只可以起诉丙公司答案:D解析: -
第11题:
单选题某项目组成了甲、乙、丙、丁共四个专业队进行等节奏流水施工,流水节拍为6周,最后一个专业队(丁队)从进场到完成各施工段的施工共需30周。根据分析,乙与甲、丙与乙之间各需2周技术间歇,而经过合理组织,丁对丙可插入3周进场,该项目总工期为( )周。A49
B51
C55
D56
正确答案: C解析: -
第12题:
甲、乙、丙3人植树,甲植1棵树的时间乙可植2棵,丙可植3棵,他们先一起工作5天完成全部任务的1/3,然后丙休8天,乙休3天,甲没休,最后一起完成任务,问:从开始植树算起共用多少天才完成任务?丙植树占全部任务的几分之几?()
A.20.40%
B.20.30%
C.15.30%
D.15,40%
正确答案:A

-
第13题:
施工单位甲以施工总承包方式承揽了建设单位乙的新建住院大楼项目施工任务,并将桩基工程、幕墙工程分别分包给了施工单位丙和施工单位丁。则该项目的施工安全由( )总负责。A.甲
B.乙
C.甲、丙、丁
D.甲、乙、丙、丁答案:A解析:考核施工单位的安全责任。建设工程实行施工总承包的,由总包单位对施工现场的安全生产负总责。总承包单位依法将建设工程分包给其他单位的,分包合同中应当明确各自的安全生产方面的权利、义务。总承包单位和分包单位对分包工程的安全生产承担连带责任。 -
第14题:
(2017年)甲企业为某工程项目的施工总承包方,乙企业为甲企业依法选定的分包方,丙企业为业主 依法选定的专业分包方。则关于甲、乙、丙企业在施工及管理中关系的说法,正确的是( )。A.甲企业只负责完成自己承担的施工任务
B.丙企业只听从业主的指令
C.丙企业只听从乙企业的指令
D.甲企业负责组织和管理乙企业与丙企业的施工答案:D解析:施工总承包方是工程施工的总执行者和总组织者,它除了完成自己承担的施工任务以外,还负责组织和指挥它自行分包的分包施工单位和业主指定的分包施工单位的施工。 -
第15题:
甲公司将建筑工程发包给乙公司,乙公司将其转包给丙公司,丙公司将部分工程包给由农民工组成的施工队。施工期间,丙公司拖欠施工队工程款达500万元之多,农民工因此踏上维权之路。丙公司以乙公司拖欠其工程款800万元为由、乙公司以甲公司拖欠其工程款1000万元为由均拒付欠款。施工队将甲公司诉至法院,要求甲公司支付500万元。关于本案的处理,下列哪种说法是正确的?()A:法院应驳回施工队的诉讼请求,因甲公司与施工队无合同关系
B:法院应支持施工队的诉讼请求,因为甲公司与乙公司、丙公司对施工队承担连带责任
C:法院应当追加乙公司和丙公司为本案当事人
D:法院可以追加乙公司和丙公司为本案当事人答案:D解析:最高人民法院《关于审理建设工程施工合同纠纷案件适用法律问题的解释》第26条第2款规定:“实际施工人以发包人为被告主张权利的,人民法院可以追加转包人或者违法分包人为本案当事人。发包人只在欠付工程价款范围内对实际施工人承担责任。”据此,在建设工程合同中,法律突破了合同的相对性,允许实际施工人以发包人为被告索要工程款,目的正是为了保护农民工的利益。所以,A项错误。法律突破合同的相对性,不等于要求甲公司、乙公司、丙公司对施工队承担连带责任,B项没有法律依据,错误。在突破合同相对性时,法院可以而不是应当追加转包人或者违法分包人为被告,故C项错误,D项正确。 -
第16题:
一项工程如果交给甲、乙两队共同施工,8天能完成;如果交给甲、丙两队共同施工,10天能完成;如果交给甲、丁两队共同施工,15天能完成;如果交给乙、丙、丁三队共同施工,6天就可以完成。如果甲队独立施工,需要多少天完成?( )A. 16
B. 20
C. 24
D. 28答案:C解析:8,10,15和6的最小公倍数为120,故假定这项工程的工作量为120,甲队每天的工作量为x,则有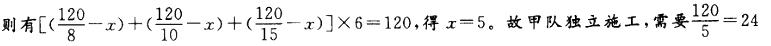 (天)完成。选C。
(天)完成。选C。 -
第17题:
甲企业为某工程项目的施工总承包方,乙企业为甲企业自行分包的分包单位,丙企业则为该工程项目业主指定的分包单位,这三家企业在施工及管理中的正确关系是()。A、 甲企业只负责完成自己承担的施工任务
B、 丙企业只听从业主的指令
C、 丙企业可指挥乙企业的施工
D、 甲企业负责组织和指挥乙企业与丙企业的施工答案:D解析:2018新教材P6 ; 不论是业主选定的分包方,或经业主授权由施工部承包管理方选定的分包方,施工总承包管理方都承担对其的组织和管理责任 -
第18题:
某项工程由甲、乙、丙三个工程队负责施工,他们将工程总量等额分成了三份同时开始施工。当乙队完成了自己任务的一半时,甲队派出一半的人力加入丙队工作。最后三队同时完成任务。则甲、乙、丙三队的施工速度比为:
A.3∶2∶1
B.4∶2∶1
C.4∶3∶2
D.6∶3∶2答案:C解析:设甲、乙、丙三个施工队满员时的施工效率分别为x、y、z,完成任务时的施工时间为1,则有(x/2)×1+(x/2)×(1/2)=y×1=z×1+(x/2)×(1/2),得x∶y∶z=4∶3∶2。 -
第19题:
甲、乙、丙、丁等4人去完成四项任务,并要求每人只完成一项任务,每一项任务只能由一人完成,每人完成各项任务的所用时间(单位:小时)如下表:
则最优分配方案是:A.甲-任务Ⅰ,乙-任务Ⅱ,丙-任务Ⅳ,丁-任务Ⅲ
B.甲-任务Ⅰ,乙-任务Ⅲ,丙-任务Ⅱ,丁-任务Ⅳ
C.甲-任务Ⅳ,乙-任务Ⅱ,丙-任务Ⅲ,丁-任务Ⅰ
D.甲-任务Ⅰ,乙-任务Ⅲ,丙-任务Ⅳ,丁-任务Ⅱ答案:D解析:要想最优方案,则所有人尽量按效率高的来分工,观察题目表格与选项差别,对于甲最适合的任务是Ⅰ,排除C;对于丙,最合适的是任务Ⅳ,排除B,任务Ⅱ与任务Ⅲ,对于乙和丁,其中乙干任务Ⅲ、丁干任务Ⅱ更优化。因此,选择D选项。 -
第20题:
某车间产品装配组有甲、乙、丙、丁四名员工,现有A、B、C三项任务需要完成,在现有生产技术组织条件下,每位员工完成每项工作所需要的工时如表1所示。
表1 四名员工完成3项任务的工时统计表 单位为工时
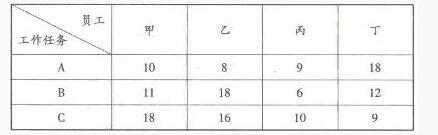
请运用匈牙利法求出员工与任务的配置方法,以保证完成任务的总时间最短,并求出完成任务的最短时间。(18分)答案:解析:(P115-120)四名员工负责三项任务,则必须有一名员工没有任务,此时可增添一项虚拟任务D,各员工完成任务D的时间均为0,表1变形为表2,如下:
表2四名员工完成任务的工时统计表 单位为工时
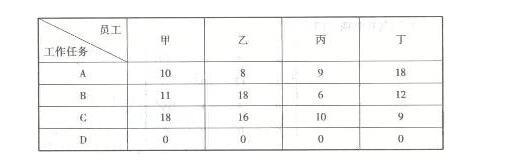
此时,可利用匈牙利法。(2分)
(1)根据表2,构造矩阵一。(3分)

(2)对矩阵一进行行约减,即每一行数据减去本行数据中的最小数,得矩阵二。(2分)

(3)检查矩阵二,发现矩阵二中各行各列均有“0”,因此进入第四步,画“盖0”线,即画最少的线将矩阵二中的“0”全部覆盖住,得矩阵三。(3分)
(4)检查矩阵三,发现矩阵三中“盖0”线的数目等于矩阵的维数,因此进行下列操作:找出只含有一个“0”的行(或列),将该行(或列)中的“0”打“√”,得矩阵四。(3分)

(5)由此,我们可以看出乙负责任务A,丙负责任务B,丁负责任务C,如表3所示:(3分)
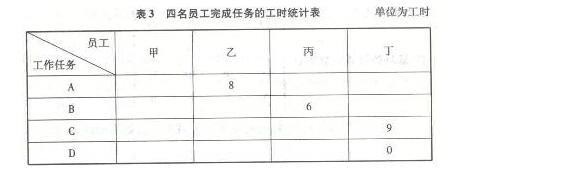
(6)完成任务的总工时数=8+6+9=23(小时)。(2分) -
第21题:
甲企业为某工程项目的施工总承包方,乙企业为甲企业依法选定的分包方,丙企业为业主依法选定的专业分包方。则关于甲、乙、丙企业在施工及管理中关系的说法,正确的是()。
- A、甲企业只负责完成自己承担的施工任务
- B、丙企业只听从业主的指令
- C、丙企业只听从乙企业的指令
- D、甲企业负责组织和管理乙企业与丙企业的施工
正确答案:D
