itgle.com

当运用改进的模式匹配算法时，模式串P='ABAABCAC'的next函数值序列为(41)。A．1222312B．1122312C．1122212D．122312

题目

当运用改进的模式匹配算法时，模式串P='ABAABCAC'的next函数值序列为(41)。

A．1222312

B．1122312

C．1122212

D．122312

相似考题

1.设有两个串p和q，求q在p中首次出现位置的运算称作A．连接B．模式匹配C．求子串D．求串长

2.设有两个串p和q,其中q是p的子串,求q在p中首次出现的位置的算法称为( )。A、求子串B、联接C、模式匹配D、求串长

3.设目标为t=“abcaabbabcabaacbacba”,模式为p=“abcabaa” ① 计算模式p的naxtval函数值; ② 不写出算法,只画出利用KMP算法进行模式匹配时每一趟的匹配过程。

4.●在字符串的模式匹配过程中，如果模式串的每个字符依次和主事中一个连续的字符序列相等，则称为匹配成功。如果不能在主串中找到与模式串相同的子串，则称为匹配失败。在布鲁特—福斯模式匹配算法（朴素的或基本的模式匹配）中，若主串和模式串的长度分别为n和m（且n远大于m），且恰好在主串末尾的m个字符处匹配成功，则在上述的模式匹配过程中,字符的比较次数最多为(57)。(57) A. n*mB. (n-m+1)*mC. (n-m-1)*mD. (n-m)*n

更多“当运用改进的模式匹配算法时，模式串P='ABAABCAC'的next函数值序列为(41)。A．1222312B．1122312C．1122212D．122312”相关问题

  • 第1题：

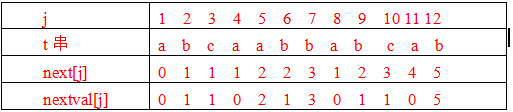
    已知模式串t=‘abcaabbabcab’写出用KMP法求得的每个字符对应的next和nextval函数值。


    参考答案：
    　　模式串t的next和nextval值如下：
    　　

  • 第2题：

    设主串长为n，模式串长为m(m≤n)，则在匹配失败情况下，朴素匹配算法进行的无效位移次数为 ( )

    A．m

    B．n-m

    C．n-m+1

    D．n


    正确答案：C

  • 第3题：

    若目标串的长度为n，模式串的长度为[n/3]，则执行模式匹配算法时，在最坏情况下的时间复杂度是( )。

    A．O(1)

    B．O(n)

    C．O(n2)

    D．0(n3)


    正确答案：C
    解析：在主串中可能存在多个模式串“部分匹配”的子串，因而引起数次回溯，若除了最后一次匹配，其他比较每次都需要回溯，则循环次数的数量级为n2。

  • 第4题：

    在字符串的KMP模式匹配算法中，需先求解模式串的next函数值，其定义如下式所示，j表示模式串中字符的序号（从1开始）。若模式串p为"abaac"，则其next函数值为 （ ） 。

    A.01234
    B.01122
    C.01211
    D.01111

    答案：B
    解析：
    根据公式依次推导即可。

  • 第5题：

    在字符串的KMP模式匹配算法中，需先求解模式串的next函数值，其定义如下式所示，j表示模式串中字符的序号（从1开始）。若模式串p为"abaac"，则其next函数值为（60）。


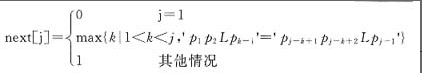    A.01234
    B.01122
    C.01211
    D.01111

    答案：B
    解析：
    根据公式依次推导即可。

  • 第6题：

    KMP模式匹配算法的改进之处是（）。

    • A、主串指针不需要回溯
    • B、模式串的指针来回移动
    • C、主串的指针也会回到之前比较过的字符
    • D、时间复杂度可以达到O（nm）

    正确答案:A

  • 第7题：

    子串的定位运算称为串的模式匹配；（）称为目标串，（）称为模式。


    正确答案:被匹配的主串 子串

  • 第8题：

    模式串T=’abcaabbcabcaabdab’，该模式串的next数组值为（），nexrval数组的值为（）


    正确答案:01112231123456712；01102131011021701

  • 第9题：

    填空题
    写出模式串P=“abaabcac”的next函数值序列为（）。

    正确答案： 01122312
    解析： 暂无解析

  • 第10题：

    填空题
    子串的定位运算称为串的模式匹配；（）称为目标串，（）称为模式。

    正确答案： 被匹配的主串 子串
    解析： 暂无解析

  • 第11题：

    单选题
    设有两个串p 和q，求p 在q中首次出现的位置的运算称作（）。
    A

    连接

    B

    求子串

    C

    模式匹配

    D

    求串长


    正确答案： A
    解析： 暂无解析

  • 第12题：

    填空题
    模式串t=‘abcaabbcabcaabdab’，该模式串的next数组的值为（），nextval数组的值为（）

    正确答案： 01112231123456712,01102131011021701
    解析： 暂无解析

  • 第13题：

    ●在KMP模式匹配算法中，需要求解模式串p的next函数值，其定义如下（其中，j为模式串中字符的序号）。对于模式串“abaabaca”，其next函数值序列为(57)。

    (57)

    A. 01111111

    B.01122341

    C.01234567

    D.01122334


    正确答案：B

  • 第14题：

    ● 在字符串的模式匹配过程中，如果模式串的每个字符依次和主事中一个连续的字符序列相等，则称为匹配成功。如果不能在主串中找到与模式串相同的子串，则称为匹配失败。在布鲁特—福斯模式匹配算法（朴素的或基本的模式匹配）中，若主串和模式串的长度分别为n和m（且n远大于m），且恰好在主串末尾的m个字符处匹配成功，则在上述的模式匹配过程中，字符的比较次数最多为（57）。 A.n*m B.（n-m+1）*m C.（n-m-1）*m D.（n-m）*n


    正确答案：B
    试题57分析本题主要考查字符串的匹配。在本题的描述中，告诉我们是在主串末尾的m个字符处匹配成功，那么在这之前，从左到右依次匹配了n-m次，且都失败了，最坏的情况，就是每次匹配都是匹配到最后一个字符不符合，因此每次匹配的比较次数就是子串的长度，即m。而匹配成功时，一共也比较了m次。所以字符的比较次数最多为（n-m+1）*m次。参考答案（57）B

  • 第15题：

    设有两个串P和q，求q在P中首次出现的位置的运算称作______。

    A．连接

    B．模式匹配

    C．求子串

    D．求串长


    正确答案：B
    解析：求一个串在另一个串中首次出现的位置的运算称作模式匹配。

  • 第16题：

    KMP算法的特点是在模式匹配时指示主串的指针()。

    A.不会变大
    B.不会变小
    C.都有可能
    D.无法判断

    答案：B
    解析：
    在KMP算法中，模式匹配时主串不会回溯，所以主串的指针不会变小。

  • 第17题：

    KMP算法的特点是在模式匹配时指示主串的指针不会回溯。


    正确答案:正确

  • 第18题：

    设有两个串p和q，求q在p中首次出现的位置的运算称作（）

    • A、连接
    • B、模式匹配
    • C、求子串
    • D、求串长

    正确答案:B

  • 第19题：

    模式串t=‘abcaabbcabcaabdab’，该模式串的next数组的值为（），nextval数组的值为（）


    正确答案:01112231123456712；01102131011021701

  • 第20题：

    写出模式串P=“abaabcac”的next函数值序列为（）。


    正确答案:01122312

  • 第21题：

    填空题
    模式串T=’abcaabbcabcaabdab’，该模式串的next数组值为（），nexrval数组的值为（）

    正确答案： 01112231123456712,01102131011021701
    解析： 暂无解析

  • 第22题：

    判断题
    KMP算法的特点是在模式匹配时指示主串的指针不会回溯。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第23题：

    单选题
    KMP模式匹配算法的改进之处是（）。
    A

    主串指针不需要回溯

    B

    模式串的指针来回移动

    C

    主串的指针也会回到之前比较过的字符

    D

    时间复杂度可以达到O（nm）


    正确答案： D
    解析： 暂无解析

相关内容