一个袋子里装有三种不同颜色但大小相同的小球。红色小球上标有数字1,黄色小球上标有数字2,蓝色小球上标有数字3。小明从袋中摸出10个小球,它们的数字和是21,那么小明摸出的小球中最多可能有多少个小球是红色的?( )A.3个B.4个C.5个D.6个
题目
一个袋子里装有三种不同颜色但大小相同的小球。红色小球上标有数字1,黄色小球上标有数字2,蓝色小球上标有数字3。小明从袋中摸出10个小球,它们的数字和是21,那么小明摸出的小球中最多可能有多少个小球是红色的?( )
A.3个
B.4个
C.5个
D.6个
相似考题
更多“一个袋子里装有三种不同颜色但大小相同的小球。红色小球上标有数字1,黄色小球上标有数字 ”相关问题
-
第1题:
一个袋子里面有红、黄、蓝三个颜色的小球共450个,三个颜色的小球数目比例为2:3:4,问数目连多的颜色的球有多少个?( )
A.100
B.150
C.200
D.250
正确答案:C可以把总数看做包括了2+3+4=9份,其中数目最多的肯定是占4/9的颜色球。 -
第2题:
一个袋子里放着各种颜色的小球,其中红球占 1/4。后来又往袋子里放了 10 个红球,这时红球占总数的 2/3,问原来袋子里有球多少个?( )
A.8
B.6
C.4
D.2
正确答案:A
-
第3题:
一个袋子里面有红、黄、蓝三种颜色的球共450个,三个颜色的小球数目比例为2:3:4,问数目最多的颜色的球有多少个?( )
A.100
B.150
C.200
D.250
正确答案:C
-
第4题:
12 、现有两个不透明的袋子,其中一个装有标号分别为 1 、 2 的两个小球,另一个装有标号分别为 2 、 3 、 4 的三个小球 , 小球除标号外其它均相同 , 从两个袋子中各随机摸出 1 个小球 ,两球标号恰好相同的概率是 _________ .
正确答案:考点:列表法与树状图法。
分析:首先根据题意画树状图,然后由树状图求得所有等可能的结果与两球标号恰好相同的情况,即可根据概率公式求解.
解答:解:画树状图得:
∴一共有6种等可能的结果,
两球标号恰好相同的有1种情况,
∴两球标号恰好相同的概率是1/6.
点评:此题考查了树状图法与列表法求概率.树状图法与列表法适合两步完成的事件,可以不重不漏的表示出所有等可能的情况.用到的知识点为:概率=所求情况数与总情况数之比.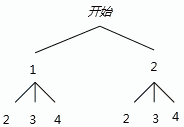
-
第5题:
一个袋子里有10个小球,其中4个白球,6个黑球,无放回地每次抽取1个,则第二次取到白球的概率是多少?( ) 答案:D解析:
答案:D解析:
-
第6题:
(7分)抽奖盒内有若干个小球,把从1开始的若干个连续奇数依次写在小球上,某顾客从抽奖中抽出一个小球,但该小球上的数字模糊不清,经统计,剩余小球上各数字的加和为1555。若抽奖规则为抽到能被3整除的数,即为中奖,请判断该名顾客是否中奖。答案:解析:设共有n个小球,则小球上的编号为l,3,5,……,2n-1,
考虑l555附近的完全平方数,不难判断n=40,小球上的数字之和为l600,顾客抽到的小球编号为l600-1555=45,故可确定该顾客中奖。 -
第7题:
一个袋子里放着各种颜色的小球,其中红球占1/4,后来又往袋子里放了10个红球,这时红球占总数的2/3,问原来袋子里有多少个球?()
A. 8
B. 12
C. 16
D. 20答案:A解析:解题指导: 设原来袋中有X个球,则一开始红球有1/4X个,根据题意可得方程1/4X+10=2/3(X+10),解得X=8,故答案选A。 -
第8题:
抽屉里有黑色小球13只,红色小球7只,现在要选3个球出来,至少要有2只红球的不同选法共有多少种?( )。
A. 308
B. 378
C. 616
D. 458答案:A解析:解题指导: C(7,2)×C(13,1)=21×13=273,C(7,3)=35,总共:273+35=308。故答案为A。 -
第9题:
一个盒子装有m(m≤100)个小球,每次按照2个、3个、4个的顺序取出,最终盒内都只剩下1个小球,如果每次取出11个,期余4个,则m的各数位上的数字之和为A.9
B.10
C.11
D.12
E.13答案:B解析:由“每次2个、3个,4个的取出,最终盒内都只刺下1个小球”知m一1能被2,3,4的最小公倍数12整除。设m=12k1+1=11k1+k1+1=11k2+4,故有k1+1=4,k1=3,故m=12k1+1=37,则m的各数位上的数字之和为10. -
第10题:
站在高高的嘹望塔上,从同一高度以大小相同的速度同时抛出三个质量相同的小球,但抛出方向各不相同,不计空气阻力,这三个小球落到同一水平面时,三个小球的速度大小是否相同?三个小球重力的功是否相同?三个小球落地的时间是否相同()。
- A、速度大小不相同
- B、重力功相同
- C、落地时间相同
- D、重力功不同
正确答案:B -
第11题:
一个盒子里中有相同大小的玻璃球共40个,其中红、黄、蓝三种颜色的玻璃球各10个,其余玻璃球的颜色未知。那么至少需要摸出()个玻璃球,才能保证取到的小球中,至少有5个小球的颜色相同?
- A、13
- B、17
- C、23
- D、24
正确答案:C -
第12题:
单选题站在高高的嘹望塔上,从同一高度以大小相同的速度同时抛出三个质量相同的小球,但抛出方向各不相同,不计空气阻力,这三个小球落到同一水平面时,三个小球的速度大小是否相同?三个小球重力的功是否相同?三个小球落地的时间是否相同()。A速度大小不相同
B重力功相同
C落地时间相同
D重力功不同
正确答案: C解析: 暂无解析 -
第13题:
一个袋子里装了各种颜色的小球,其中红球个数占1/4,后来又向袋子中放入10个红球,这时红球个数占总数的2/3,问原来袋子中共有多少球?
设原来有总数有X个小球,所以(X/4+10)/(X+10)=2/3
解方程得X=8 -
第14题:
盒子中装了大球和小球,颜色分别有红色和白色。大球中红球占80%,小球中红球占602,在整个盒子里红球占62%,红色大球与白色小球数目之比是( )。
A.1:9
B.9:1
C.2:9
D.9:2
正确答案:C
-
第15题:
抽屉里有黑色小球13只,红色小球2只,现在要选3个球出来,至少要有2只红球的不同选法共有多少种?( )。
A.308
B.378
C.616
D.458
正确答案:A
-
第16题:
在一只暗箱里有黑色的小球30只,白色的小球22只,蓝色的小球18只,大小都一样,每摸出两个同色小球奖励1分,从暗箱中至少摸出多少只小球才能保证至少得10分:
A30
B18
C20
D22答案:D解析:解析:
得10分,即摸到了10对颜色相同的小球。考虑最差的情况,当摸到了9对颜色相同的小球后,又各摸出3个颜色不同的小球,此时只需要再摸出任意颜色小球一个,即可保证有10对颜色相同的小球。
所以至少摸出小球是9*2+3+1=22个。故正确答案为D。 -
第17题:
有6种颜色的小球,数量分别为4,6,8,9,11,10,将它们放在一个盒子里,那么,拿到相同颜色的球最多需要的次数为:A.6
B.12
C.11
D.7答案:D解析:第一步,本题考查最值问题,属于最不利构造。
第二步,拿到相同颜色的球需要的次数最多,考虑最不利情况,即每种颜色的球各取一个,需要6次。此时再任取1球,则该球的颜色必然和之前已经取到的某个球颜色相同,最多需要6+1=7(次)。 -
第18题:
在一个袋中,装有五个除数字外其他完全相同的小球,球面上分别标有1、2、3、4、5这5个数字,从中任摸一个球,球面数字是奇数的概率是________.答案:解析: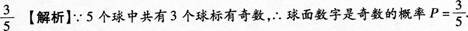
-
第19题:
数学运算。在这部分试题中,每道试题呈现一段表述数字关系的文字.要求你迅速、准确地计算出答案。
64个小球放到18个盒子里,每个里面最多放6个.所有盒子里都有小球,问最少几个盒子里的小球数目相同?()
A.2
B.3
C.4
D.5答案:C解析:利用抽屉原理,按题干要求每个盒子里都有小球。最多放6个。可以从1到6构造6个抽屉,则问题转化为至少有几个含小球数目相同的盒子在同一个抽屉里。因为共有18个盒子.18+6:3。故假设每个抽屉里有3个盒子的小球数目是相同的,故18个盒子里放的小球最多有3×(1+2+3+4+5+6)=63 -
第20题:
甲坛有8个小球,乙坛有4个小球,所有小球颜色各不相同,现从甲坛中取2个小球,乙坛中取1个小球,则取出3个球的不同取法共有()A.224种
B.112种
C.32种
D.1320种答案:B解析: -
第21题:
用初乳测定仪对初乳的质量进行测定,初乳检测仪上标明绿、黄和红色三种颜色段,()表示劣质,不能使用。
- A、红色;
- B、黄色;
- C、绿色;
- D、绿色和红色。
正确答案:A -
第22题:
有红,黄,蓝三种颜色的小球各20个,装在一只不透光的袋子里,小李伸手进袋子里面每次任意摸出一个小球。为了保证摸出三个颜色相同的小球,小李应至少摸几次?()
- A、9
- B、8
- C、7
- D、6
正确答案:C -
第23题:
单选题一个口袋内装有5个小球,另一个口袋内装有4个小球,所有这些小球的颜色互不相同.从两个口袋内任取一个小球,不同的取法有( ).A20种
B9种
C5种
D4种
正确答案: C解析:
本题为组合问题,共有5+4=9种不同的取法.
