若一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的面积增加了多少?A.100cm2 B400cm2 C.500cm2 D.600cm2
题目
若一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的面积增加了多少?
A.100cm2 B400cm2 C.500cm2 D.600cm2
相似考题
参考答案和解析
正确答案:D
正方体6个面,增加的面积为以大正方体边长为长,一小正方体边长为宽的四个面,即:20*10*4=800cm2,减少的为两个以小正方体的面:10*10*2=200cm2,所以增加的面积为800-200=600cm2
正方体6个面,增加的面积为以大正方体边长为长,一小正方体边长为宽的四个面,即:20*10*4=800cm2,减少的为两个以小正方体的面:10*10*2=200cm2,所以增加的面积为800-200=600cm2
更多“若一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的面积增加了多少 ”相关问题
-
第1题:
有64个边长为l厘米的同样大小的小正方体, 其中34个为白色的,30个为黑色的。现将它们拼成一个4×4×4的大正方体, 在大正方体的表面上白色部分最多可以是多少平方厘米?( )
A.52
B.64
C.72
D.74
正确答案:D
-
第2题:
210个边长为1厘米的小正方体组成的长方体,其表面积最小为多少?( )A.
B.
C.
D. 答案:A解析:该长方体体积为210立方厘米,根据体积一定的情况下越接近球体表面积越小,则其长、宽、高应尽量接近。210=2×3×5×7,当三个棱长分别为5、6、7时,表面积最小是2×(5×6+5×7+6×7)=214平方厘米。
答案:A解析:该长方体体积为210立方厘米,根据体积一定的情况下越接近球体表面积越小,则其长、宽、高应尽量接近。210=2×3×5×7,当三个棱长分别为5、6、7时,表面积最小是2×(5×6+5×7+6×7)=214平方厘米。 -
第3题:
1000个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体,大正方体表面涂油漆后,再分开为原来的小正方体,这些小正方体至少有一面被油漆涂过的数目是多少个:
A 490
B 488
C 484
D 480答案:B解析:
-
第4题:
将1000个边长为1cm的小正方体组合成一个实心的大正方体后,将该正方体的5个面涂满色后再全部分开,那么至少有一面涂色的小正方体有多少个?A.424
B.488
C.512
D.576答案:A解析:解法一:
第一步,本题考查几何问题,属于立体几何类。
第二步,由题意可知大正方体的边长为10cm(10^3=1000),此正方体外表面5个面涂满色,则被涂色小正方体侧面有10×(4×10-4)=360(个),底面有8×8=64(个),共有360+64=424(个)。
因此,选择A选项。
解法二:
第一步,本题考查几何问题,属于立体几何类。
第二步,由题意可知大正方体的边长为10cm(10^3=1000),未被涂色小正方体为(8×8×9)-(8×8)=8×8×9=576(个),被涂色的小正方体有1000-576=424(个)。 -
第5题:
若一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体,问大正方体的面积增加了多少?
A. 100cm2
B. 400cm2
C. 500cm2
D. 600cm2答案:B解析:小正方体里面的面积是5个面,5*10*10=500,从大正方体表面挖下去的这个面要减掉,也就是500-10*10=400. -
第6题:
连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米,问正八面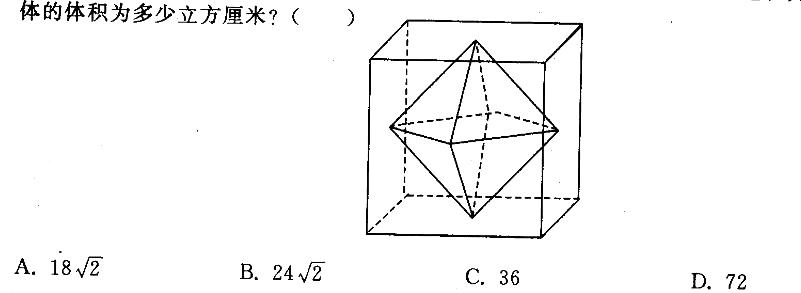 答案:C解析:该正八面体可以看做由两个四棱锥拼成的,每个四棱锥的底面为原正方体四个侧面的中心连线,高分别为上下两个正方体底面中心到四棱锥底面的距离,解得V= 1/3x(62x1/2)X3X2 =36(cm3)。
答案:C解析:该正八面体可以看做由两个四棱锥拼成的,每个四棱锥的底面为原正方体四个侧面的中心连线,高分别为上下两个正方体底面中心到四棱锥底面的距离,解得V= 1/3x(62x1/2)X3X2 =36(cm3)。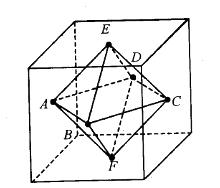
-
第7题:
边长为4的正方体木块,各面均涂成红色,将其锯成64个边长为1的小正方体,并将它们搅匀混在一起,随机抽取一个小正方体,恰有两面为红色的概率是( )
 答案:A解析:锯成64个边长为1的小正方体后,涂色的面有以下几种情况:涂3面的小正方体分别在大正方体的8个顶点处,共有8个;涂2面的小正方体分别是大正方体的每条棱的中间的2个,而大正方体共有12条棱,那么,涂2面的小正方体有2×12=24个;涂1面的小正方体分别是每个面的中间的4个,而大正方体共有6个面,那么,涂1面的小正方体有4×6=24个;6个面都没有涂色的小正方体有64-8-24-24=8个,则随机抽取一个小正方体,恰有两面为红色的概率是
答案:A解析:锯成64个边长为1的小正方体后,涂色的面有以下几种情况:涂3面的小正方体分别在大正方体的8个顶点处,共有8个;涂2面的小正方体分别是大正方体的每条棱的中间的2个,而大正方体共有12条棱,那么,涂2面的小正方体有2×12=24个;涂1面的小正方体分别是每个面的中间的4个,而大正方体共有6个面,那么,涂1面的小正方体有4×6=24个;6个面都没有涂色的小正方体有64-8-24-24=8个,则随机抽取一个小正方体,恰有两面为红色的概率是

-
第8题:
单选题连接正方体每个面的中心构成一个正八面体。己知正方体的边长为6厘米,问正八面体的体积为多少立方厘米?()A182
B242
C36
D72
正确答案: C解析: 暂无解析 -
第9题:
单选题若在一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的表面积增加了多少?( )A100cm2
B400cm2
C500cm2
D600cm2
正确答案: C解析:
在一个边长为20cm的大正方体中挖去一个边长为10cm的小正方体,则大正方体原有的6个面只有其中一个面的面积减少了100cm2,而小正方体则多出了5个100cm2的面,因此大正方体的面积增加了400cm2。 -
第10题:
若一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的表面积增加了多少?( ) A.100 cm2 B.400 cm2 C.500 cm2 D.600 cm2
正确答案:B
本题属于几何问题。在正方体表面挖出一个10Cm正方体后,大正方体增加的表面积实际上为挖出小正方体的四个面面积,该面积为102X4=400Cm2。故选B。
-
第11题:
一只蚂蚁从右图的正方体的A顶点沿正方体的表面爬到正方体的C顶点,设正方体边长为a,问该蚂蚁爬过的最短路程为:
 答案:B解析:
答案:B解析: -
第12题:
边长为6的正方体,由若干个边长为1的正方体组成,现将大正方体表面涂上色,请问仅有一面着色的小正方体与仅有两面着色的小正方体个数之差为多少?A.36
B.48
C.54
D.64答案:B解析:本题属于几何问题。
正方体六面八个顶点十二条棱。仅有两面着色的是每条棱上的4个小正方体,总计4×12=48个;仅有一面着色的是每个面中间的4×4=16个正方体,六个面总共有=4×4×6=96个;故个数之差=96-48=48,B选项正确。
因此,选择B选项。 -
第13题:
一只蚂蚁从右图的正方体的A顶点沿正方体的表面爬到正方体的C顶点,设正方体边长为a,问该蚂蚁爬过的最短路程为: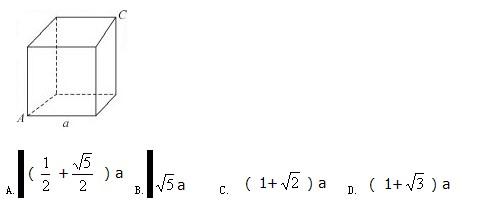
A.A B. B C. C D. D答案:B解析:解题指导: 该最短路程为√[1+﹙22a﹚]=√5a。故答案为B。 -
第14题:
一千个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体,大正方体表面涂油漆后再分开为原来的小正方体,这些小正方体至少有一面被油漆涂过的数目是( )个。A.490
B.488
C.484
D.480答案:B解析:分析:没有涂色的小正方体都在大正方体的内部,由此先借助正方体的体积公式求出没有涂色的小正方体的个数即可解答.
解答:解:没有涂色的小正方体:
(10-2)×(10-2)×(10-2)=8×8×8=512(个),
所以至少一面涂色的小正方体:1000-512=488(个) -
第15题:
连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘 米,问正八面体的体积为多少立方厘米?( )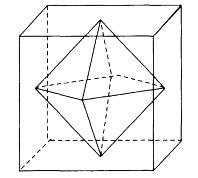
 答案:C解析:
答案:C解析:
-
第16题:
连接正方体每个面的中心构成一个正八面体。己知正方体的边长为6厘米,问正八面体的体积为多少立方厘米?()
- A、182
- B、242
- C、36
- D、72
正确答案:C -
第17题:
单选题若在一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的表面积增加了多少?( )A100㎝2
B400㎝2
C500㎝2
D600㎝2
正确答案: B解析:
在一个边长为20㎝的大正方体中挖去1个边长为10㎝的小正方体,则大正方体原有的6个面只有其中1个面的面积减少了100㎝2,而小正方体则多出了5个100㎝2的面,因此大正方体的面积增加了400㎝2。
