用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成最大的一个长方形面积是多少平方厘米?( )A.16B.15C.12D.9
题目
用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成最大的一个长方形面积是多少平方厘米?( )
A.16
B.15
C.12
D.9
相似考题
更多“用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成最大的一个长方形面 ”相关问题
-
第1题:
用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成的最大的一个长方形的面积是多少平方厘米?( )A. 16
B. 15
C. 12
D. 9答案:B解析:设长方形的长为a,宽为b,则这个问题就是求已知a+b=8、且a≠b时,axb的最大值。为了便于观察,我们分析如下:
8 = 1 + 7→1X7=7;8 = 2 + 6→2X6 = 12;
8 = 3 + 5→3 X5=15;8 = 4 + 4→4 X 4 = 16;
8 = 5 + 3→5X3=15;8 = 6 + 2 → 6X2 = 12;
8 = 7 + 1→ 7X1=7。
我们发现当a从小到大取值,而b从大到小取值时,a与b的积呈现这样一个变化趋势:就是先由小到大,再由大到小,中间是最大的,也就是a与b取的数越接近,它们的乘积就越大。当a = b时,aXb的值最大。由此,得出一条规律:
如果a+b—定,只有当a =b时,a与b的乘积才最大。
由上面的讨论可知,在a +b=8,且a≠b中,当a=3,b= 5时,aXb的最大值是:3X5 = 15。 所以,所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。 -
第2题:
如下图,大长方形被分为四个较小长方形,已知四个长方形的面积已标示出来,且这个大长方形的长和宽均为整数,那么图中双向箭头之间的部分是多长?( )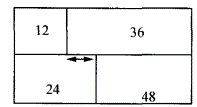 A. 1
A. 1
B. 2
C. 1 或 2
D. 3答案:C解析:
-
第3题:
22、一根长60cm的铁丝,可以围成一个长8cm,宽4cm,高()cm的长方体框架。
A.2
B.3
C.4
D.5
9 -
第4题:
用18厘米长的警戒线围成各种长方形,要求长和宽的长度都是厘米数,则围成的长方形的面积最大是多少?A.18平方厘米
B.20平方厘米
C.25平方厘米
D.40平方厘米答案:B解析:第一步,本题考查几何问题,属于几何特殊性质类。
第二步,由题意知长+宽=9厘米,要使长方形的面积尽可能大,则要求长和宽尽量接近,可使长=5厘米,宽=4厘米,此时面积最大,最大面积为4×5=20(平方厘米)。 -
第5题:
一根长60cm的铁丝,可以围成一个长8cm,宽4cm,高()cm的长方体框架。
A.2
B.3
C.4
D.5
146
