itgle.com

一个正方形的一边减少20%，另一边增加2，得到长方形的面积与原正方形的面积相等，问正方形面积是多少?A．8B．10C．16D．64

题目

一个正方形的一边减少20%，另一边增加2，得到长方形的面积与原正方形的面积相等，问正方形面积是多少?

A．8

B．10

C．16

D．64

相似考题

1.一个农夫发现围成正方形的围栏比长方形的节省4个木桩但是面积一样.羊的数目和正方形围栏的桩子的个数一样但是小于36，问有多少羊？（威盛）

2.把一个正方形的一边减少2cm，另一边增加20%，得到一个长方形，它与原来的正方形面积相等，那么，正方形的边长是( )。m。A．13B．10C．12D．15

3.一个长方形的长减少5cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等。这个长方形的长、宽各是多少

4.一个长方形，若将短边长度增加4厘米，长边长度增加一倍，则面积是原来的3倍，若将长边缩短8厘米，就成正方形，则原长方形面积是多少平方厘米?( )A．180B．128C．84D．48

参考答案和解析
正确答案：D
[答案] D。解析：设正方形的边长为x，(1-20%)×(x+2)=x2,x=8。原正方形的面积为64。
更多“一个正方形的一边减少20%，另一边增加2，得到长方形的面积与原正方形的面积相等，问正方形面积是多少?A．8B．10C．16D．64”相关问题

  • 第1题：

    将一根铁丝分别弯制成圆形 、 正方形 、 长方形 ， 问弯成哪种形状时该铁丝所围的面积最大 ?( )

    A ．圆形

    B ．正方形

    C ．长方形

    D ．一样大


    正确答案：A

    30 ． A

  • 第2题：

    将一根铁丝分别弯制成圆形、正方形、长方形，问弯成哪种形状时该铁丝所围的面积最

    大?( )

    A．圆形

    B．正方形

    C．长方形

    D．一样大


    正确答案：A

  • 第3题：

    一正方形铁片面积为1平方米，用其剪出一个最大的圆，然后再圆中剪出一个最大的正方形，问新正方形的面积比原正方形的面积小多少？

    A.1/4平方米
    B.1/2平方米
    C.π/8平方米
    D.π/16平方米

    答案：B
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，由正方形铁片面积为1平方米，可知正方形的边长是1米，切割出的新正方形的对角线为最大圆的直径，即原正方形的边长。新正方形的边长为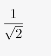


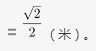
    新正方形的面积为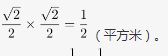

    第三步，故新正方形的面积比原正方形小了

  • 第4题：

    如图，甲，乙，丙，丁四个长方形拼成正方形EFGH,中间阴影为正方形。已知，甲、乙、丙、丁四个长方形面积的和是32cm2，四边形ABCD的面积是20cm2。问甲、乙、丙、丁四个长方形周长的总和是（）。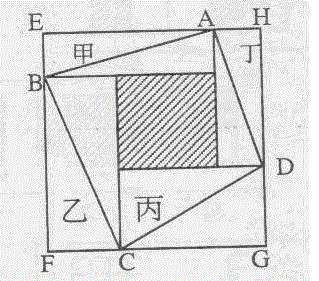


    A. 32cm
    B. 56cm
    C. 48cm
    D. 68cm

    答案：C
    解析：
    可以观察出,所求的四个长方形的周长等于四边形EFGH的周长的2倍。阴影面积=四边形ABCD的面积-四个长方形(甲、乙、丙、丁)面积的和的一半=20-16=4。 四边形EFGH的面积=四个长方形的面积+阴影面积=32+4=36,所以四边形EFGH的边长为6,周长为24。故答案为C。

  • 第5题：

    如图，有大小两个正方形，其对应边的距离均为1厘米。如果两个正方形之间部分的面积是20平方厘米，那么，小正方形的面积是多少平方厘米？（ ）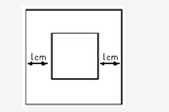


    A4
    B9
    C16
    D25


    答案：C
    解析：
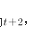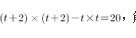    设小正方形的边长为，则大正方形的边长为，依题意有，解之得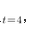，所以面积为16。

    故正确答案为C。

  • 第6题：

    某长方形长和宽的比是4:3，如果长减少4米，宽增加6米则变成一个正方形，原长方形的面积为（__）平方米？

    A. 900
    B. 1200
    C. 1500
    D. 1800

    答案：B
    解析：
    本题考查基础几何问题。设长为4x，宽为3x，4x-4=3x+6，解得x=10，则长方形长40，宽30，面积为30*40=1200

  • 第7题：

    在大小相等的两个等腰直角三角形中，按不同的方式各内接一个正方形（如图A、B所示）。如果图B中的内接正方形的面积是144，那么图A中的内接正方形的面积是多少？


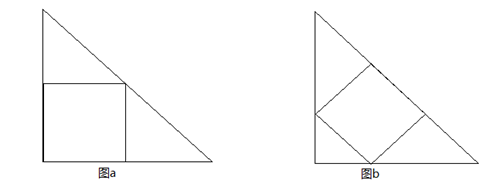    A. 225
    B. 162
    C. 128
    D. 98

    答案：B
    解析：

  • 第8题：

    图形面积相等的两个图，如：圆和正方形，在视觉上感到正方形的面积（）圆的面积。


    正确答案:大于

  • 第9题：

    面积相等的图形中下列图形周长最短的是（）

    • A、圆
    • B、三角形
    • C、长方形
    • D、正方形

    正确答案:A

  • 第10题：

    一个长方形和一个正方形的周长相等，它们的面积（）。

    • A、正方形大
    • B、长方形大
    • C、相等
    • D、不能确定

    正确答案:A

  • 第11题：

    单选题
    己知正方形的边长，求正方形的周长和面积，经过一下几个步骤，正确的顺序为（） ①输入正方形的边长 ②计算正方形的周长 ③计算正方形的面积 ④输出周长及面积
    A

    ①②③④

    B

    ②①③④

    C

    ②③①④

    D

    ②③④①


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    一个长方形和一个正方形的周长相等，那么它们的面积相比较，（）的面积大。
    A

    正方形

    B

    长方形

    C

    同样大


    正确答案： C
    解析： 暂无解析

  • 第13题：

    给长方形的长增加2，宽增加5恰好可以得到一个面积为100的正方形，则原长方形的周长( )。

    A．13

    B．26

    C．40

    B D．46


    正确答案：B

  • 第14题：

    把一个正方形的一边减少20%，另一边增加2米。得到一个长方形，它与原正方形的面积相等，那么，正方形面积是多少平方米？（ ）

    A．8

    B．10

    C．16

    D．64


    正确答案：D
    设正方形的边长为a，则正方形的面积为a2=(a+2)·a·(1-20%),解方程得a=8，则正方形的面积为64，所以D项为正确答案。

  • 第15题：

    把一个正方形的一边减少20%，另一边增加2米。得到一个长方形，它与原正方形的面积相等，那么，正方形面积是多少平方米?( )

    A. 8
    B. 10
    C. 16
    D. 64

    答案：D
    解析：
    设正方形的边长为a，则正方形的面积为a2=(a+2)*a*(1-20%),解方程得a=8，则正方形的面积为64。故答案为D。

  • 第16题：

    如图，将正方形边长三等分后可得9个边长相等的小正方形，把中间的小正方形去掉，对剩下的8个小正方形，均按上面方法操作。问：对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少？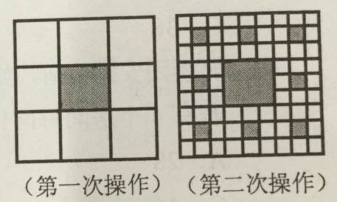

    A.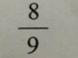
    B.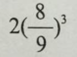
    C.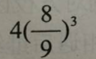
    D.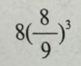

    答案：C
    解析：

  • 第17题：

    给长方形的长增加2，宽增加5恰好可以得到一个面积为100的正方形，则原长方形的周长( )。

    A. 13
    B. 26
    C. 40
    D. 46

    答案：B
    解析：
    故答案为B。

  • 第18题：

    如图，由四个全等的小长方形拼成一个大正方形，每个长方形的面积都是1，且长与宽之比大于等于2，则这个大正方形的面积至少为 ()。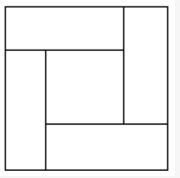

    A.3
    B.4.5
    C.5
    D.5.5

    答案：B
    解析：
    第一步，本题考查几何问题，属于其他几何类。
    第二步，大正方形的面积＝小长方形面积×4＋中间小正方形的面积，由于每个长方形的面积都确定为1，那么要使大正方形的面积最小，则应使中间小正方形的面积最小。
    第三步，设长方形的长为x，宽为y，则中间小正方形的边长为x－y，面积为（x－y）2，由条件可知x≥2y，那么当x＝2y时，中间小正方形的面积（x－y）2最小，大正方形的面积也为最小。已知每个长方形的面积都为1，那么

    第四步，大正方形的面积＝

    因此，选择B选项。

  • 第19题：

    当采光口面积相同，窗底标高一致时，以下几种形状的窗口的采光量大小排序何者为正确?

    • A、正方形>竖长方形>横长方形
    • B、正方形<竖长方形<横长方形
    • C、正方形-竖长方形-横长方形
    • D、横长方形<正方形<竖长方形

    正确答案:A

  • 第20题：

    图形面积相等的圆、正方形，给人的感觉正方形大而圆面积小。


    正确答案:正确

  • 第21题：

    一个长方形和一个正方形的周长相等，那么它们的面积相比较，（）的面积大。

    • A、正方形
    • B、长方形
    • C、同样大

    正确答案:A

  • 第22题：

    己知正方形的边长，求正方形的周长和面积，经过一下几个步骤，正确的顺序为（） ①输入正方形的边长 ②计算正方形的周长 ③计算正方形的面积 ④输出周长及面积

    • A、①②③④
    • B、②①③④
    • C、②③①④
    • D、②③④①

    正确答案:A

  • 第23题：

    单选题
    一个长方形和一个正方形的周长相等，它们的面积（）。
    A

    正方形大

    B

    长方形大

    C

    相等

    D

    不能确定


    正确答案： D
    解析： 暂无解析

相关内容