在平面直角坐标系中,点A(m,6)与点B(2.5,n)关于原点对称,则A、B两点之间的距离为( )。A.5B.12C.13D.8.5
题目
在平面直角坐标系中,点A(m,6)与点B(2.5,n)关于原点对称,则A、B两点之间的距离为( )。
A.5
B.12
C.13
D.8.5
相似考题
更多“在平面直角坐标系中,点A(m,6)与点B(2.5,n)关于原点对称,则A、B两点之间的距离为( )。A.5 ”相关问题
-
第1题:
在平面直角坐标系中,点A(m,6)与点B(2.5,n)关于原点对称,则A、B两点之间的距离为()。A.5
B.12
C.13
D.8.5答案:C解析:因为点A与点B关于原点对称,所以m=2.5,n=-6。两点的坐标分别为A=(-2.5,6)、B
(2.5,-6),则 4、B 两点之间的距离就等于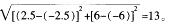
-
第2题:
1、平面直角坐标系下两点A(x1,x2)、B(y1,y2),它们之间的欧氏距离为:sqrt((x1-y1)*(x1-y1)+(x2-y2)*(x2-y2))。扩展到N维空间,每个点的坐标有N维,例如点A(x1,x2,......,xN),类似地也可以计算两点之间的欧氏距离。编程计算N位向量的欧氏距离。
因为Ⅱ 1 :ax+by-z+c=0,Ⅱ 2(xOy) :z=0,而它们的法向量分别为 n 1 =(a,b,-1), n 2 =(0,0,1) 所以它们的夹角为 -
第3题:
在直角坐标系中,已知A(1,2,-4),则点A关于y轴的对称点为______________。
∵ AB =(5,-2,2) ,∴ | AB | = 5 2 +(-2 ) 2 + 2 2 = 33 . 故选B. -
第4题:
用视距测量方法求A、B两点间距离,通过观测得尺间距l=0.386m,竖直角α=6°42',则A、B两点间水平距离为:( )A.38.1m
B.38.3m
C.38.6m
D.37.9m答案:A解析:视距测量是一种不受地形限制,间接地测定出地面两点间距离和高差的光学间接测距方法。利用测量望远镜内十字丝平面上的视距丝及刻有厘米分划的视距标尺,就可以测定测站与目标点之间的水平距离和高差(垂直距离)。按视距测量水平距离计算公式得:D=Klcos2α=100×0.386cos2(6°42')=38.1m;式中,K为视距乘常数。设计时取K=100。 -
第5题:
在直角坐标系xOy中,点M(4,-3)到原点O的距离是()
A.3
B.4
C.5
D.6
(1)由题意,可得 ∵A(-1,1),B(1,1),M(x,y) ∴ MA + MB =(-1-x,1-y)+(1-x,1-y)=(-2x,2-2y) , 由此可得, | MA + MB |= (-2x) 2 + (2-2y) 2 = 4 x 2 +4 y 2 -8y+4 , 又∵ | MA + MB |=4- 1 2 OM ?( OA + OB ) ,且 4- 1 2 OM ?( OA + OB )=4- 1 2 (x,y)?(0,2)=4-y , ∴ 4 x 2 +4 y 2 -8y+4 =4-y , 化简整理得: x 2 3 + y 2 4 =1 ,即为所求曲线C的方程. (2)因为过原点的直线L与椭圆相交的两点M,N关于坐标原点对称, 所以可设P(x,y),M(x 0 ,y 0 ),N(-x 0 ,-y 0 ). ∴P,M,N在椭圆上, ∴ x 2 3 + y 2 4 =1 ,…①. x 20 3 + y 20 4 =1 ,…② ①-②,得 y 2 - y 20 x 2 - x 20 =- 4 3 . 又∵ k PM = y- y 0 x- x 0 , k PN = y+ y 0 x+ x 0 , ∴ k PM ? k PN = y- y 0 x- x 0 ? y+ y 0 x+ x 0 = y 2 - y 20 x 2 - x 20 =- 4 3 , 因此,k PM ?k PN 的值恒等于- 4 3 ,与点P的位置和直线L的位置无关. (3)由于P(x,y)在椭圆C: x 2 3 + y 2 4 =1 上运动,可得x 2 =3- 3 4 y 2 且-2≤y≤2 ∵ MP =(x,y-m), ∴| MP |= x 2 +(y-m ) 2 = 1 4 y 2 -2my+ m 2 +3 = 1 4 (y-4m) 2 -3 m 2 +3 由题意,点P的坐标为(0,2)时, | MP | 取得最小值, 即当y=2时, | MP | 取得最小值,而-2≤y≤2,故有4m≥2,解之得 m≥ 1 2 . 又∵椭圆C与y轴交于D、E两点的坐标为(0,2)、(0,-2),而点M在线段DE上,即-2≤m≤2, ∴ 1 2 ≤m≤2 ,实数m的取值范围是 [ 1 2 ,2] .
