itgle.com

二、数学运算。通过运算，选择最合适的一项。请开始答题：26·从l，2，3，4，?，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为( )。A·134 ‘B．267C．316D．133

题目

二、数学运算。通过运算，选择最合适的一项。请开始答题：

26·从l，2，3，4，?，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为( )。

A·134 ‘

B．267

C．316

D．133

相似考题

1.一、数字推理。给你一个数列.但其中缺少一项，要求仔细观察数列的排列规律，然后从四个供选择的选项中选择你认为最合适最合理的一项来填补空缺项，使之符合原数列的排列规律。请开始答题( 26~ 35 题) :26. 0, 3, 9, 21, ( ), 93A.40B.45C.36D.38

2.从1，2，3，……，50这五十个数中，取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取多少个数( )。A. 21 B. 22C. 23 D. 29

3.二、数学运算。通过运算。选择最合适的一项。请开始答题：26.有两个自然数，它们的和等于297，它们的最大公约数与最小公倍数之和等于693。这Nd"-自然数的差等于多少?( )A.33B．27C．11D．9

4.从1，2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为（ ）。A．134B．267C．316D．133

更多“二、数学运算。通过运算，选择最合适的一项。请开始答题：26·从l，2，3，4，?，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为( )。A·134 ‘B．267C．316D．133”相关问题

  • 第1题：

    二、数学运算。通过运算，选择你认为最合适的一个答案。

    11．x-y=1，x3-3xy-y3=（ ）

    A．1

    B．2

    C．3

    D．5


    正确答案：A
    11．【解析】A。x3-3xy-y3=x3-y3-3xy=（x-y）（x2+xy+y2）-3xy=x2-2xy+y2=（x-y）2=1

  • 第2题：

    二、数学运算。通过运算，选择最合适的一项。

    第10题：1×2×3×4×5×…×3000的积的尾数有几个0？（ ）

    A. 600 B. 700 C. 748 D. 680


    正确答案：C

  • 第3题：

    二、数学运算。通过运算，选择你认为最合适的一个答案。

    第46题：

    （7.2×69×1/2）÷(1.8×2.3×20)=( )

    A.6 B. 3/2 C.6 D. 3/4


    正确答案：C

  • 第4题：

    二、数学运算。通过运算，选择你认为最合适的一个答案。

    第46题：

    对任意实数a、b、c定义运算a*b*c=ab-bc+ca，若1*x*2=2，则x=（ ）

    A．2 B．-2 C．0 D．±1


    正确答案：D

    因为a×b×c＝ab-bc-ca，所以1×x×2=1x-x2+21=2，解得，x=±1 。

  • 第5题：

    从1，2，3，……，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除。问最多可取几个数？（）

    A.14个
    B.15个
    C.16个
    D.17个

    答案：C
    解析：
    任意两个数之积不能被4整除，即两个数分别不能被4整除,那么所取数中最多只能有一个偶数，且该偶数不能为4的倍数;共有15个奇数，所以最多可以取15+1=16个数。故正确答案为C。

  • 第6题：

    从1、2、3、…、n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为多少？( )

    A.106
    B.107
    C.108
    D.109

    答案：C
    解析：
    根据两数之差不能为13，构造(1、14、27、40、…)、(2、15、28、41、…)、(3、16、29、42…)、…、(13、26、39、…)。显然每个括号中均不能取连续的两个数，现要求任取57个数必有两数差为13时，n的最大值，那考虑取57个可能没有两数之差为13时，凡的最小值，显然每组数中取第1、3、5、7、…个数可使n最小，相当于每26个数取前13个数，那么要取57个数，57÷13-4……5，n最小为26×4+5=109.即n为109时就能满足取57个数且可能没有两数之差为13的情况，当n为108时，必然有两个数之差为13，所以n的最大值为108，

  • 第7题：

    三个数的和为252,这三个数分别能被6,7,8整除,而且商相同,则最大的数与最小的数相差

    A.18
    B.20
    C.22
    D.24
    E.26

    答案：D
    解析：
    设商为k,则这三个数为6k,7k,8k,由三个数的和为252,可得6k+7k+8k=252,解得k=12.故8k一6k=2k=24

  • 第8题：

    数学运算。通过运算，选择最合适的一项。
    一列火车途经两个隧道和一座桥梁，第一个隧道长600米，火车通过用时18秒；第二个隧道长480米，火车通过用时15秒；桥梁长800米，火车通过时速度为原来的一半，则火车通过桥梁所需的时间为（ ）

    A．20秒 B．25秒 C．40秒 D．46秒

    答案：D
    解析：
    设火车车长为 米，原来的速度为 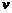米/秒，根据题意可列方程组 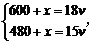解得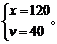 火车过桥时速度为原来的一半，即为20米/秒，则火车通过桥梁所需的时间为（800+120）÷20=46（秒）。

  • 第9题：

    数学运算。通过运算，选择最合适的一项。
    设a、b均为正整数，若11a+7b=132，则a的值为（ ）

    A．6 B．4 C．3 D．5

    答案：D
    解析：
    不定方程求解，可分析未知数所应满足的倍数特征。132为11的倍数，11a是11的倍数，则7b也是11的倍数，则b是11的倍数，令b=11，可得a=5。

  • 第10题：

    对于第n能层，若它作为原子的最外层，则容纳的电子数最多与n-1层相同，当它作为次外层，则其容纳的电子数比n+1层上电子最多能多10个，则第n层为（）

    • A、L能层
    • B、M能层
    • C、N能层
    • D、任意层

    正确答案:B

  • 第11题：

    填空题
    在1和2015之间（包括1和2015在内）不能被4、5、6三个数任意一个数整除的数有（）个。

    正确答案： 1075
    解析： 暂无解析

  • 第12题：

    单选题
    从1，2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为（　　）。
    A

    134

    B

    267

    C

    316

    D

    133


    正确答案： D
    解析：
    取出的N个不同的数，任意三个的和都能被15整除，分三种情况：①这N个数都能被15整除，在1～2007中，能被15整除的数为15×1，15×2，…，15×133，共133个；②这N个数除以15的余数都为，在1～2007中，能被15除余5的数为15×0＋5，15×1＋5，…，15×133＋5，共有134个；②这N个数除以15的余数都为10，在1～2007中，能被15除余10的数的个数为15×0＋10，15×1＋10，…，15×133＋10，共有134个。则N最大为134。

  • 第13题：

    二、数学运算(你可以在题本上运算，遇到难题，你可以跳过不做，待你有时间再返回来做，本部分包括15题。) 请开始答题：

    11.两个数的差是2345，两数相除的商是8，求这两个数之和。( )

    A.2353

    B.2896

    C.3015

    D.3456


    正确答案：C
    11．【答案】C　 根据题意，两数相除商是8，则说明被除数是除数的8倍，两数相减结果2345应为除数的7倍，从而求得除数2345÷7=335，被除数为335×8=2680，两数和为2680＋335=3015，答案为C。

  • 第14题：

    二、数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字．要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    请开始答题：

    91．一个正方体木块放在桌子上，每一面都有一个数，位于对面两个数的和都等于13，小张能看到顶面和两个侧面，看到的三个数和为l8；小李能看到顶面和另外两个侧面，看到的三个数的和为24，那么贴着桌子的这一面的数是多少?( )

    A．4

    B．5

    C．6

    D．7


    正确答案：B
    91．B[解析]项面的数字为(18+24—13—13)÷2=8，所以底面为5。

  • 第15题：

    请教:河北省2012年公务员《行测》标准预测试卷(6)第2大题第7小题如何解答?

    【题目描述】

    第 42 题 从1，2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为（　　）。

    A．134

    B．267

    C．316

    D．133

     


    正确答案：A
    答案分析：

    取出的N个不同的数，任意三个的和都能被15整除，分两种情况：

    (1)这N个数都能被15整除

    在1—2007中，能被15整除的数为15×1，15×2，…，15×133，共有133个。

    (2)这N个数除以15的余数都为5

    在1—2007中，能被15除余5的数为15×0＋5，15×1＋5，…，15×133＋5，共有134个。故N最大为134。

  • 第16题：

    从1.2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为()。

    A．134

    B．267

    C．316

    D．133


    正确答案：A

  • 第17题：

    从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？

    A. 10%
    B. 30%
    C. 60%
    D. 90%

    答案：D
    解析：
    三个数中只要含有1就能满足，共C4,2=6种，三个数中含有2的话，三个数的和必须是偶数，共C3,2-1=2种，不含1和2只有3、4、5能被3整除，因此共有9种满足的情况，总数为c5,3=10，概率为9/10=90%。

  • 第18题：

    从1到100的整数中任取一个数，则该数能被5或7整除的概率为（ ）

    A.0.02
    B.0.14
    C.0.2
    D.0.32
    E.0.34

    答案：D
    解析：

  • 第19题：

    数学运算。通过运算，选择最合适的一项。
    某年的3月有5个星期一和4个星期二，则该年的国庆节是（ ）

    A．星期二 B．星期三 C．星期四 D．星期五

    答案：B
    解析：
    星期日期问题。因为该年的3月有5个星期一和4个星期二，那么3月31日必定是星期一，从4月1日到9月30日共有183天，183÷7=26…1，则9月30日是星期二，所以该年的国庆节是星期三。B项正确。

  • 第20题：

    数学运算。通过运算，选择最合适的一项。
    某商品今年的成本比去年减少15%，由于售价不变，利润率比去年增加了24个百分点，则该商品去年的利润率为（ ）

    A．24% B．30% C．36% D．42%

    答案：C
    解析：
    设该商品去年的利润率为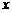 。进行赋值，设该商品去年的成本为100，则今年的成本为85，根据“售价不变”可列方程100×（l+ 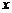）=85×（1+ 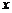+24%），解得 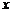=36%。

  • 第21题：

    在1和2015之间（包括1和2015在内）不能被4、5、6三个数任意一个数整除的数有（）个。


    正确答案:1075

  • 第22题：

    从1，2，3，…，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除，问最多可取几个数（）

    • A、14个
    • B、15个
    • C、16个
    • D、17个

    正确答案:C

  • 第23题：

    单选题
    一个四位数“□□□□”分别能被15、12和10整除，且被这三个数整除时所得的三个商的和为1365，问四位数“□□□□”中四个数字的和是多少？（　　）
    A

    17

    B

    16

    C

    15

    D

    14


    正确答案： C
    解析：
    设此数为x，由题意可知，x÷15＋x÷12＋x÷10＝1365，得x＝5460，则四个数字的和是5＋4＋6＋0＝15。

相关内容