itgle.com

如右图，正四面体P-ABC的棱长为口，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：A.1：8B.1：16C.1：32D.1：64

题目

如右图，正四面体P-ABC的棱长为口，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：

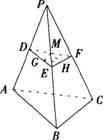
A.1：8

B.1：16

C.1：32

D.1：64

相似考题

1.在平面上，若两个正三角形的边长的比为1：2，则它们的面积比为1：4，类似地，在空间，若两个正四面体的棱长的比为1：2，则它们的体积比为___________ .

2.属于不规则单元的有( )。A、正四面体单元B、正三棱体单元C、任意曲边单元D、任意六面体单元

3.不属于规则单元的是( ) 。A.正四面体单元B.正三棱体单元C.正六面体单元D.曲边单元

4.下列属于不规则单元的有()。A.正四面体单元B.正三棱体单元C.任意四面体单元D.正六面体单元

参考答案和解析
正确答案：D
比为边长比的平方1：16。正四面体P－ABC的表面积是三角形ABC面积的4倍，故所求比例为1：(16×4)＝1：64。
更多“ 如右图，正四面体P-ABC的棱长为口，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：A.1：8B.1：16C.1：32D”相关问题

  • 第1题：

    正四面体的棱长增长10％，则表面积增加（ ）

    A．21％

    B．15％

    C．44％

    D．40％


    正确答案：A

  • 第2题：

    如图，正四面体P-ABC的棱长为a，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：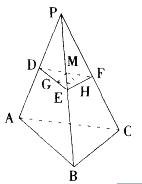


    A.1：8
    B.1：16
    C.1：32
    D.1：64

    答案：D
    解析：
    DE=AB/2=a/2，同理三角形GHM的边长为DE/2=a/4。所以三角形GHM和三角形ABC的面积比为边长比的平方1：16。正四面体P-ABC的表面积是三角形ABC面积的4倍，故所求比例为1：16x4=1：64。

  • 第3题：

    连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体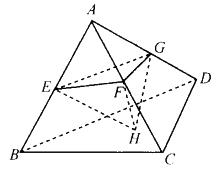

    （如右图所示）。问该多面体与正四面体的体积比是多少？（ ）

    A. 1 : 8
    B. 1 : 6
    C. 1：4
    D. 1 : 2

    答案：C
    解析：
    如图所示，AEFG与ABCD的边长比为1：2，所以二者的面积比为1 : 4。又因为正四面体A—EFG与正四面体A—BCD高的比为1 : 2，所以，正四面体A—EFG与正四面体A—BCD的体积比为1 : 8，所以该多面体与正四面体A—BCD的体积比为2 : 8，即1 : 4。故本题答案为C。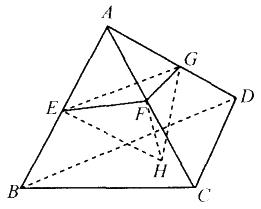

  • 第4题：

    如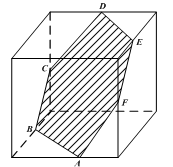，六边形ABCDEF是平面与棱长为2的正方体所截得到的，若A，B，D，E分别是相应的棱的中点，则六边形ABCDEF的面积为



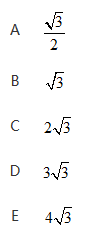    答案：D
    解析：

  • 第5题：

    如图，已知四棱锥P-ABCD底面ABCD为矩形，侧棱PA⊥ABCD，AB=AP=21/2AD=2，E，F分别为PC，AB的中点。
    (I)证明：EF∥面PAD。
    (II)求三棱锥B-PFC的体积。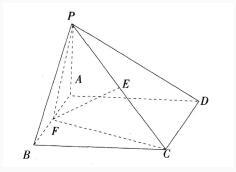


    答案：
    解析：

  • 第6题：

    正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为30°。


    正确答案:正确

  • 第7题：

    填空题
    在四面体P-ABC中共有____对异面直线．

    正确答案： 三对
    解析：
    三对异面直线为PA与BC、PB与AC、PC与AB．

  • 第8题：

    如图，正四面体P-ABC的棱长为a，D、E、F分别为PA、PB、PC的中点，G、H、M 分别为DE，EF，FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为（ ）。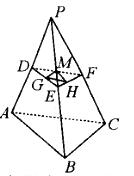


    A. 1 : 8
    B. 1 : 16
    C. 1 : 32
    D. 1 : 64

    答案：D
    解析：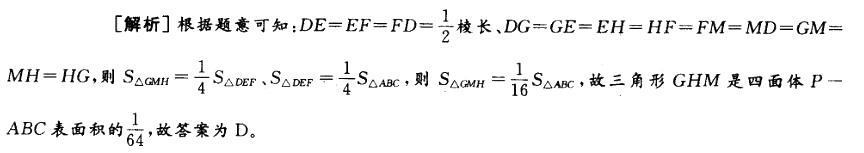

  • 第9题：

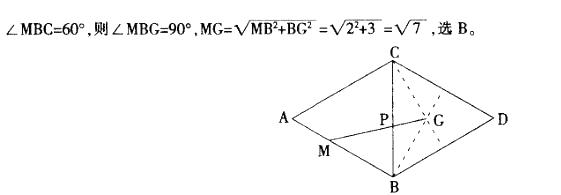
    如图，A-BCD是棱长为3的正四面体，M是棱AB上的一点，且MB=2MA，G是三角形


    答案：B
    解析：
    将面ABC和面BCD展开至一个平面，如图所示，连接BG、CG。要使MP+PG最小，则P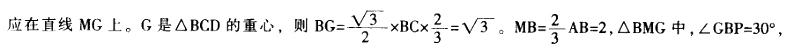

  • 第10题：

    如，正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点，则AF的长为


    答案：A
    解析：

  • 第11题：

    棱长为3的正四面体，以其3个侧面的重心为顶点的三角形面积为：


    答案：A
    解析：
    正四面伴的侧面是等边三角形，其重心为各边中线的交点。如左图可知，重心O将中线

  • 第12题：

    如图，点P为⊙O上一动点，PA，PB为⊙O的两条弦，BE，AF分别垂直于PA，PB，垂足分别为E，F，若∠P=60°，⊙O的半径为4，则EF的长( )。




    答案：C
    解析：
    BE，AF的交点记为G，G即是△ABC垂心，则G点关于AP，BP两条边的对称点M，N都在△ABC外接圆⊙O上。(三角形的垂心关于三边的对称点都在三角形的外接圆上。)则EF是△GMN平行于 MN边的中位线，则EF∥MN,所以∠FEB=∠M=∠FAB。 又因为G为垂心，所以∠PEF+∠FEB=∠FAB+∠PBA=90°，所以∠PEF=∠PBA。所以△PEF∽△PBA，于是


  • 第13题：

    单选题
    相同表面积的四面体、六面体、正十二面体及正二十面体中体积最大的是（　　）
    A

    四面体

    B

    六面体

    C

    正十二面体

    D

    正二十面体


    正确答案： C
    解析：
    相同表面积的空间几何图形，越接近于球，其体积越大。正二十面体是四个图形中最接近于球的立体几何图形，体积最大。

相关内容