itgle.com

在k元回归中，n为样本容量，SSE为残差平方和，SSR为回归平方和，则对回归方程线性关系的显著性进行检验时构造的F统计量为（）。

题目
在k元回归中，n为样本容量，SSE为残差平方和，SSR为回归平方和，则对回归方程线性关系的显著性进行检验时构造的F统计量为（）。


相似考题

1.在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255.4，残差平方和为275，在α=0.05下，F分布的临界值为5.32，则有结论( )。A．F=4.32B．F=7.43C．回归方程不显著D．回归方程显著E．回归方程显著性无法判断

2.收集了n组数据(xi，yi)，i=1，2，…，n，在一元线性回归中用SR表示回归平方和，SE表示残差平方和，由此求得F比，则当( )时在显著性水平α上认为所得到的回归方程是有意义的。A．F＞F1-α(1，n)B．F＞F1-α(1，n-1)C．F＞F1-α(1，n-2)D．F＜F1-α(1，n-2)

3.对方程作显著性检验时，下列叙述（ ）是正确的。A.残差平方和的自由度为25B.残差平方和的自由度为24C.检验统计量F的值为24.986D.检验统计量，的值为43.074

4.对方程作显著性检验时，下列叙述正确的是( )。A．残差平方和的自由度为25B．残差平方和的自由度为24C．检验统计量F的值为24.986D．检验统计量F的值为43.074

更多“在k元回归中，n为样本容量，SSE为残差平方和，SSR为回归平方和，则对回归方程线性关系的显著性进行检验时构造的F统计量为（）。 ”相关问题

  • 第1题：

    已知含有截距项的三元线性回归模型估计的残差平方和为

    已知含有截距项的三元线性回归模型估计的残差平方和为，估计用样本容量为24，则随机误差项的方差估计量为（）。


    参考答案：B

  • 第2题：

    多元回归模型中的解释变量个数为k，那么回归方程显著性检验的F统计量的第一自由度为n—k一1，第二自由度为k。（ ）


    正确答案：B
    多元回归模型中的解释变量个数为k，那么回归方程显著性检验的F统计量的第一自由度为k，第二自由度为n一k一1。

  • 第3题：

    在一元线性回归中，给出n对数据(xi，yi)，i=1，2，…，n，若其回归方程为bx，则下述结论成立的有( )。

    A．总离差平方和ST=Lyy

    B．回归平方和SR=bLxy

    C．残差平方和SE=ST-SR)

    D．残差平方和的自由度为n-1

    E．残差平方和Se=ST-Sf


    正确答案：ABC
    解析：残差平方和的自由度为fE=n-2。

  • 第4题：

    在一元线性回归中，给出n对数据(xi，yi)，i=1，2…，n，若其回归方程为，则下述结论成立的有( )。

    A．总偏差平方和ST＝Lyy

    B．归平方和SR＝bLxy

    C．残差平方和Se＝ST-SR

    D．残差平方和的自由度为n-1

    E．残差平方和Se＝ST-Sf


    正确答案：ABC

  • 第5题：

    在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255. 4，残差平方和为275，在α= 0. 05下，F分布的临界值为5.32，则有结论（ ）。
    A. F=4. 32 B. F=7. 43
    C.回归方程不显著 D.回归方程显著
    E.回归方程显著性无法判断


    答案：B,D
    解析：

  • 第6题：

    设k为回归模型中的解释变量的个数，n为样本容量，RSS为残差平方和，ESS为回归平方和。则对其总体回归模型进行方程显著性检验时构造的F统计量为（ ）。



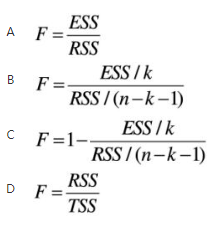    答案：B
    解析：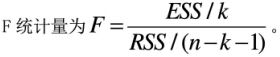

  • 第7题：

    对多元线性回归方程（有k个参数）的显著性检验，所用的F统计量可表示为（ ）



    答案：D,E
    解析：

  • 第8题：

    下列关于t检验与F检验说法正确的有( )。

    A: 对回归方程线性关系的检验是F检验
    B: 对回归方程线性关系的检验是t检验
    C: 对回归方程系数显著性进行的检验是F检验
    D: 对回归方程系数显著性进行的检验是t检验

    答案：A,D
    解析：
    回归方程的显著性检验方法有：①对回归方程线性关系的检验，采用F检验；②
    对回归方程系数显著性进行的检验，采用t检验。线性关系的检验主要是检验因变量同多个自变量的线性关系是否显著，回归系数检验则是对每一个回归系数分别进行单独的检验，它主要用于检验每个自变量对冈变量的影响是否都显著。

  • 第9题：

    总变差平方和SST、回归平方和SSR、回归残差平方和SSE之间的关系是（）。

    • A、SST=SSR+SSE 
    • B、SST=SSR-SSE 
    • C、SSR=SST+SSE 
    • D、SSE=SST+SSR

    正确答案:A

  • 第10题：

    总变动平方和（SST）、回归平方和（SSR）、回归残差平方和（SSE）三者之间的关系可表示为SST=（）。


    正确答案:SSR+SSE

  • 第11题：

    填空题
    总变动平方和（SST）、回归平方和（SSR）、回归残差平方和（SSE）三者之间的关系可表示为SST=（）。

    正确答案： SSR+SSE
    解析： 暂无解析

  • 第12题：

    单选题
    收集了n组数据（xi，yi），i=1，2，…，n，在一元线性回归中用SR表示回归平方和，SE表示残差平方和，由此求得F比，则当（　　）时在显著性水平α上认为所得到的回归方程是有意义的。
    A

    F＞F1-α（1，n）

    B

    F＞F1-α（1，n-1）

    C

    F＞F1-α（1，n-2）

    D

    F＜F1-α（1，n-2）


    正确答案： A
    解析：
    由于fR=1，fE=fT－fR=n-1-1=n-2，所以在显著性水平α上，当F＞F1－α（1，n－2）时认为所得到的回归方程是有意义的。

  • 第13题：

    设K为回归模型中的参数个数（包括截距项），n为样本容量，ESS为残差平方和，RSS为回归平方和。则对总体回归模型进行显著性检验时构造的F统计量为（）。

    A.A

    B.B

    C.C

    D.D


    参考答案：A

  • 第14题：

    在一元线性回归中，给出n对数据(xi，yi)，i=1，2，…，n，若其回归方程为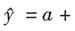bx，则下述结论不成立的有( )。

    A．总偏差平方和ST=Lyy

    B．回归平方和SR=b×Lxy

    C．残差平方和SE=ST-SR

    D．残差平方和的自由度为n-1


    正确答案：D
    解析：总偏差平方和的自由度fr=n-1，回归平方和的自由度fR=1，所以残差平方和的自由度fE=fT-fR=n-2。

  • 第15题：

    对回归方程线性关系的显著性进行检验。其检验过程应包括( )。

    A．提出假设：原假设H0：β1=β2=…=βk=0；备择假设H1：β1，β2：，…，βk不全为零

    B．构造的统计量为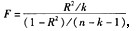：样本统计量服从自由度为(k，n-k-1)的F分布

    C．根据给定的显著性水平，确定临界值Fα(k，n-k-1)

    D．如果F＞Fα(k，n-k-1)，则拒绝原假设

    E．如果F＞Fα(k，n-k-1)，表明在(1-α)的置信概率下，模型的线性关系显著成立，模型通过方程显著性检验


    正确答案：ABCDE

  • 第16题：

    收集了n组数据(xi,yi), i =1， 2，…n，在一元线性回归中用SR表示回归平方和， SE表示残差平方和，由此求得F比，则当（ ）时在显著性水平a上认为所得到的回归方程是有意义的。
    A. F>F1-a(1, n) B. F>F1-a(1, n-1)C. F>F1-a(1, n-2) D. F1-a(1, n-2)


    答案：C
    解析：
    由于fR =1，fE =fT-fR =n-1-1= n -2，所以在显著性水平a上，当F>F1-a(1, n-2) 时认为所得到的回归方程是有意义的。

  • 第17题：

    在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255. 4，残差平方和为275，在a=0.05下，F分布的临界值为5. 32，则有结论（ ）。
    A. F=4. 32 B. F = 7.43
    C.回归方程不显著 D.回归方程显著
    E.回归方程显著性无法判断


    答案：B,D
    解析：
    根据题意，回归平方和SR= 255. 4，残差平方和SE=275, n=10,则总离差平方和的自由度为fT=n-1 =9，回归平方和的自由度fR =1，残差平方和的自由度fE =fT-fR =9-1 =8，所以 ，所以回归方程显著。

  • 第18题：

    设k为回归模型中的参数个数，n为样本容量。则对多元线性回归方程进行显著性检验时，所用的F统计量可表示为（ ）



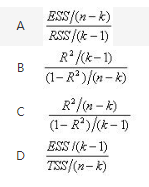    答案：B
    解析：

  • 第19题：

    用 F 检验考查一元线性回归方程的有效性时，总平方和可以被分解为（）

    A.残差平方和、区组平方和
    B.回归平方和、残差平方和
    C.残差平方和、组间平方和、区组平方和
    D.回归平方和、系统误差平方和、残差平方和

    答案：B
    解析：

  • 第20题：

    下列关于t检验与F检验的说法正确的有（ ）。

    A、对回归方程线性关系的检验是F检验
    B、对回归方程线性关系的检验是t检验
    C、对回归方程系数显著性进行的检验是F检验
    D、对回归方程系数显著性进行的检验是t检验

    答案：B,C
    解析：
    回归方程的显著性检验方法有：①对回归方程线性关系的检验，采用F检验；②对回归方程系数显著性进行的检验，采用t检验。线性关系的检验主要是检验因变量同多个自变量的线性关系是否显著，回归系数检验则是对每一个回归系数分别进行单独的检验，它主要用于检验每个自变量对因变量的影响是否都显著。@##

  • 第21题：

    用于检验线性回归方程可信度的统计量F等于（）。

    • A、回归平方和除以残差平方和
    • B、残差平方和除以回归平方和
    • C、平均回归平方和除以平均残差平方和
    • D、平均残差平方和除以平均回归平方和

    正确答案:C

  • 第22题：

    多选题
    在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255.4，残差平方和为275，在α=0.05下，F分布的临界值为5.32，则有结论(　　)。
    A

    F=32    

    B

    F=43

    C

    回归方程不显著    

    D

    回归方程显著

    E

    回归方程显著性无法判断


    正确答案： E,C
    解析： 暂无解析

  • 第23题：

    单选题
    总变差平方和SST、回归平方和SSR、回归残差平方和SSE之间的关系是（）。
    A

    SST=SSR+SSE 

    B

    SST=SSR-SSE 

    C

    SSR=SST+SSE 

    D

    SSE=SST+SSR


    正确答案： A
    解析： 暂无解析

相关内容