已知动点的运动方程为x=t,y=2t2,则其轨迹方程为: A. x=t2-t B. y=2t C. y-2x2=0 D. y+2t2=0
题目
B. y=2t
C. y-2x2=0
D. y+2t2=0
相似考题
参考答案和解析
更多“已知动点的运动方程为x=t,y=2t2,则其轨迹方程为: ”相关问题
-
第1题:
已知微分方程y’+y=f(x),其中f(x)是R上的连续函数.
(Ⅰ)若f(x)=x,求方程的通解.
(Ⅱ)若f(x)是周期为T的函数,证明:方程存在唯一的以T为周期的解.答案:解析:【解】(Ⅰ)若f(x)=x,则方程为y'+y=x通解为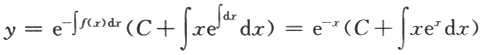
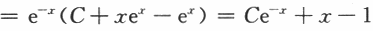
(Ⅱ)设y(x)为方程的任意解,则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T,有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0,有(e^x[y(x+T)-y(x)])'=0,
即e^x[y(x+T)=y(x)]=C.取C=0得y(x+T)-y(x)=0,
y(x)为唯一以T为周期的解. -
第2题:
已知动点的运动方程为x=t,y=2t3。则其轨迹方程为:A. x=t2-t
B. y=2t
C. y-2x2=0
D. y+2x2=0答案:C解析:提示 将t=x代入y的表达式。 -
第3题:
已知曲线y=x2+x-2的切线ι斜率为3,则ι的方程为_________.答案:解析:【答案】3x-y-3=0【考情点拨】本题考查了切线的知识点.
-
第4题:
一平面简谐波沿x轴正向传播,已知x=L(L<λ)处质点的振动方程为y=Acosωt,波速为u,则波动方程为()
- A、y=Acosω[t-(x-L)/u]
- B、y=Acosω[t-(x+L)/u]
- C、y=Acosω[t+(x+L)/u]
- D、y=Acosω[t+(x-L)/u]
正确答案:A -
第5题:
直角坐标表示的动点的运动方程为x=2t,y=2t2,由此可知该动点的轨迹为()。
- A、直线
- B、圆弧
- C、抛物线
- D、椭圆
正确答案:C -
第6题:
已知y倚x的回归方程为:y=ax+b,则可直接导出x倚y的回归方程为:x=(1/a)y-b/a。
正确答案:错误 -
第7题:
已知点的运动方程为①x=5cos5t2,y=5sin5t2;②x=t2,y=2t,由此可得其轨迹方程为①(),②()。
正确答案:x2+y2=25;y2=4x -
第8题:
已知某点沿其轨迹的运动方程为s=b+ct,式中的b、c均为常量,则该点的运动必 是()运动。
正确答案:匀速 -
第9题:
一平面简谐波沿x轴正向传播,已知x=-5m处质点的振动方程为y=Acosπt,波速为u=4m/s,则波动方程为:()
- A、y=Acosπ[t-(x-5)/4]
- B、y=Acosπ[t-(x+5)/4]
- C、y=Acosπ[t+(x+5)/4]
- D、y=Acosπ[t+(x-5)/4]
正确答案:B -
第10题:
单选题(2013)已知动点的运动方程为x=t,y=2t2。则其轨迹方程为:()Ax=t2-t
By=2t
Cy-2x2=0
Dy+2x2=0
正确答案: B解析: 暂无解析 -
第11题:
填空题已知y1=x为微分方程x2y″-2xy′+2y=0之一解,则此方程的通解为____。正确答案: y=c1x+c2x2解析:
设与y2是与y1线性无关的一个特解,则y2′=u+xu′,y2″=2u′+xu″,其代入x2y″-2xy′+2y=0中,得2x2u′+x3u″-2xu-2x2u′+2xu=0,即x3u″=0。u″=0,得u=x,即y2=x2。故原方程的通解为y=c1x+c2x2。 -
第12题:
单选题(2010)已知点的运动方程为x=2t,y=t2-t,则其轨迹方程为:()Ay=t2-t
Bx=2t
Cx2-2x-4y=0
Dx2+2x+4y=0
正确答案: D解析: 暂无解析 -
第13题:
已知点的运动方程为x=2t,y=t2-t则其轨迹方程为:A. y=t2-t
B.x=2t
C. x2-4x-4y=0
D. x2+2x+4y=0答案:C解析:提示 将运动方程中的参数t消去即可。@niutk -
第14题:
已知曲面方程为x-yZ+z2-2x+8y+6z=10,则过点(5,-2.1)的切平面方程为( )。A、2x+3y+2z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0答案:B解析: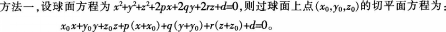
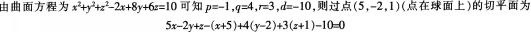

-
第15题:
已知点的运动方程为x=2t3+4,y=3t3-3,则其轨迹方程为()
- A、3x+4y-36=0
- B、3x-2y-18=0
- C、2x-2y-24=0
- D、2x-4y-36=0
正确答案:B -
第16题:
已知直线经过(x1,y1)点,斜率为k(k≠0),则直线方程为y=2kx+2。
正确答案:错误 -
第17题:
已知某点的运动方程为S=a+bt2(S以米计,t以秒计,a、b为常数),则点的轨迹()。
- A、是直线
- B、是曲线
- C、圆周
- D、不能确定
正确答案:D -
第18题:
已知直角坐标描述的点的运动方程为X=f1(t),y=f2(t),z=f3(t),则任一瞬时点的速度、加速度即可确定。
正确答案:正确 -
第19题:
已知点沿其轨迹的运动方程为s=b+ct,式中b、c均为常量,则()
- A、点的轨迹必为直线;
- B、点的轨迹必为曲线;
- C、点必作匀速运动;
- D、点的加速度必为零。
正确答案:C -
第20题:
一平面简谐波沿X轴正向传播,已知x=L(L<λ)处质点的振动方程为y=Acosωt,波速为u,那么x=0处质点的振动方程为()。
- A、y=Acosω(t+L/u)
- B、y=Acosω(t-L/u)
- C、y=Acos(ωt+L/u)
- D、y=Acos(ωt-L/u)
正确答案:A -
第21题:
在平面内运动的点,若已知其速度在x轴及y轴上的分量vx=f1(t),vy=f2(t),问下述说法正确的是()。
- A、点的全加速度a可完全确定
- B、点的运动轨迹可完全确定
- C、点的运动方程可完全确定
- D、点在x轴向的加速度不能确定
正确答案:A -
第22题:
单选题(2005)已知点作直线运动,其运动方程为x=12-t3(x以cm计,t以秒计)。则点在前3秒钟内走过的路程为:()A27cm
B15cm
C12cm
D30cm
正确答案: D解析: 暂无解析 -
第23题:
单选题已知动点的运动方程为x=t,y=2t2,则其轨迹方程为( )。[2013年真题]Ax=t2-t
By=2t
Cy-2x2=0
Dy+2x2=0
正确答案: B解析:
将x=t代入y=2t2,可得轨迹方程为:y-2x2=0。
