已知D为x轴、y轴和抛物线y=1-x2所围成的在第一象限内的闭区域,则
题目
已知D为x轴、y轴和抛物线y=1-x2所围成的在第一象限内的闭区域,则
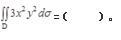
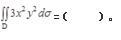
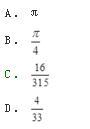
相似考题
参考答案和解析
答案:C
解析:
积分区域D形状如图所示。
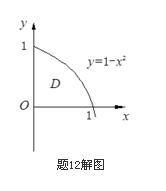
计算得抛物线与x轴、y轴的交点分别为(1,0)、(0,1),从而D={(x,y)|0≤y≤1-x2,x∈[0,1]},则


计算得抛物线与x轴、y轴的交点分别为(1,0)、(0,1),从而D={(x,y)|0≤y≤1-x2,x∈[0,1]},则

更多“已知D为x轴、y轴和抛物线y=1-x2所围成的在第一象限内的闭区域,则 ”相关问题
-
第1题:
在图示xy坐标系下,单元体的最大主应力σ1大致指向( )。
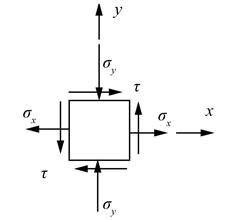 A、 第一象限,靠近x轴
A、 第一象限,靠近x轴
B、 第一象限,靠近y轴
C、 第二象限,靠近x轴
D、 第二象限,靠近y轴答案:A解析:图示单元体的最大主应力σ1的方向可以看作是σx的方向(沿x轴)和纯剪切单元体最大拉应力的主方向(在第一象限沿45°向上)叠加后的合应力的指向,故在第一象限更靠近x轴。 -
第2题:
在图示xy坐标系下,单元体的最大主应力σ1大致指向: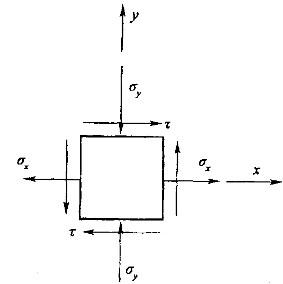
A.第一象限,靠近x轴
B.第一象限,靠近y轴
C.第二象限,靠近x轴
D.第二象限,靠近y轴答案:A解析:提示:图示单元体的最大主应力σ1的方向,可以看作是σx的方向(沿x轴)和纯剪切单元体的最大拉应力的主方向(在第一角限沿45°向上),叠加后的合应力的指向。 -
第3题:
在抛物线y=1-x2与x轴所围成的平面区域内作一内接矩形ABCD,其一边AB在x轴上(如图1-2-4所示).设AB=2x,矩形面积为S(x).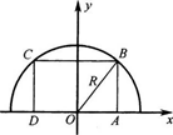
图1—2—3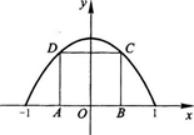
图1—2—4
①写出S(x)的表达式;
②求S(x)的最大值.答案:解析:①S(x)=AB·BC=2xy=2x(1-x2)(0
-
第4题:
曲线y=1-x2与x轴所围成的平面图形的面积S=()·A.2
B.4/3
C.1
D.2/3答案:B解析: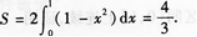
-
第5题:
请计算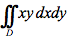 ,其中D是由y=1/x=2,y=x所围成的闭区域答案:解析:
,其中D是由y=1/x=2,y=x所围成的闭区域答案:解析:


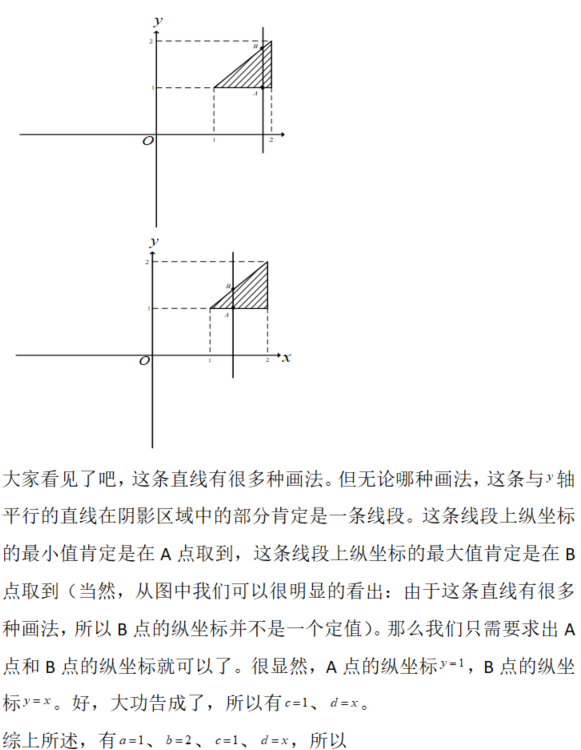



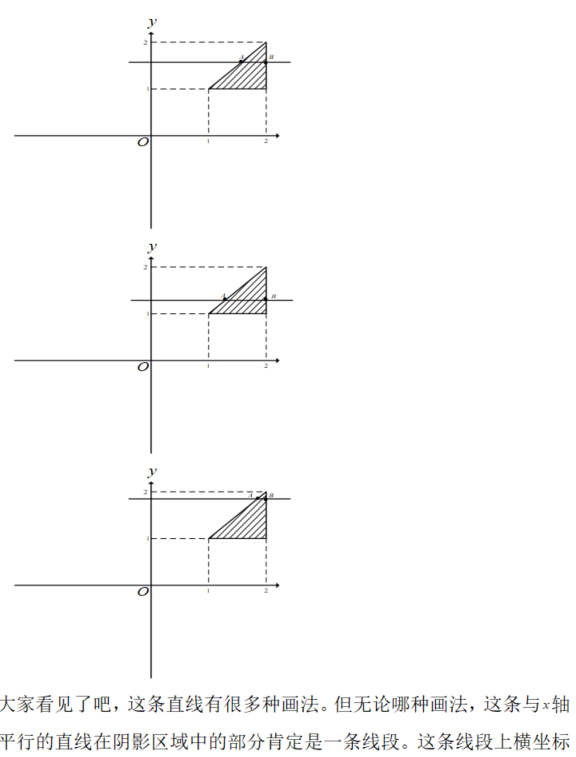


-
第6题:
设D是两个坐标轴和直线x+y=1所围成的三角形区域,则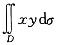 的值为:
的值为:
 答案:C解析:提示:画出积分区域D的图形,把二重积分化为二次积分,
答案:C解析:提示:画出积分区域D的图形,把二重积分化为二次积分,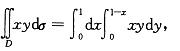 ,计算出最后答案。
,计算出最后答案。 -
第7题:
 该切线与抛物线及x轴成的平面去区域为D,求该区域分别绕x轴和y轴旋转而成的体积。答案:解析:
该切线与抛物线及x轴成的平面去区域为D,求该区域分别绕x轴和y轴旋转而成的体积。答案:解析: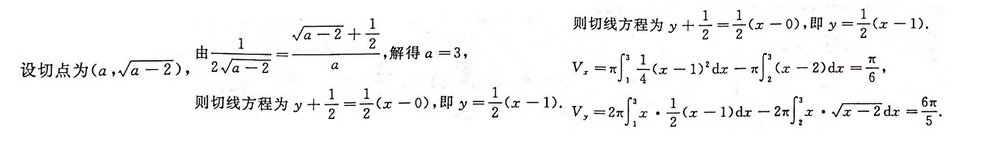
-
第8题:

(1)求f(x)和g(x)围成的平面区域的面积.?
(2)求0≤y≤f(x), 1≤x≤3,绕y轴旋转的体积.?答案:解析:
-
第9题:
设抛物线Y=1-x2与x轴的交点为A、B,在抛物线与x轴所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图2—1所示).设梯形上底CD长为2x,面积为
S(x).
(1)写出S(x)的表达式;
(2)求S(x)的最大值.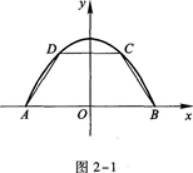 答案:解析:
答案:解析:
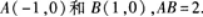
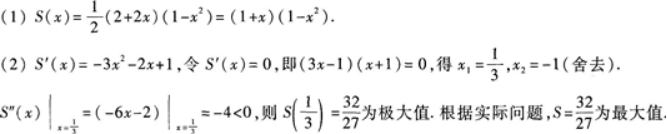
【评析】求函数fx)在[a,b]上的最值时,如果求出fx)的驻点,一定要先判定驻点是否落在[a,b]上. -
第10题:
测量使用的高斯平面直角坐标系与数学使用的笛卡儿坐标系的区别是()。
- A、x与y轴互换,第一象限相同,象限逆时针编号
- B、x与y轴互换,第一象限相同,象限顺时针编号
- C、x与y轴不变,第一象限相同,象限顺时针编号
- D、x与y轴互换,第一象限不同,象限顺时针编号
正确答案:B -
第11题:
已知力F=400N,其与X轴的夹角为30度,则其在X轴和Y轴上的投影是多少()
- A、X=200Y=200
- B、X=200Y=346
- C、X=346Y=200
- D、X=346Y=346
正确答案:C -
第12题:
单选题第一象限内曲线y2+6x=36和坐标轴所围成的图形绕x轴旋转所生成的旋转体的体积为().A36π
B54π
C72π
D108π
正确答案: A解析: 暂无解析 -
第13题:
若D是由x=0,y=0,x2+y2=1所围成在第一象限的区域,则二重积分
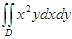
等于( )。
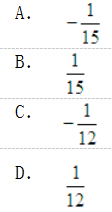 答案:B解析:采用极坐标法求二重积分,具体计算如下:
答案:B解析:采用极坐标法求二重积分,具体计算如下:
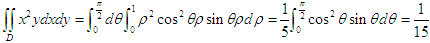
-
第14题:
设抛物线y=1-x2与x轴的交点为A,B,在它们所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图1—2-2所示).设梯形上底CD长为2x,面积为S(x).
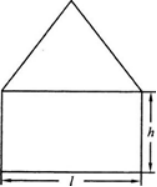
图1一2—1
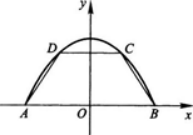
图1—2—2
①写出S(x)的表达式;
②求S(x)的最大值.答案:解析:

-
第15题:
设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·
①求平面图形的面积;
②求平面图形D绕x轴旋转一周所成旋转体的体积Vx.答案:解析: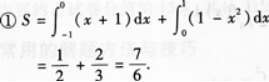
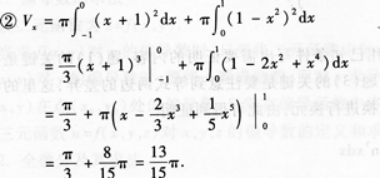
-
第16题:
设f(x,y)为连续函数,且满足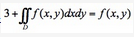 ,其中D是由x轴、y轴、
,其中D是由x轴、y轴、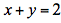 所围成的闭区域答案:解析:
所围成的闭区域答案:解析:

-
第17题:
请计算二重积分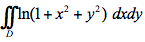 ,其中D是由圆周
,其中D是由圆周 、x轴,y轴所围成的在第一象限内的闭区域答案:解析:
、x轴,y轴所围成的在第一象限内的闭区域答案:解析:



-
第18题:
已知直线在x轴上的截距为-1,在y轴上的截距为1,又抛物线y=x2+bx+c的顶点坐标为(2,-8),求直线和抛物线两个交点横坐标的平方和.答案:解析:
设直线与抛物线两交点的横坐标为x1和x2,则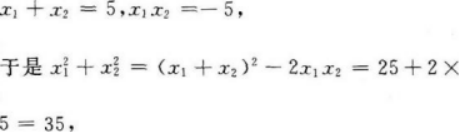
即直线与抛物线两交点的横坐标的平方和为35. -
第19题:
D域由x轴、x2+y2-2x=0(y≥0)及x+y=2 所围成,f(x,y)是连续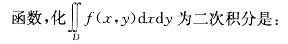
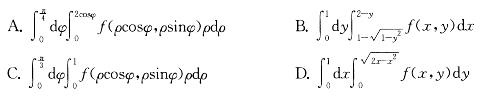 答案:B解析:提示 x2+y2-2x=0,(x-1)2+y2 =1,D由(x-1)2+y2 =1,(y≥0),x+y =2与x
答案:B解析:提示 x2+y2-2x=0,(x-1)2+y2 =1,D由(x-1)2+y2 =1,(y≥0),x+y =2与x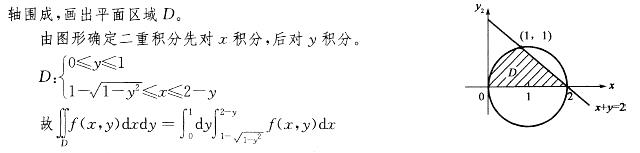
-
第20题:
在图5-49所示xy坐标系下,单元体的最大主应力σ1大致指向( )。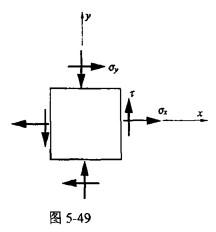
A.第一象限,靠近x轴 B.第一象限,靠近y轴
C.第二象限,靠近x轴 D.第二象限,靠近y轴答案:A解析:提示:σx>σy,τ0 -
第21题:
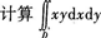 ,其中区域如图5-3所示,由y=x,y=1与Y轴围成.答案:解析:将所给积分化为二次积分.
,其中区域如图5-3所示,由y=x,y=1与Y轴围成.答案:解析:将所给积分化为二次积分.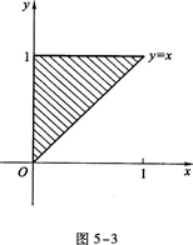
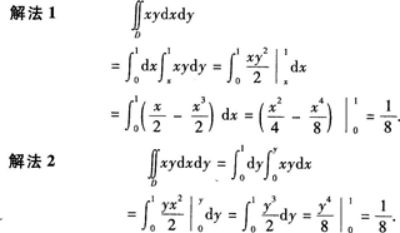
-
第22题:
测量使用的高斯平面直角坐标系与数学使用的笛卡尔坐标系的区别是()。
- A、x与y轴互换,第一象限相同,象限逆时针编号
- B、x与y轴互换,第一象限相同,象限顺时针编号
- C、x与y轴不变,第一象限相同,象限顺时针编号
- D、x与y轴互换,第一象限不同,象限顺时针编号
正确答案:B -
第23题:
单选题A第一象限,靠近x轴
B第一象限,靠近y轴
C第二象限,靠近x轴
D第二象限,靠近y轴
正确答案: D解析:
