某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0. 8 X 10-3 Pa*s,在固壁处y = 0。距壁面y= 7. 5cm处的粘性切应力τ为: A. 2X103Pa B.-32X10-3Pa C.1.48X10-3Pa D.3.3X10-3Pa
题目
某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0. 8 X 10-3 Pa*s,在固壁处y = 0。距壁面y= 7. 5cm处的粘性切应力τ为:
A. 2X103Pa
B.-32X10-3Pa
C.1.48X10-3Pa
D.3.3X10-3Pa
B.-32X10-3Pa
C.1.48X10-3Pa
D.3.3X10-3Pa
相似考题
参考答案和解析
答案:C
解析: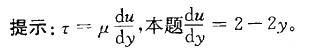
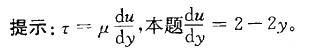
更多“某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0. 8 X 10-3 Pa*s,在固壁处y = 0。距壁面y= 7. 5cm处的粘性切应力τ为: ”相关问题
-
第1题:
一平面简谐波沿X轴正向传播,已知x=L(L<λ)处质点的振动方程为y=Acosωt,波速为u,那么x=0处质点的振动方程为( )。A.y=Acosω(t+L/u)
B.y=Acosω(t-L/u)
C.y=Acos(ωt+L/u)
D.y=Acos(ωt-L/u)答案:A解析:以x=L处为原点,写出波动方程,再令x=-L代入波动方程。 -
第2题:
一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI),则在t=0. 1s时刻,x=2m处质元的振动位移是:
A. 0. 01cm B. 0. 01m
C. -0. 01m D. 0. 01mm答案:C解析: -
第3题:
曲面x^2+cos(xy)+yz+x=0在点(0,1,-1)处的切平面方程为A.Ax-y+z=-2
B.x+y+z=0
C.x-2y+z=-3
D.x-y-z=0答案:A解析: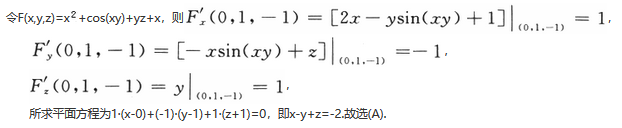
-
第4题:
曲线y=x3-4x+2在点(1,-l)处的切线方程为()A.x-y-2=0
B.x-y=0
C.x+y=0
D.27+y-2=0答案:C解析: -
第5题:
一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI),则在t=0. 1s时刻,x=2m处质元的振动位移是:A. 0. 01cm
B. 0. 01m
C. -0. 01m
D. 0. 01mm答案:C解析: -
第6题:
已知曲面方程为x-yZ+z2-2x+8y+6z=10,则过点(5,-2.1)的切平面方程为( )。A、2x+3y+2z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0答案:B解析: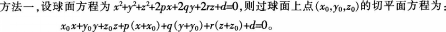
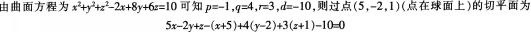

-
第7题:
一平面简谐波沿z轴正向传播,已知x=L(L<λ)处质点的振动方程为Y=Acoswt,波速为u,那么x=0处质点的振动方程为()。
- A、y=Acos(wt+L/u)
- B、y=Acos(wt-L/u)
- C、y=Acosw(t+L/u)
- D、y=Acosow(t-L/u)
正确答案:C -
第8题:
不可压缩流体平面流动在y方向的速度分量为uy=y2-2x+2y,根据连续性方程可知,速度在x方向的分量ux为()。
- A、-(2yx+2x)+f(y)
- B、2x(y+1)
- C、-(2yx+2y)+f(x)
- D、2x(y+1)+c
正确答案:A -
第9题:
已知平面简谐波的波动方程式为y=8cos2π(2t-x/100)(cm),则t=2.1s时,在X=0处相位为(),在x=0.1m处相位为()。
正确答案:8.4π;8.40π -
第10题:
单选题某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0.8×10-3Pa·s,在固壁处y=0。距壁面y=7.5cm处的粘性切应力τ为()A2×103Pa
B-32×10-3Pa
C1.48×10-3Pa
D3.3×10-3Pa
正确答案: A解析: τ=μ(du/dy),本题du/dy=2-2y。 -
第11题:
问答题在平板壁面上的湍流边界层中,流体的速度分布方程可用布拉修斯1/7次方定律表示ux/u0=(y/δ)1/7试证明该式在壁面附近(即y→0处)不能成立。正确答案: 由于该公式中的δ为湍流边界层的厚度,而在壁面附近(即y→0处)边界层的流动为层流,此时δ已不再适用,因此该公式在壁面附近(即y→0处)不能成立。解析: 暂无解析 -
第12题:
单选题函数y=f(x)是由方程xy+2lnx=y4所确定,则曲线y=f(x)在点(1,1)处的切线方程为( )。Ax-y=0
Bx+y=0
C-x-y=0
D-x+y=0
正确答案: C解析:
xy+2lnx=y4两端对x求导,得y+xy′+2/x=4y3·y′。x=1时,y=1,y′(1)=1,则切线方程为y-1=x-1,即x-y=0。 -
第13题:
—平面简谐波沿x轴正方向传播,振幅A=0. 02m,周期T=0. 5s,波长λ=100m,原点处质元的初相位φ=0,则波动方程的表达式为:A.y=0.02cos2π(t/2-0.01x) (SI)
B.y=0.02cos2π(2t-0.01x) (SI)
C.y=0.02cos2π(t/2-100x) (SI)
D.y=0.02cos2π(2t-100x) (SI)答案:B解析:
-
第14题:
某平面流动的流速分布方程为ux=2y-y2,流体的动力粘度为μ=0. 8 X 10-3 Pa?s,在固壁处y = 0。距壁面y= 7. 5cm处的粘性切应力τ为:
A. 2X103Pa
B.-32X10-3Pa
C.1.48X10-3Pa
D.3.3X10-3Pa答案:C解析: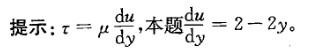
-
第15题:
曲面z=x(1-siny)+y^2(1-sinx)在点(1,0,1)处的切平面方程为________.答案:1、2x-y-z=1.解析:
-
第16题:
曲线y=x3-4x+2在点(1,-1)处的切线方程为( )A.x-y-2-0
B.x-y=0
C.x+y=0
D.x+y-2=0答案:C解析: -
第17题:
曲线y=X2+4在(0,4)处的法线方程为( )。A.y=0
B.y=4
C.x=0
D.x=4答案:C解析:f(x)'=2x,故f'(0)=0,切线斜率为0,法线与切线相互垂直且过点(0,4),故法线方程为x=0。 -
第18题:
已知某水流流速分布为μ=0.72y1/10,u的单位为m/s,y为距壁面的距离,单位为m。 (1)求y=0.1、0.5、1.0m处的流速梯度; (2)若水的运动粘滞系数ν=0.1010cm2/s,计算相应的切应力。

略 -
第19题:
一平面简谐波沿X轴正向传播,已知x=L(L<λ)处质点的振动方程为y=Acos(∞t+φ0),波速为u,那么x=0处质点的振动方程为:()
- A、y=Acos[ω(t+L/u)+φ0]
- B、y=Acos[ω(t-L/u)+φ0]
- C、y=Acos[ωt+L/u+φ0]
- D、y=Acos[ωt-L/u+φ0]
正确答案:A -
第20题:
一平面简谐波沿X轴正向传播,已知x=L(L<λ)处质点的振动方程为y=Acosωt,波速为u,那么x=0处质点的振动方程为()。
- A、y=Acosω(t+L/u)
- B、y=Acosω(t-L/u)
- C、y=Acos(ωt+L/u)
- D、y=Acos(ωt-L/u)
正确答案:A -
第21题:
单选题曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为( )。A3(x-1)+2(y-2)=0
B4(x-1)+2(y-2)=0
C3(x-1)+(y-2)=0
D4(x-1)+(y-2)=0
正确答案: C解析:
构造函数F(x,y,z)=z-ez+2xy-3,则Fx′=2y,Fy′=2x,Fz′=1-ez。故将点(1,2,0)代入上式,即可得此点处切平面的法线向量为n=(4,2,0),则切平面方程为4(x-1)+2(y-2)=0。 -
第22题:
单选题曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为( )。A4(x+1)+2(y-2)=0
B4(x-1)+2(y-2)=0
C4(x-1)-2(y-2)=0
D4(x-1)+2(y+2)=0
正确答案: B解析:
构造函数F(x,y,z)=z-ez+2xy-3,则Fx′=2y,Fy′=2x,Fz′=1-ez。故将点(1,2,0)代入上式,即可得此点处切平面的法线向量为n=(4,2,0),则切平面方程为4(x-1)+2(y-2)=0。 -
第23题:
单选题函数y=f(x)是由方程xy+2lnx=y4所确定,则曲线y=f(x)在点(1,1)处的切线方程为( )。A-x-y=0
Bx-y-1=0
Cx-y=0
Dx+y=0
正确答案: A解析:
xy+2lnx=y4两端对x求导,得y+xy′+2/x=4y3·y′。x=1时,y=1,y′(1)=1,则切线方程为y-1=x-1,即x-y=0。

