itgle.com

设向量α与向量β的夹角θ＝π/3，模|α|＝1，|β|＝2，则模|α＋β|等于（　　）

题目
设向量α与向量β的夹角θ＝π/3，模|α|＝1，|β|＝2，则模|α＋β|等于（　　）


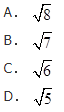
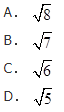
相似考题

1.设向量α=（1，2，-2），β=（2，a，3），且α与β正交，则a=_________.

2.已知平面向量a=（1，1），b=（1，-l），则两向量的夹角为（ ）A.AB.BC.CD.D

3.设向量a=(-2，4，4)，b=(0，6，3)，则a与b的夹角为( ).A. B. C. D.

4.已知向量a,b,c是三个具有公共起点的非零向量,且|a|=2|b|=2,又a·b=-1, 〈a-c,b-c 〉=π/3 ,则当|a-c|=7时,向量a与c的夹角是____.

更多“设向量α与向量β的夹角θ＝π/3，模|α|＝1，|β|＝2，则模|α＋β|等于（　　） ”相关问题

  • 第1题：

    设向量x垂直于向量a=(2，3，-1)和b=(1，-2，3)且与c=(2，-1，1)的数量积为-6，则向量x=( )。

    A.(-3，3，3)
    B.(-3，1，1)
    C.(0，6，0)
    D.(0，3，-3)

    答案：A
    解析：
    由题意可得，x//a×b，而a×b=(2，3，-1)×(1，﹣2，3)=(7，﹣7，﹣7)=7(1，﹣1，﹣1)，所以x=(x，﹣x，﹣x)。再由-6=x·c=(x，-x，-x)·(2，-1，1)=2x得x=-3，所以x=(-3，3，3)。

  • 第2题：

    设a1,a2,3向量组线性无关，则下列向量组线性相关的是（ ）


    答案：A
    解析：

  • 第3题：

    设a，b为非零向量，且满足(a+3b)⊥(7a-5b)，(a-4b)⊥(7a-2b)，则a与b的夹角θ=( )。

    A.0
    B.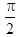
    C.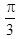
    D.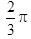

    答案：C
    解析：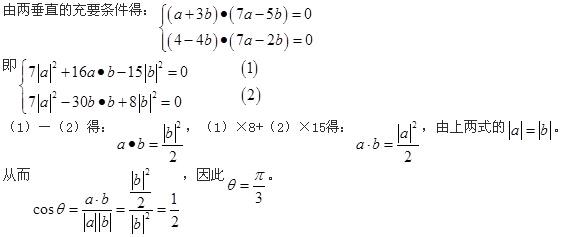

  • 第4题：

    已知｜a｜=1，｜b｜=6，a?(b-a)=2，则向量a与b的夹角是(　　).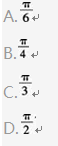


    答案：C
    解析：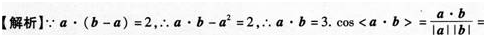

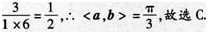
  • 第5题：

    设矩阵，α1，α2，α3为线性无关的3维列向量组，则向量组Aα1，Aα2，Aα3的秩为_________.


    答案：1、2.
    解析：
    因(Aα1，Aα2，Aα3)=A(α1，α2，α3)，又α，α，α是三维线性无关列向量，所以(α1，α2，α3)为三阶可逆矩阵故r(Aα1，Aα2，Aα3)=r(A)=2.

  • 第6题：

    设向量组A：α1=（t，1，1），α2=（1，t，1），α3=（1，1，t）的秩为2，则t等于（）．

    • A、1
    • B、-2
    • C、1或-2
    • D、任意数

    正确答案:B

  • 第7题：

    设列向量p=［1，-1，2］T是3阶方阵相应特征值λ的特征向量，则特征值λ等于（）．

    • A、3
    • B、5
    • C、7
    • D、不能确定

    正确答案:B

  • 第8题：

    单选题
    设向量组A：α1=（t，1，1），α2=（1，t，1），α3=（1，1，t）的秩为2，则t等于（）．
    A

    1

    B

    -2

    C

    1或-2

    D

    任意数


    正确答案： D
    解析： 暂无解析

  • 第9题：

    单选题
    设向量x垂直于向量a=（2，3，-1）和b=（1，-2，3），且与c=（2，-1，1）的数量积为-6，则向量x=（　　）。
    A

    （-3，3，3）

    B

    （-3，1，1）

    C

    （0，6，0）

    D

    （0，3，-3）


    正确答案： B
    解析：
    由题意可得，x∥a×b，而a×b=（2，3，-1）×（1，-2，3）=（7，-7，-7）=7（1，-1，-1），所以x＝k（1，－1，－1）。再由x•c＝2k＋k－k＝2k＝-6，得k＝－3，所以x＝（－3，3，3）。

  • 第10题：

    单选题
    设列向量p=［1，-1，2］T是3阶方阵相应特征值λ的特征向量，则特征值λ等于（）．
    A

    3

    B

    5

    C

    7

    D

    不能确定


    正确答案： C
    解析： 暂无解析

  • 第11题：

    设α,β为四维非零列向量,且α⊥β,令A=αβ^T,则A的线性无关特征向量个数为().

    A.1
    B.2
    C.3
    D.4

    答案：C
    解析：

  • 第12题：

    设向量组A：a1=(1，-1，0)，a2=(2，1，t)，a3=(0，1，1)线性相关，则t等于( ).

    A.1
    B.2
    C.3
    D.0

    答案：C
    解析：

  • 第13题：

    设随机向量（X，Y）的联合分布律为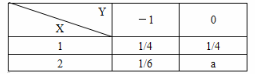

    则a的值等于（　　）。

    A．1/3
    B．2/3
    C．1/4
    D．3/4

    答案：A
    解析：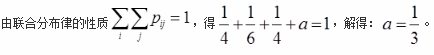

  • 第14题：

    设α1,α2,…,αn为n个线性无关的n维列向量,且与向量β正交.证明：向量β为零向量.


    答案：
    解析：

  • 第15题：

    设向量组I：α1α2αr…，可由向量组Ⅱβ1,β2,…βs：线性表示，下列命题正确的是( )。

    A.若向量组I线性无关．则r≤S
    B.若向量组I线性相关，则r>s
    C.若向量组Ⅱ线性无关，则r≤s
    D.若向量组Ⅱ线性相关，则r>s

    答案：A
    解析：
    由于向量组I能由向量组Ⅱ线性表示，所以r(I)≤r(Ⅱ)，即

  • 第16题：

    设向量组A：α1=（1，-1，0），α2=（2，1，t），α3=（0，1，1）线性相关，则t等于（）。

    • A、1
    • B、2
    • C、3
    • D、0

    正确答案:C

  • 第17题：

    单选题
    设n维列向量组α1，α2，…，αm（m＜n）线性无关，则n维列向量组β1，β2，…，βm线性无关的充分必要条件是（　　）.
    A

    向量组α1，α2，…，αm可以由β1，β2，…，βm线性表示

    B

    向量组β1，β2，…，βm可以由α1，α2，…，αm线性表示

    C

    向量组α1，…，αm与向量组β1，…，βm等价

    D

    矩阵A=（α1，…，αm）与矩阵B=（β1，…，βm）β）m


    正确答案： C
    解析：
    例如α1=（1，0，0，0），α2=（0，1，0，0），β1=（0，0，1，0），β2=（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β1，β2，…，βm线性无关．

  • 第18题：

    单选题
    设n阶方阵A＝（α(→)1，α(→)2，…，α(→)n），B＝（β(→)1，β(→)2，…，β(→)n），AB＝（γ(→)1，γ(→)2，…，γ(→)n），记向量组（Ⅰ）：α(→)1，α(→)2，…，α(→)n；（Ⅱ）： β(→)1，β(→)2，…，β(→)n；（Ⅲ）：γ(→)1，γ(→)2，…，γ(→)n。如果向量组（Ⅲ）线性相关，则（　　）。
    A

    向量组（Ⅰ）与（Ⅱ）都线性相关

    B

    向量组（Ⅰ）线性相关

    C

    向量组（Ⅱ）线性相关

    D

    向量组（Ⅰ）与（Ⅱ）中至少有一个线性相关


    正确答案： D
    解析：
    由向量组（Ⅲ）线性相关，知矩阵AB不可逆，即|AB|＝|A|·|B|＝0，因此|A|、|B|中至少有一个为0，即A与B中至少有一个不可逆，故向量组（Ⅰ）与（Ⅱ）中至少有一个线性相关。

  • 第19题：

    单选题
    设n维列向量组α(→)1，α(→)2，…，α(→)m（m＜n）线性无关，则n维列向量组β(→)1，β(→)2，…，β(→)m线性无关的充分必要条件是（　　）。
    A

    向量组α(→)1，α(→)2，…，α(→)m可以由β(→)1，β(→)2，…，β(→)m线性表示

    B

    向量组β(→)1，β(→)2，…，β(→)m可以由α(→)1，α(→)2，…，α(→)m线性表示

    C

    向量组α(→)1，α(→)2，…，α(→)m与向量组β(→)1，β(→)2，…，β(→)m等价

    D

    矩阵A＝（α(→)1，α(→)2，…，α(→)m）与矩阵B＝（β(→)1，β(→)2，…，β(→)m）等价


    正确答案： D
    解析：
    例如α(→)1＝（1，0，0，0），α(→)2＝（0，1，0，0），β(→)1＝（0，0，1，0），β(→)2＝（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；
    D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β(→)1，β(→)2，…，β(→)m线性无关。

相关内容