itgle.com

在重力大小为W、半径为r的卷筒A上，作用一力偶矩m =aφ的力偶，其中φ为转角，a为常数。卷筒的绳索拉动水平面上的重物B（如图所示）。设重物B的重力大小为WB，它与水平面之间的动滑动摩擦系数为f'，绳的质量不计。当卷筒转过两圈时，作用于系统上的力偶的功W1和摩擦力的功W2分别为：

题目
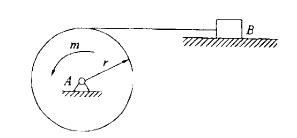
在重力大小为W、半径为r的卷筒A上，作用一力偶矩m =aφ的力偶，其中φ为转角，a为常数。卷筒的绳索拉动水平面上的重物B（如图所示）。设重物B的重力大小为WB，它与水平面之间的动滑动摩擦系数为f'，绳的质量不计。当卷筒转过两圈时，作用于系统上的力偶的功W1和摩擦力的功W2分别为：


相似考题

1.图示三铰支架上作用两个大小相等、转向相反的力偶m1和m2，其大小均为100kN * m，支架重力不计。支座B的反力FB的大小和方向为：

2.已知杆AB和杆CD的自重不计，且在C处光滑接触，若作用在杆AB上力偶矩为M1，若欲使系统保持平衡，作用在CD杆上力偶矩M2的，转向如图所示，则其矩值为：

3.图示两重物的质量均为m，分别系在两软绳上。此两绳又分别绕在半径各为r与2r，并固结在一起的两圆轮上。两圆轮构成的鼓轮的质量亦为m，对轴O的回转半径为ρ0外。两重物中一铅垂悬挂，一置于光滑平面上。当系统在左重物重力作用下运动时，鼓轮的角加速度α为：

4.一绳索跨过匀质滑轮B，绳的一端挂一重物A；另一端缠绕一匀质圆柱C，如图所示。已知重物A的质量为mA；定滑轮B和圆柱C的质量分别为mB和mC，它们的半径均为r。绳的质量略去不计，它对定滑轮无相对滑动。设mB=mC=2mA，则定滑轮与圆柱之间绳索的拉力T为( )。

更多“在重力大小为W、半径为r的卷筒A上，作用一力偶矩m =aφ的力偶，其中φ为转角，a为常数。卷筒的绳索拉动水平面上的重物B（如图所示）。设重物B的重力大小为WB，它与水平面之间的动滑动摩擦系数为f'，绳的质量不计。当卷筒转过两圈时，作用于系统上的力偶的功W1和摩擦力的功W2分别为： ”相关问题

  • 第1题：

    如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计质量的软绳上，绳绕过勻质定滑轮，滑轮半径为r，质量为m，则此滑轮系统对转轴O之动量矩为：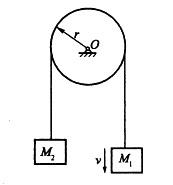



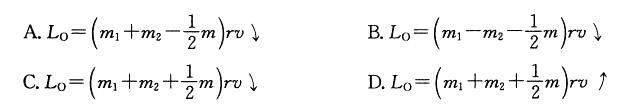    答案：C
    解析：
    根据动量矩定义和公式：Lo=Mo(m1v)+Mo(m2v)+Jo轮ω

  • 第2题：

    匀质圆轮重力为W，其半径为r，轮上绕以细绳，绳的一端固定于A点，如图所示。当圆轮下降时，轮心的加速度ac和绳子的拉力T的大小分别为：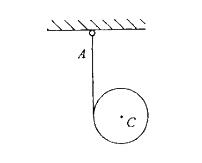



    答案：A
    解析：
    提示：应用平面运动微分方程得:Jcα=Mc(F)；mac=∑F。

  • 第3题：

    已知杆AB和杆CD的自重不计，且在C处光滑接触，若作用在杆AB上的力偶的矩为m1，则欲使系统保持平衡，作用在CD杆上的力偶矩m2，转向如图所示，其矩的大小为：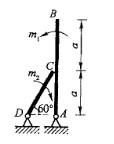



    答案：A
    解析：
    提示:根据受力分析，A、C、D处的约束力均为水平方向，分别考虑杆AB、DC的平衡，采用力偶的平衡方程即可。

  • 第4题：

    三铰拱上作用有大小相等，转向相反的二力偶，其力偶矩大小为M，如图所示。略去自重，则支座A的约束力大小为：


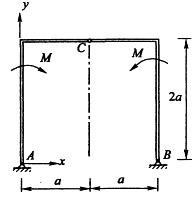    答案：B
    解析：
    根据受力分析，A、B、C处的约束力均为水平方向，分别考虑AC、BC的平衡，釆用力偶的平衡方程即可。

  • 第5题：

    如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统的动量为：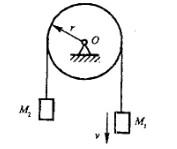



    答案：B
    解析：
    提示:根据动量的定义p=∑mivi。

  • 第6题：

    下列情况中，易造成起重机发生重物失落事故的是（）。

    A.钢丝绳在卷筒上余绳为一圈
    B.有下降限位保护装置
    C.吊装绳夹角＜120°
    D.钢丝绳在卷筒上用压板固定

    答案：A
    解析：
    起重机机械失落事故主要是发生在起升机构取物缠绕系统中，每根钢丝绳在卷筒上的极限安全圈数要在2圈以上，并且有下降限位保护装置。

  • 第7题：

    如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统对转轴O之动量矩为：



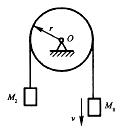    答案：C
    解析：
    提示 根据动量矩定义和公式:LO= MO(m1v) + MO(m2v)+JO轮w。

  • 第8题：

    已知杆AB和杆CD的自重不计，且在C处光滑接触，若作用在杆上的力偶的矩为m1,则欲使系统保持平衡，作用在CD杆上的力偶矩m2，转向如图4-14所示，其矩的大小为（ ）。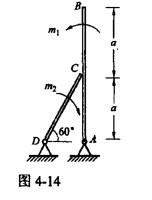



    答案：A
    解析：
    提示：作用在AB杆C处的约束力为水平方向，根据力偶的性质，A、D处约束力应满足二力平衡原理。

  • 第9题：

    力偶的三要素为：力偶矩的大小；力偶的（）；力偶作用面的方位。


    正确答案:转向

  • 第10题：

    图示机构中各杆的自重不计，BC杆水平，α=30°，在C点悬挂重物的重力大小W=1500kN，在B点作用一力P，其大小等于500kN，设它与铅直线的夹角为θ。则当机构平衡时，θ角的大小为( )。


    A.θ=30°或θ=45°
    B.θ=0°或θ=60°
    C.θ=45°或θ=90°
    D.θ=30°或θ=90°

    答案：B
    解析：
    分别研究B点及C点，且分别列垂直于AB及DC轴的投影方程

  • 第11题：

    图示均质圆轮，质量m，半径R，由挂在绳上的重为W的物块使其绕质心轴O转动。设重物的速度为v，不计绳重，则系统动量、动能的大小是（　　）。




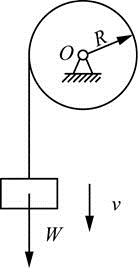
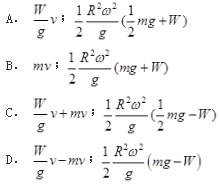    答案：A
    解析：

  • 第12题：

    两重物的质量均为m，分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两轮上。两圆轮构成之鼓轮的质量亦为m，对轴O的回转半径为ρO。两重物中一铅垂悬挂，一置于光滑平面上。当系统在左重物重力作用下运动时，鼓轮的角加速度α为：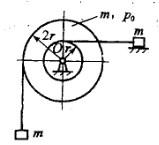



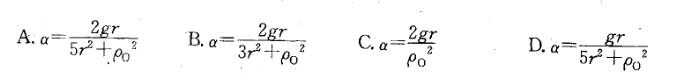    答案：A
    解析：

  • 第13题：

    在两个半径及质量均相同的均质滑轮A及B上，各绕一不计质量的绳，如图所示，轮B绳末端挂一重量为P的重物；轮A绳末端作用一铅垂向下的力P。则此两轮的角加速度大小之间的关系为（　　）。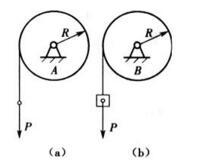


    答案：B
    解析：

  • 第14题：

    起重机械重物失落事故主要发生在起重圈养系统中，如脱绳、脱钩、断绳和断钩。下列状况中，可能造成重物失落事故的是()。

    A.钢丝绳在卷筒上的余绳为1圈
    B.有下降限位保护
    C.吊装绳夹角小于120o
    D.钢丝绳在卷筒上用压板固定

    答案：A
    解析：
    起重机械重物坠落事故主要是发生在起升机构取物缠绕系统中，如脱绳、脱钩、断绳和断钩。每根起升钢丝绳两端的固定也十分重要,如钢丝绳在卷筒上的极限安全圈是否能保证在2圈以上,是否有下降限位保护,钢丝绳在卷筒装置上的压板固定及楔块固定是否安全可靠。另外钢丝绳脱槽(脱离卷筒绳槽)或脱轮(脱离滑轮),也会造成失落事故。

  • 第15题：

    案例：
    学习了“机械和功”相关内容后，某教师为检测学生的掌握情况，进行了相关测试。其中一题某学生的解答如下!
    题目：
    如图7所示，重为20 N的物块A由静止从光滑斜面顶端滑下，最终静止在水平面上。斜面高5 m，长8 m，物块在斜面上滑动时间为5 s，在水平面上滑动距离为12 m。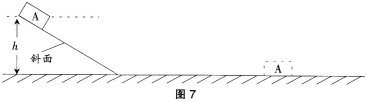

    求：①物块在水平面上滑动过程中，重力对物块做的功：
    ②物块在斜面上滑动过程中，重力对物块做功的功率。
    解：①设重力为G，由已知物块水平距离s为12 m．
    根据功计算公式得：
    重力做功：W=G?s=20 N×12m=240 J
    ②由已知斜面长L为8 m，根据功计算公式得：
    重力做功：W=G?L=20 N×8 m=160 J
    设功率为P，由已知时间t为5 s，根据功率定义公式得：

    答：物块在水平面上滑动重力做功240 J：
    在斜面上滑动重力做功的功率为32 W。
    问题：
    (1)指出这道测试题能检测学生所学的知识点。(4分)
    (2)给出题目的正确解答。(6分)
    (3)针对学生解答过程存在的问题，设计一个教学片段或思路，帮助学生解决此类问题。(10分)


    答案：
    解析：
    (1)功和功率的定义及计算公式。 (2)正确解答：
    ①物块在水平面滑动时，运动方向时刻与重力方向垂直，重力对物块做功恒为零。
    ②物块在斜面滑动过程中，下降的高度h=5 m，
    根据功计算公式得重力做功W=Gh=20 N×5 m=100 J．
    设功率为P，由已知时间t=5 s，根据功率公式得

    (3)教学片段：
    师：同学们．大家从题目中可以知道哪些信息?
    生1：重力的大小、斜面的高度和长度。
    生2：物块下滑的时间和在水平面上滑动的距离。
    师：第一问要求解的是重力做功大小，那大家想一想力做功的条件是什么?
    生：力的方向和物体运动方向不能成90。。
    师：非常好．那大家看一下滑块在下滑过程和水平面上滑动过程中重力与运动方向是否垂直?是否做功?
    生1：下滑时不垂直，有一个角度，说明重力做了功。
    生2：水平面上滑动时重力与运动方向垂直，这表明物块在水平面上滑动时重力不做功。
    师：只要用做功条件去判断，就能知道重力在水平面上滑动时不做功。第二问要求解的是下滑过程中重力对物体做功的功率，那功率是什么，怎样计算?

    师：我们知道时间是5 S，那重力在下滑过程中做功是多少呢?
    生：重力做功等于重力的大小乘以下降高度．所以W=G?h=20 N×5 m=100 J。
    师：那大家把重力做的功代入功率计算公式中计算一下。

    师：好的，大家都明白了吧。
    生：明白。

  • 第16题：

    如图4-63所示，两重物m1和m2的质量分别为m1和m2，两重物系在不计质量的软绳上，绳绕过均质定滑轮，滑轮半径为r,质量为M,则此滑轮系统对转轴O之动量矩为（）。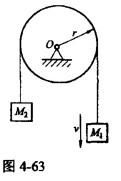



    答案：C
    解析：
    提示：根据动量矩定义和公式

  • 第17题：

    用绞磨吊装重物，设重物重W=2000N，绞杠长500毫米，卷筒半径为125毫米，在不计磨擦力时计算需要用多大的力F，才能绞动重物？


    正确答案: 根据杠杆原理：
    F×500=W×125
    F=（2000×125）/500=500N
    答：需要用500N的力，就可以绞动。

  • 第18题：

    问答题
    用绞磨吊装重物，设重物重W=2000N，绞杠长500毫米，卷筒半径为125毫米，在不计磨擦力时计算需要用多大的力F，才能绞动重物？

    正确答案： 根据杠杆原理：
    F×500=W×125
    F=（2000×125）/500=500N
    答：需要用500N的力，就可以绞动。
    解析： 暂无解析

相关内容