itgle.com

对于函数f（x，y）＝xy，原点（0，0）（　　）。 A．不是驻点 B．是驻点但非极值点 C．是驻点且为极小值点 D．是驻点且为极大值点

题目
对于函数f（x，y）＝xy，原点（0，0）（　　）。

A．不是驻点
B．是驻点但非极值点
C．是驻点且为极小值点
D．是驻点且为极大值点
相似考题

1.在关系模式R á U, F ñ 中，如果X®Y，且存在X的一个真子集X′，有X′®Y ，则称Y对X的依赖为 （ ） 函数依赖。

2.设函数f(x，y)在点(0，0)的某邻域内有定义，且fx(0，0)=3，fy(0，0)=-1，则有( ).A. B.曲面z=f(x，y)在点(0，0，f(0，0))的一个法向量为3i-j+k C. D.

3.下列( )项是在D={(x，y)|x2+y2≤1，x≥0，y≥0)上的连续函数f(x，y)，且f(x，y)=3(x+y)+16xy。 A.f(x，y)=3(x+y)+32xy B.f(x，y)=3(x+y)-32xy C.f(x，y)=3(x+y)-16xy D.f(x，y)=3(x+y)+16xy

4.对于函数z＝xy，原点(0，0)（ ）A．不是驻点B．是驻点但非极值点C．是驻点且为极大值点D．是驻点且为极小值点

更多“对于函数f（x，y）＝xy，原点（0，0）（　　）。 ”相关问题

  • 第1题：


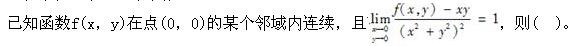    A.点(0，0)不是f(x，y)的极值点
    B.点(0，0)是f(x，y)的极大值点
    C.点(0，0)是f(x，y)的极小值点
    D.根据所给条件无法判断点(0，0)是否为f(x，y)的极值点

    答案：A
    解析：

  • 第2题：

    设函数f(x，y)=X2+Y2+xy+3，求f(x，y)的极值点与极值．


    答案：
    解析：

  • 第3题：

    设X的分布函数为F(x)=且Y=X^2－1,则E(XY)=_______.


    答案：1、-0.6
    解析：
    随机变量X的分布律为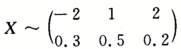，E(XY)=E【X(X^2-1)】=E（X^3-X）=E(X^3)-E(X)，因为E(X^3)=-8×0,3+1×0.5+8×0.2=-0.3,E(X)=-2X0.3+1×0.5+2×0.2=0.3，所以E(XY)=-0.6

  • 第4题：

    设函数，(u)可导，z=f(sin y-sin x)+xy，则=__________.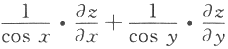


    答案：
    解析：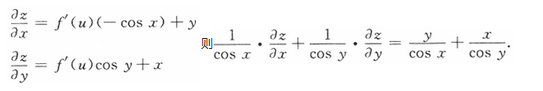

  • 第5题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第6题：

    下列函数图象与y=f（x）的图象关于原点对称的是（　　）

    A.y=-f（x）
    B.y=f（-x）
    C.y=-f（-x）
    D.y=｜f（x）｜

    答案：C
    解析：

  • 第7题：

    设函数f（x，y）＝x3+y3-3xy，则（）。

    • A、f（0，0）为极大值
    • B、f（0，0）为极小值
    • C、f（1，1）为极大值
    • D、f（1，1）为极小值

    正确答案:D

  • 第8题：

    设有关系模式R（XYZ，X→Y，Y→Z），其分解＝{XY，XZ}相对F具有（），但不保持函数依赖


    正确答案:无损连接性

  • 第9题：

    函数f（x，y）=xy（6-x-y）的极值点是（）．

    • A、（0，0）
    • B、（6，0）
    • C、（0，6）
    • D、（2，2）

    正确答案:D

  • 第10题：

    单选题
    函数f（x，y）=xy（6-x-y）的极值点是（）．
    A

    （0，0）

    B

    （6，0）

    C

    （0，6）

    D

    （2，2）


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    若函数u＝xy·f[（x＋y）/xy]，f（t）为可微函数，且满足x2∂u/∂x－y2∂u/∂y＝G（x，y）u，则G（x，y）必等于（　　）。
    A

    x＋y

    B

    x－y

    C

    x2－y2

    D

    （x＋y）2


    正确答案： C
    解析：
    令t＝（x＋y）/xy，故有u＝xyf（t），则∂u/∂x＝yf（t）＋xyf′（t）（－1/x2）＝yf（t）－yf′（t）/x，∂u/∂y＝xf（t）＋xyf′（t）（－1/y2）＝xf（t）－xf′（t）/y，则x2∂u/∂x－y2∂u/∂y＝（x－y）xyf（t）＝（x－y）u，即G（x，y）＝x－y。

  • 第12题：

    填空题
    设函数y＝f（x）由方程e2x＋y－cos（xy）＝e－1所确定，则曲线y＝f（x）在点（0，1）处的法线方程为____。

    正确答案： y-1=x/2
    解析：
    e2x＋y－cos（xy）＝e－1方程两边对x求导，得e2x＋y（2＋y′）＋sin（xy）·（y＋xy′）＝0。当x＝0时，y＝1，y′＝－2，因此，法线方程为y－1＝x/2。

  • 第13题：

    已知函数f(x,y)在点(0,0)的某个邻域内连续，且 ，则

    A.点(0,0)不是f(x,y)的极值
    B.点(0,0)是f(x,y)的极大值点
    C.点(0,0)是f(x,y)的极小值点
    D.根据所给条件无法判断点(0,0)是否为f(x,y)的极值点


    答案：A
    解析：

  • 第14题：

    对于函数z=xy，原点(0，0)（）

    A.不是函数的驻点
    B.是驻点不是极值点
    C.是驻点也是极值点
    D.无法判定是否为极值点

    答案：B
    解析：
    【考情点拨】本题考查了函数的驻点、极值点的知识点．

  • 第15题：

    设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.


    答案：
    解析：

  • 第16题：

    如果函数f(x，y)在(0，0)处连续，那么下列命题正确的是


    答案：B
    解析：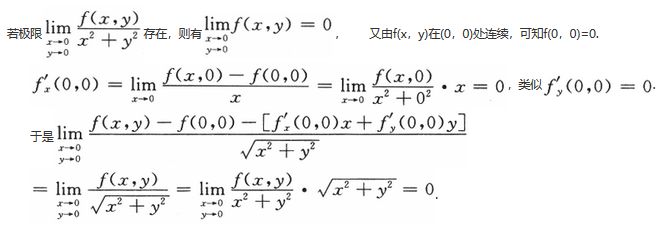

    由微分定义知f(x，y)在(0，0)处可微，故应选(B).【评注】1.本题主要考查二元函数连续、偏导数、可微的定义.
    2.可采用举反例排除错误答案.取f(x，y)=｜x｜+｜y｜排除(A)，f(x，y)=x+y排除(C)、(D).

  • 第17题：

    已知函数f(x，y)=x+y+xy，曲线C：x^2+y^2+xy=3，求f(x，y)在曲线C上的最大方向导数.


    答案：
    解析：
    【分析】函数在一点处沿梯度方向的方向导数最大，进而转化为条件最值问题
    函数f(x，y)=x+y+xy在点(x，y)处的最大方向导数为

    构造拉格朗日函数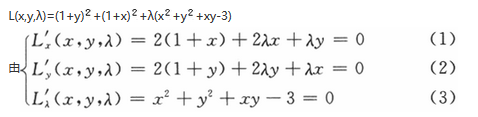

    (2)-(1)得(y-x)(2+λ)=0
    若y=x，则y=x=±1，若λ=-2，则x=-1，y=2或x=2，y=-1.
    把两个点坐标代入中，f(x，y)在曲线C上的最大方向导数为3.
    【评注】此题有一定新意，关键是转化为求条件极值问题.

  • 第18题：

    设f（x）=|x（1-x）｜，则（ ）.《》（ ）

    A.x=0是f（x）的极值点，但（0，0）不是曲线y=f（x）的拐点
    B.x=0不是f（x）的极值点，但（0，0）是曲线y=f（x）的拐点
    C.x=0是f（x）的极值点，且（0，0）是曲线y=f（x）的拐点
    D.x=0不是f（x）的极值点，（0，0）也不是曲线y=f（x）的拐点

    答案：C
    解析：

  • 第19题：

    函数f（xy，）＝xy在条件x+y＝1下的极大值为（）。

    • A、1/4
    • B、1/2
    • C、1
    • D、2

    正确答案:A

  • 第20题：

    F[x]中，有f（x）g（x）=h（x）成立，若将xy代替x可以得到什么？（）

    • A、f（xy）g（xy）=h（2xy）
    • B、f（xy）g（xy）=h（xy）
    • C、f（xy）+g（xy）=h（xy）
    • D、[fx+gx]y=hxy

    正确答案:B

  • 第21题：

    单选题
    已知函数的全微分df（x，y）＝（3x2＋4xy－y2＋1）dx＋（2x2－2xy＋3y2－1）dy，则f（x，y）等于（　　）。
    A

    x3＋2x2y－xy2＋y3＋x－y＋C

    B

    x3－2x2y＋xy2－y3＋x－y＋C

    C

    x3＋2x2y－xy2＋y3－x＋y＋C

    D

    x3＋2xy2－xy2＋y3＋x－y＋C


    正确答案： B
    解析：
    由题意知∂f/∂x＝3x2＋4xy－y2＋1，两边对x求积分，则f＝∫（∂f/∂x）dx＝x3＋2x2y－xy2＋x＋C（y），∂f/∂y＝2x2－2xy＋C′（y），又因为∂f/∂y＝2x2－2xy＋3y2－1，故C′（y）＝3y2－1，进而有C（y）＝y3－y＋C，f＝x3＋2x2y－xy2＋y3＋x－y＋C。故应选（A）。

  • 第22题：

    填空题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为____。

    正确答案： x-y=0
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第23题：

    单选题
    设函数z＝f（x，y）的全微分为dz＝xdx＋ydy，则点（0，0）（　　）。
    A

    不是f（x，y）的连续点

    B

    不是f（x，y）的极值点

    C

    是f（x，y）的极大值点

    D

    是f（x，y）的极小值点


    正确答案： D
    解析：
    函数的全微分为dz＝xdx＋ydy，则∂z/∂x＝x，∂z/∂y＝y，故∂2z/∂x2|（0，0）＝1＝A，∂2z/∂x∂y|（0，0）＝0＝B，∂2z/∂y2|（0，0）＝1＝C，又∂z/∂x|（0，0）＝0，∂z/∂y|（0，0）＝0，则B2－AC＝－1＜0，A＞0。故（0，0）是函数f（x，y）的极小值点。

相关内容