itgle.com

一平面通过两点M1(1，1，1)，M2(0，1，-1)，且垂直于平面x+y+z=0，则它的方程为( )。 A.2x+y-z=0 B.2x-y+z=0 C.x-y-z=0 D.2x-y-z=O

题目
一平面通过两点M1(1，1，1)，M2(0，1，-1)，且垂直于平面x+y+z=0，则它的方程为( )。

A.2x+y-z=0
B.2x-y+z=0
C.x-y-z=0
D.2x-y-z=O
相似考题

1.设平面经过点(1，0，－1)且与平面4x－y+2z－8=0平行，则平面π的方程为____。

2.一平面力系向点1简化时，主矢FR'≠0，主矩M1=0。若将该力系向另一点2简化，其主矢R'和主矩M2将分别为： A.可能为FR'≠0，M2≠0 B.可能为FR'=0，M2≠M1 C.可能为FR'=0，M2=M1 D.不可能为FR'≠0，M2=M1

3.平面力系向点1简化时，主矢FR'=0，主矩M1≠0，如将该力系向另一点2简化，则FR'和M2分别等于： A.FR'≠0，M2≠0 B. FR' = 0，M2≠M1C. FR'=0，M2=M1 D.FR'≠0，M2≠M1 提示:根据力系简化结果的讨论可知答案为C。

4.平面力系向点1简化时,主矢FR=0,主矩M1≠0,如将该力系向另一点2简化,则( )。A.FR≠0，M2≠0B.FR=0，M2≠M1C.FR=0，M2=M1D.FR≠0，M2=M1

参考答案和解析
答案：D
解析：
设所求平面的法向量为n=(A，B，C)，利用已知即可得出解
更多“一平面通过两点M1(1，1，1)，M2(0，1，-1)，且垂直于平面x+y+z=0，则它的方程为( )。 A.2x+y-z=0 B.2x-y+z=0 C.x-y-z=0 D.2x-y-z=O”相关问题

  • 第1题：

    曲面xyz=1上平行于x+y+z+3 =0的切平面方程是：
    A.x+y+z =0 B. x+y+z=1C.x+y+z=2 D. x+y+z=3


    答案：D
    解析：
    提示：利用两平面平行、法线向量平行、对应坐标成比例求M0坐标。

  • 第2题：

    设函数f(x)在区间［0，1］上具有2阶导数，且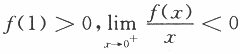，证明：
    　　(Ⅰ)方程f(x)=0在区间(0，1)内至少存在一个实根；
    　　(Ⅱ)方程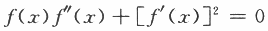在区间(0，1)内至少存在两个不同实根.


    答案：
    解析：

  • 第3题：

    已知直线L1过点M1(0，0，-1)且平行于X轴，L2过点M2(0，0，1)且垂直于XOZ平面，则到两直线等距离点的轨迹方程为( )。

    A.
    B.
    C.
    D.

    答案：D
    解析：

  • 第4题：

    一平面通过两点M1(1，1，1)，M2(0，1，-1)，且垂直于平面x+y+z=0，则它的方程为( )。

    A.2x+y-z=0
    B.2x-y+z=0
    C.x-y-z=0
    D.2x-y-z=O

    答案：D
    解析：
    设所求平面的法向量为n=(A，B，C)，利用已知即可得出解

  • 第5题：

    一平面通过点(4，-3，1)且在x，y，z轴上的截距相等，则此平面方程是( ).

    A.x+y+z+2=0
    B.x+y-z+2=0
    C.x-y+z+2=0
    D.x+y+z-2=0

    答案：D
    解析：
    由截距相等，排除 B、C ，过点(4，-3，1)=＞ D

  • 第6题：

    平面力系向点1简化时，主矢FR=0，主矩M1≠0，如将该力系向另一点2简化，则FR和M2分别等于：

    A.FR≠0，M2≠0
    B. FR = 0，M2≠M1
    C. FR=0，M2=M1
    D.FR≠0，M2≠M1

    答案：C
    解析：
    提示：根据力系简化结果的讨论可知答案为C。

  • 第7题：

    过原点(0，0，0)且垂直于向量(1，1，1)的平面方程为——．


    答案：
    解析：
    依法线向量的定义可知，所求平面的法线向量n=(1，1，1)．由于平面过原点，依照平面的点法式方程可知，所求平面方程为

  • 第8题：

    一条直线通过两点（0，0，0）和（1，1，0），另外一条直线通过两点（1，1，1）和（1，0，0），两条直线间的最短距离是（）

    • A、0.6124
    • B、0.5774
    • C、0.6014
    • D、0.5624

    正确答案:B

  • 第9题：

    一平面通过点（4，-3，1）且在x，y，z轴上的截距相等，则此平面方程是（）.

    • A、x+y+z+2=0
    • B、x+y-z+2=0
    • C、x-y+z+2=0
    • D、x+y+z-2=0

    正确答案:D

  • 第10题：

    单选题
    平面力系向点1简化时，主矢F′R=0，主矩M1≠0，如将该力系向另一点2简化，则F′R和M2分别等于：（）
    A

    F′R≠0，M2≠0

    B

    F′R=0，M2≠M1

    C

    F′R=0，M2=M1

    D

    F′R≠0，M2≠M1


    正确答案： C
    解析： 暂无解析

  • 第11题：

    多选题
    平面力系向点1简化时，主矢量R´＝0，主矩M1≠0，如将该力系向点2简化，在下列结果中，不可能出现的情形为（）。
    A

    R´≠0、M2≠0

    B

    R´＝0、M2≠M1

    C

    R´＝0、M2＝M1

    D

    R´≠0、M2＝M1


    正确答案： D,C
    解析： 暂无解析

  • 第12题：

    单选题
    已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是（　　）。
    A

    k（0，1，－1，－1）T＋（1，1，0，2）T

    B

    k（0，1，－1，－1）T＋（1，1，0，2）T/2

    C

    k（1，1，0，2）T＋（0，1，－1，－1）T

    D

    k（1，1，0，2）T＋（0，1，－1，－1）T/2


    正确答案： D
    解析：
    由Aα(→)1＝b(→)，Aα(→)2＝b(→)，故A[（α(→)1＋α(→)2）/2]＝b(→)，则（α(→)1＋α(→)2）/2是方程组AX(→)＝b(→)的特解。
    又r（A）＝3，故四元齐次方程组AX(→)＝b(→)的基础解系只含有一个解向量。由α(→)1，α(→)3是AX(→)＝b(→)的解向量，知α(→)1－α(→)3是齐次方程组AX(→)＝0(→)的解，而α(→)1－α(→)3＝（α(→)1＋α(→)2）－（α(→)2＋α(→)3）＝（0，1，－1，－1）T，故AX(→)＝b(→)的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。

  • 第13题：

    曲面x^2+cos(xy)+yz+x=0在点(0，1，-1)处的切平面方程为

    A.Ax-y+z=-2
    B.x+y+z=0
    C.x-2y+z=-3
    D.x-y-z=0

    答案：A
    解析：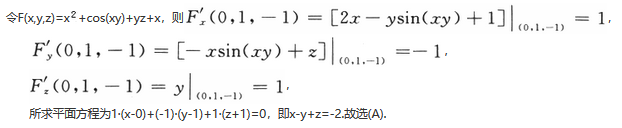

  • 第14题：

    一平面力系向点1简化时，主矢FR'≠0，主矩M1=0。若将该力系向另一点2简化，其主矢R'和主矩M2将分别为：

    A.可能为FR'≠0，M2≠0
    B.可能为FR'=0，M2≠M1
    C.可能为FR'=0，M2=M1
    D.不可能为FR'≠0，M2=M1

    答案：A
    解析：
    提示：力系的简化，主矢与简化中心无关，而主矩与简化中心有关。

  • 第15题：

    已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：



    答案：A
    解析：
    提示 求出过M1，M2，M3三点平面的法线向量。



    @##

  • 第16题：

    试求通过点Mo(一1，0，4)，垂直于平面Ⅱ：3x一4y-10=0，且与直线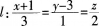
    平行的平面方程。


    答案：
    解析：
    平面Ⅱ的法向量m=（3-4，1)，直线Z的方向向量l=(3，l，2)，所以所求平面的法向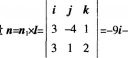

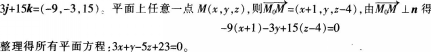
  • 第17题：

    已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称方程为（ ）。


    答案：B
    解析：
    正确答案是B。
    提示：平面π的法向量，所求直线的方向向量为i+k ,故应选B。

  • 第18题：

    已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为（ ）。


    答案：B
    解析：
    正确答案是B。
    提示：平面π的法向量，所求直线的方向向量为i+k ,故应选B。

  • 第19题：

    曲面xyz=1上平行于x+y+z+3=0的切平面方程是：（）

    • A、x+y+z=0
    • B、x+y+z=1
    • C、x+y+z=2
    • D、x+y+z=3

    正确答案:D

  • 第20题：

    过点（2，-3，1）且平行于向量a=（2，-1，3）和b=（-1，1，-2）的平面方程是（）．

    • A、-x+y+z-4=0
    • B、x-y-z-4=0
    • C、x+y+z=0
    • D、x+y-z+2=0

    正确答案:B

  • 第21题：

    单选题
    一平面力系向点1简化时，主矢F′R≠0，主矩M1=0。若将该力系向另一点2简化，其主矢R′和主矩M2将分别为：（）
    A

    可能为F′R≠0，M2≠0

    B

    可能为F′R=0，M2≠M1

    C

    可能为F′R=0，M2=M1

    D

    不可能为F′R≠0，M2=M1


    正确答案： D
    解析： 暂无解析

  • 第22题：

    单选题
    下列平面中，平行于且非重合与 坐标面yoz的平面方程是（）。
    A

    y+z+1=0

    B

    z+1=0

    C

    y+1=0

    D

    x+1=0


    正确答案： C
    解析：

  • 第23题：

    单选题
    设平面∏位于平面x－2y＋z－2＝0和平面x－2y＋z－6＝0之间，且将二平面间的距离分成1：3，则∏之方程为（　　）。
    A

    x－2y＋z－5＝0或x－2y＋z－3＝0

    B

    x＋2y＋z＋8＝0

    C

    x＋2y－4z＝0

    D

    x－2y＋z－8＝0


    正确答案： A
    解析：
    本题采用排除法较为简单。由于B、C两项所给出的平面方程的各项系数与已知平面不同，故它们与已知平面不平行，则可排除B、C项；D项平面与已知平面平行，但是不在两平面之间（可由常数项－8∉（－2，－6）判断出）。

  • 第24题：

    单选题
    过点(一1，0，1)且与平面X+Y+4z+19=0平行的平面方程为（）。
    A

    X+Y+42-3=0

    B

    2x+Y+z-3=0

    C

    X+2y+z-19=0

    D

    X+2y+42-9=0


    正确答案： B
    解析： 已知平面的法向量为n={1，1，4}，由条件可取所求平面的法向量为以={1，1，4}，所以所求平面方程为l×(x+1)+1×(y一0)+4×(z—1)=0，即x+y+4z-3=0。

相关内容