某人从远方来,他乘火车、轮船、汽车、飞机来的概率分别是0. 3、0. 2、0. 1、0. 4。如果他乘火车、轮船、汽车来的话,迟到的概率分别为1/4、1/3、1/12,而乘飞机则不会迟到。则他迟到的概率是多少?如果他迟到了,则乘火车来的概率是多少? A. 0. 10,0. 4 B. 0.15,0. 5 C. 0. 20,0.6 D. 0. 25,0.7
题目
某人从远方来,他乘火车、轮船、汽车、飞机来的概率分别是0. 3、0. 2、0. 1、0. 4。如果他乘火车、轮船、汽车来的话,迟到的概率分别为1/4、1/3、1/12,而乘飞机则不会迟到。则他迟到的概率是多少?如果他迟到了,则乘火车来的概率是多少?
A. 0. 10,0. 4
B. 0.15,0. 5
C. 0. 20,0.6
D. 0. 25,0.7
B. 0.15,0. 5
C. 0. 20,0.6
D. 0. 25,0.7
相似考题
更多“某人从远方来,他乘火车、轮船、汽车、飞机来的概率分别是0. 3、0. 2、0. 1、0. 4。如果他乘火车、轮船、汽车来的话,迟到的概率分别为1/4、1/3、1/12,而乘飞机则不会迟到。则他迟到的概率是多少?如果他迟到了,则乘火车来的概率是多少? ”相关问题
-
第1题:
设 A,B是两个事件,P(A) = 0. 3,P(B)=0. 8,则当 P(AUB)为最小值时, P(AB)=( )。
A. 0. 1 B. 0. 2 C. 0. 3 D. 0. 4答案:C解析:提示:P(AUB)取最小值,A、B之间有包含关系,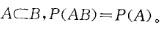
-
第2题:
设5个产品中有3个合格品、2个不合格品,从中不放回地任取2个,则取出的2 个产品中恰有1个合格品的概率为( )。
A. 0. 1 B. 0. 3
C. 0. 5 D. 0. 6答案:D解析: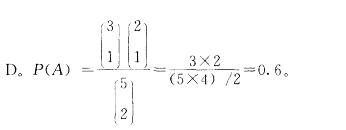
-
第3题:
甲箱中有5个正品,3个次品;乙箱中有4个正品,3个次品。从甲箱中任取3个产品放入乙箱,然后从乙箱中任取1个产品,则这个产品是正品的概率为( )。
A. 0. 176 B. 0. 2679 C. 0. 3342 D. 0. 5875答案:D解析:设B={从乙箱中取得正品},A1={从甲箱中取出3个正品},A2={从甲箱中取出2个正品1个次品},A3={从甲箱中取出1个正品2个次品},A4 ={从甲箱中取出3 个次品},显然A1、A2、A3、A4都是互斥的,所以B=B(A1 + A2+ A3+ A4)。

P(B A1) =7/10,P(B A2) =6/10,P(B A3) =5/10,P(B A4) =4/10;
故P(B) =P(BA1+BA2 + BA3+ BA4) =P(A1)P(B A1) +P(A2)P(B A2) +P(A3)P (B A3) +P(A4)P(B A4) = (10/56) x (7/10) + (30/56) x (6/10) + (15/56) x (5/ 10) + (1/56) x (4/10) =0.5875。 -
第4题:
小明在未名湖畔有一家店,出租滑冰与攀岩设备。他认为今年寒冬的概率为0. 55,暖冬的概率为0. 45。如果是寒冬,学生会租用滑冰设备在湖上滑冰,而攀岩的人将非常少。他的报酬矩阵如下:
若小明的效用函数为U(x) =ln x,写出小明期望效用,小明会把多大比例资源分配到滑冰装备上?答案:解析:小明的期望效用函数为: U(g) =0. 55ln[20 000x+5 000(l-x)]+0. 45ln[5 000r+15 000(1-x)] 整理得U(g) =0. 55ln[15 000x+5 0001+0. 45ln[15 000-10 000x] 效用最大化的一阶条件为:
解得:x=0.675。 因此,小明会把67.5%的比例资源分配到滑冰装备上。 -
第5题:
小明在未名湖畔有一家店,出租滑冰与攀岩设备。他认为今年寒冬的概率为0. 55,暖冬的概率为0. 45。如果是寒冬,学生会租用滑冰设备在湖上滑冰,而攀岩的人将非常少。他的报酬矩阵如下:
若小明为风险中性,他会把多少比例的资源分配到滑冰装备上?答案:解析:若小明为风险中性,即效用函数为线性函数,期望报酬的效用与期望效用相同。此时,期望报酬越大,期望效用越大。由(2)中结果可知,x=l时,即小明把全部资源分配到滑冰装备上,会获得最大的期望报酬和最大的期望效用。 -
第6题:
小明在未名湖畔有一家店,出租滑冰与攀岩设备。他认为今年寒冬的概率为0. 55,暖冬的概率为0. 45。如果是寒冬,学生会租用滑冰设备在湖上滑冰,而攀岩的人将非常少。他的报酬矩阵如下:
如果只出租滑冰设备,小明的期望报酬为多少?只出租攀岩设备呢?答案:解析:如果小明只出租滑冰设备,小明的期望报酬为20 000×0.55+5 000×0.45=13 250。如果小明只出租攀岩设备,期望报酬是5 000×0. 55+15 000×0.45=9 500。 -
第7题:
某系统由A、B两个部分组成,两部分工作相互独立,且两部分均失效才能导致系统失效,若A部分的失效概率为0. 2,B部分的失效概率为0. 1,则系统失效概率为( )。
A. 0. 02 B. 0. 08 C. 0. 18 D. 0. 72答案:A解析:已知A、B两部分工作相互独立,故P(系统失效)=P(A部分失效且B部分失效)=P(A部分失效)×P(B部分失效)=0.2×0. 1 =0.02。 -
第8题:
某产品可能出现A与B两种缺陷,如果出现缺陷A的概率是0.1,出现缺陷B的概率是0.2,缺陷A的发生与缺陷B的发生相互独立,则该产品无缺陷的概率是()。[2008年真题]
A. 0. 70 B. 0. 72 C. 0. 30 D. 0. 80答案:B解析:
-
第9题:
设U~N(0, 1),且 P(UA. 1是N(0,1)分布的0.8413分位数
B. 0. 8413是随机变量U超过1的概率
C. 0. 8413是随机变量U不超过1的概率
D. Φ(1) =0. 8413,并记为 u0.8413=1
E. P(U>1) =0. 1587答案:A,C,D,E解析:标准正态分布的a分位数uα满足P(X≤uα)=α,则1是N(0, 1)分布的0.8413分位数;0. 8413是随机变量U不超过1的概率;P(U0.8413= 1。由于P(U=1) =0,所以P(U>1)=1-P(u -
第10题:
某人从远方来,他乘火车、轮船、汽车、飞机来的概率分别是0.3、0.2、0.1、0.4。如果他乘火车、轮船、汽车来的话,迟到的概率分别为1/4、1/3、1/12,而乘飞机则不会迟到。则他迟到的概率是多少?如果他迟到了,则乘火车来的概率是多少()?
- A、0.10,0.4
- B、0.15,0.5
- C、0.20,0.6
- D、0.25,0.7
正确答案:B -
第11题:
某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4,且只乘一种交通工具去开会。如果他乘某种交通工具去开会的概率为0.5,请问他有可能是乘何种交通工具去开会的?
正确答案: 由于0.3+0.2=0.5,0.1+0.4=0.5,1-(0.3+0.2)=0.5,1-(0.1+0.4)=0.5,
故他有可能乘火车或轮船去开会,也有可能乘汽车或飞机去开会. -
第12题:
问答题有朋友远方来,他乘火车、轮船、汽车、飞机来的概率分别为0.3、0.2、0.1、0.4,试求: (1)他乘火车或乘飞机来的概率; (2)他不乘轮船来的概率; (3)如果他来的概率为0.5,请问他有可能是乘何种交通工具来的.正确答案: (1)他乘火车或乘飞机来的概率为0.3+0.4=0.7;
(2)他不乘轮船来的概率为1-0.2=0.8;
(3)他有可能是乘车火或轮船来,也有可能是乘汽车或飞机来.解析: 暂无解析 -
第13题:
小王开车上班需经过4个交通路口,假设经过每个路口遇到红灯的概率分别为0. 1,0.2,0.25,Q.4,则他上班经过4个路口至少有一处遇到绿灯的概率是( )。A. 0. 899
B. 0.988
C. 0. 989
D. 0. 998答案:D解析:本题属于概率问题。可以采用逆向考虑,至少有一处遇到绿灯的对立面是遇到的全是红灯,所以概率为1 -0.1 x 0.2x0. 25x0. 4 = 0. 998,所以正确答案选择D。 -
第14题:
在一批产品中,不合格率为0.1,从该批产品中随机取出5个产品,则全是不合格品的概率为( )。
A. 0. 000001 B. 0. 00001 C. 0. 001 D. 0. 1答案:B解析:全是不合格品的概率为:P=0. 15 =0.00001。 -
第15题:
甲的投篮命中率为0.8,乙为0.7。二人比赛时约定,乙投一次之后甲再投,若有一人投进而另一人未投进,则投进者胜;若二人都投进或都未投进,则比赛继续。那么乙获胜的概率约为( )。A. 0.1—0. 2
B. 0. 3—0. 4
C. 0. 4—0. 5
D. 0. 5—0. 6答案:B解析:假设只进行了一局比赛,此时乙获胜的概率为0.7 X (1-0.8) = 1 X 0.14,甲获胜的概率为0.8X(1-0.7) = 1X0.24;假设进行了两局比赛,此时乙获胜概率为 [0. 7 X 0. 8+ (1 -0. 7) X (1 -0.8) ]X 0. 7 X (1 -0.8) = 0.62 X 0.14,甲获胜的概率为 [0.7X0.8+(1 -0.7) X (1-0.8) ]X 0.8 X (1 -0. 7) = 0.62 X0. 24。由此可见,进行i+1局比赛才决出胜负,面i局比赛都没有决出胜负的概率记为Pi,则乙获胜概率为0.14Pi,甲获胜概率为0. 24Pi。故综合一切可能,乙获胜的概率为
-
第16题:
小明在未名湖畔有一家店,出租滑冰与攀岩设备。他认为今年寒冬的概率为0. 55,暖冬的概率为0. 45。如果是寒冬,学生会租用滑冰设备在湖上滑冰,而攀岩的人将非常少。他的报酬矩阵如下:
保险公司提议小明只出租滑冰装备,如果是暖冬赔给他5 000元,如果是寒冬小明付给他们5 000元,保险公司的期望报酬是多少?在什么条件下小明会接受这个提议?(写出判定式,不需要计算)答案:解析:保险公司的期望报酬是-5 000×0.45+5000×0.55=500。 小明只出租滑冰装备,在不购买保险时,期望效用为: U(g) =0. 55ln 20 000+0. 45ln 5 000 如果小明购买保险,期望效用变为: U(g)’-0.55ln(20 000-5000)+0. 45ln(5000+5000) =0. 55ln15000+0. 45ln10000 在U(g)’>U(g)的情况下,小明会接受这个提议。 -
第17题:
小明在未名湖畔有一家店,出租滑冰与攀岩设备。他认为今年寒冬的概率为0. 55,暖冬的概率为0. 45。如果是寒冬,学生会租用滑冰设备在湖上滑冰,而攀岩的人将非常少。他的报酬矩阵如下:
如果小明以x的比例把资源分配到滑冰装备上,他的期望报酬是多少?答案:解析:如果小明以z的比例资源分配到滑冰装备上,他的期望报酬是:13 250x+9 500(1-x)=3 750x+9 500,z∈[0,1] -
第18题:
妈妈给小青11.1元,让他去买5斤香蕉、4斤苹果,结果他把买的数量给弄颠倒了,从而剩下0. 6元。那么苹果每斤的售价是多少元?( )
A. 0. 9 B. 0.7 C. 0.8 D. 1答案:A解析:依题意可知,香蕉每斤的售价比苹果每斤售价多0. 6元。故苹果每斤的售价应为 (11.1- 0.6X5) / 9 = 0.9(元)。 -
第19题:
由4个元件串联组装而成的一台设备,若各元件故障的发生相互独立,每个元件正常工作的概率为0.9,则该设备正常工作的概率为( )。
A. 0. 000 1 B. 0. 656 1
C. 0. 818 1 D. 0. 999 9答案:B解析:。设备正常工作的概率为0.94。 -
第20题:
两台机床相互独立工作,需要维修的概率分别是0.3与0.2,两台机床都不需要维修的概率是()。
A. 0. 56 B. 0. 06
C. 0. 94 D. 0. 14答案:A解析:。设事件A= “甲机床需要维修”,事件B=“乙机床需要维修”,两台机床都不需要维修的概率为 P(AB) = P(A)P(B)=0. 7×0. 8=0. 56。 -
第21题:
根据Credit Risk+模型,假设一个组合的平均违约率为2%,e = 2. 72,则该组合发生4笔贷款违约的概率为( )。
A. 0. 09 B. 0. 08 C. 0. 07 D. 0. 06答案:A解析:。在一个贷款组合里,发生n笔贷款违约的概率为=e-m mn/n!,题中 e = 2. 72,组合的平均违约率为2%,则发生4笔贷款违约的概率=(2. 72 -2 X 24 )/(4 X 3 X 2 X 1)≈0. 09。 -
第22题:
某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4,且只乘一种交通工具去开会。他不乘轮船去开会的概率。
正确答案: 设他不乘轮船去开会的概率为P,
则P=1-P(A2)=1-0.2=0.8. -
第23题:
某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4,且只乘一种交通工具去开会。求他乘火车或乘飞机去开会的概率。
正确答案:记“他乘火车去开会”为事件A1,“他乘轮船去开会”为事件A2,“他乘汽车去开会”为事件A3,“他乘飞机去开会”为事件A4,这四个事件不可能同时发生,故它们是彼此互斥的.故P(A1+A4)=P(A1)+P(A4)=0.3+0.4=0.7.
