方程y'=p（x）y的通解是：

题目

方程y'=p（x）y的通解是：

相似考题

1.若 Normal 0 7.8 磅 0 2 false false false EN-US ZH-CN X-NONE MicrosoftInternetExplorer4 y1·y2为二阶线性常系数微分方程y〞+p1y＇+p2y=0的两个特解，则C1y1+C2y2（）.A.为所给方程的解，但不是通解B.为所给方程的解，但不一定是通解C.为所给方程的通解D.不为所给方程的解

2.设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x)，y2(x)，C为任意常数，则该方程通解是( )。A.C[y1(x)-y2(x)] B.y1(x)+C[y1(x)-y2(x)] C.C[y1(x)+y2(x)] D.y1(x)+C[y1(x)+y2(x)]

3.设非齐次线性微分方程y´+P(x)y=Q(x)有两个不同的解析：y1(x)与y2(x)，C为任意常数，则该方程的通解是( ).A.C[(y1(x)-y2(x)] B.y1(x)+C[(y1(x)-y2(x)] C.C[(y1(x)+y2(x)] D.y1(x)+C[(y1(x)+y2(x)]

4.已知微分方程y'+p（x）y = q（x）[q（x）≠0]有两个不同的特解y1（x）， y2（x），C为任意常数，则该微分方程的通解是： A.y=C（y1-y2） B. y=C（y1+y2） C. y=y1+C（y1+y2） D. y=y1+C（y1-y2）

更多“方程y'=p（x）y的通解是： ”相关问题

第1题：

已知y1(X)与y2(x)是方程：y" + P(x)y'+Q(x)y = 0的两个线性无关的特解，y1(x)和y2(x)分别是方程y"+P(x)y'+Q(x)y=R1(x)和y"+p(x)+Q(x)y=R2(x)的特解。那么方程y"+p(x)y'+Q(x)y=R1(x)+R2(x)的通解应是：

A. c1y1+c2y2
B. c1Y1(x) +c2Y2 (x)
C. c1y1+c2y2 +Y1(x)
D. c1y1+c2y2 +Y1 (x) +Y2 (x)

答案：D
解析：
提示：按二阶线性非齐次方程通解的结构，写出对应二阶线性齐次方程的通解和非齐次方程的一个特解，得到非齐次方程的通解。
第2题：

方程y'=f(x)y的通解是：

答案：B
解析：
提示:方程y'=f(x)y为一阶可分离变量方程。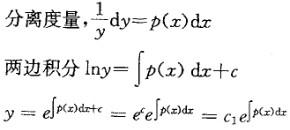
第3题：

求微分方程y"-3y'+2y=2xe^x的通解.

答案：
解析：
【解】由方程y-3y'+2y=0的特征方程解得特征根，所以方程y-3y'+2y=0的通解为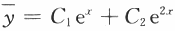
设y-3y'+2y=2xe^x的特解为y^*=x(ax+b)e^x，则(y^*)'=(ax^2+2ax+bx+b)e^x(y^*)=(ax^2+4ax+bx+2a+2b)e^x
代入原方程，解得a=-1，b=-2，故特解为：y^*=x(-x-2)e^x，所以原方程的通解为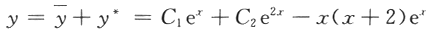
第4题：

微分方程y′=3x2的通解为y=__________．

答案：
解析：
x3+C
第5题：

求微分方程y″+3y′=3x的通解．

答案：
解析：
第6题：

单选题
微分方程dy/dx－y/x＝tan（y/x）的通解是（　　）。[2011年真题]
A
sin（y/x）＝Cx
B
cos（y/x）＝Cx
C
sin（y/x）＝x＋C
D
Cxsin（y/x）＝1

正确答案： C
解析：
令y/x＝u，则dy/dx＝xdu/dx＋u，原式等价于du/tanu＝dx/x，两边分别积分得：ln（sinu）＝lnx＋lnC，则微分方程dy/dx－y/x＝tan（y/x）的通解是sin（y/x）＝Cx。
第7题：

单选题
设非齐次线性微分方程y′＋P（x）y＝Q（x）有两个不同的解y1（x），y2（x），C为任意常数，则该方程的通解是（　　）。
A
C[y₁（x）－y₂（x）]
B
y₁（x）＋C[y₁（x）－y₂（x）]
C
C[y₁（x）＋y₂（x）]
D
y₁（x）＋C[y₁（x）＋y₂（x）]

正确答案： C
解析：
由题意可知，y(＿)＝y₁（x）－y₂（x）是y′＋P（x）y＝0的一个解，则y′＋P（x）y＝0的通解是C[y₁（x）－y₂（x）]。故所求方程通解为y₁（x）＋C[y₁（x）－y₂（x）]
第8题：

单选题
方程dy/dx＝y/x＋tan（y/x）的通解为（　　）。
A
sin（x/y）＝Cx
B
sin（y/x）＝Cx
C
sin（y/x）＝C/x
D
sin（y/x）＝x＋C

正确答案： A
解析：
原微分方程为dy/dx＝y/x＋tan（y/x）。令y/x＝u，则可变形为u＋xdu/dx＝u＋tanu，解得方程通解为sinu＝sin（y/x）＝Cx。
第9题：

单选题
设函数y1，y2，y3都是线性非齐次方程y″＋p（x）y′＋q（x）y＝f（x）的不相等的特解，则函数y＝（1－c1－c2）y1＋c1y2＋c2y3（　　）。（c1，c2为任意常数）
A
是所给方程的通解
B
不是方程的解
C
是所给方程的特解
D
可能是方程的通解，但一定不是其特解

正确答案： C
解析：
由于y₁，y₂，y₃都是y″＋p（x）y′＋q（x）y＝f（x）的不相等的特解，则y₂－y₁，y₃－y₁是它对应的齐次方程的特解，故y＝（1－c₁－c₂）y₁＋c₁y₂＋c₂y₃＝y₁＋c₁（y₂－y₁）＋c₂（y₃－y₁）是非齐次方程y″＋p（x）y′＋q（x）y＝f（x）的解，但是，由于无法确定y₂－y₁与y₃－y₁是否为线性无关，故不能肯定它是y″＋p（x）y′＋q（x）y＝f（x）的通解。
第10题：

若y1（x）是线性非齐次方程y'+p（x）y=Q（x）的一个特解，则该方程的通解是下列中哪一个方程？

答案：B
解析：
提示：非齐次方程的通解是由齐次方程的通解加非齐次方程的特解构成，令Q（x）=0，求对应齐次方程y'+p（x）y=0的通解。
第11题：

已知y1(x)和y2(x)是方程y''+p(x)y'+Q(x)y=0的两个线性无关的特解， Y1(x)和Y2 (x)分别是方程y''+p(x)y'+Q(x)y=R1(x)和y''+p(x)y'+Q(x)y=R2(x)的特解。那么方程y''+p(x)y'+Q(x)y=R1(x)y+R2(x)的通解应是：
A. c1y1+c2y2B. c1Y1(x)+c2Y2(x)
C. c1y1+c2y2+Y1(x) D. c1y1+c2y2+Y1(x)+Y2(x)

答案：D
解析：
提示:按二阶线性非齐次方程通解的结构，写出对应二阶线性齐次方程的通解和非齐次方程的一个特解，得到非齐次方程的通解。
第12题：

微分方程y′-y=0的通解为()．

A.y=ex+C
B.y=e-x+C
C.y=Cex
D.y=Ce-x

答案：C
解析：
所给方程为可分离变量方程．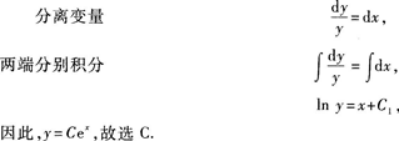
第13题：

微分方程y'+y=0的通解为y=[]

A.e-x+C
B.-e-x+C
C.Ce-x
D.Cex

答案：C
解析：
所给方程为可分离变量方程．
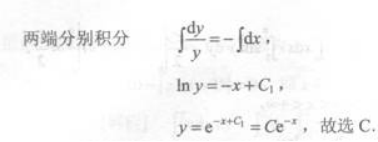
第14题：

单选题
（2012）已知微分方程y′+p+（x）y=q（x）［q（x）≠0］有两个不同的特解y1（x），y2（x），则该微分方程的通解是：（c为任意常数）（）
A
y=c（y1-y2）
B
y=c（y1+y2）
C
y=y1+c（y1+y2）
D
y=y1+c（y1-y2）

正确答案： D
解析：暂无解析
第15题：

填空题
微分方程y′＝y（1－x）/x的通解是____。

正确答案： y=Cxe^-^x
解析：
原微分方程y′＝y（1－x）/x。分离变量得dy/y＝（1/x－1）dx。两边分别积分得ln|y|＝ln|x|－x＋lnC₁，即y＝Cxe^－^x。
第16题：

单选题
已知y1（x）与y2（x）是方程y″+P（x）y′+Q（x）y=0的两个线性无关的特解，Y1（x）和Y2（x）分别是是方程y″+P（x）y′+Q（x）y=R1（x）和y″+P（x）y′+Q（x）y=R2（x）的特解。那么方程y″+P（x）y′+Q（x）y=R1（x）+R2（x）的通解应是：（）
A
c1y1+c2y2
B
c1Y1（x）+c2Y2（x）
C
c1y1+c2y2+Y1（x）
D
c1y1+c2y2+Y1（x）+Y2（x）

正确答案： A
解析：暂无解析
第17题：

单选题
函数y1（x）、y2（x）是微分方程y′＋p（x）y＝0的两个不同特解，则该方程的通解为（　　）。
A
y＝c₁y₁＋c₂y₂
B
y＝y₁＋cy₂
C
y＝y₁＋c（y₁＋y₂）
D
y＝c（y₁－y₂）

正确答案： B
解析：
由解的结构可知，y₁－y₂是该方程的一个非零特解，则方程的通解为y＝c（y₁－y₂）。

itgle.com

方程y'=p（x）y的通解是：

题目

相似考题

更多“方程y'=p（x）y的通解是： ”相关问题

相关内容