设有三元方程 ,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程A.只能确定一个具有连续偏导数的隐函数z=z(x,y) B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y) C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y) D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
题目
 ,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程
,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
相似考题
更多“设有三元方程 ,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程”相关问题
-
第1题:
已知微分方程y’+y=f(x),其中f(x)是R上的连续函数.
(Ⅰ)若f(x)=x,求方程的通解.
(Ⅱ)若f(x)是周期为T的函数,证明:方程存在唯一的以T为周期的解.答案:解析:【解】(Ⅰ)若f(x)=x,则方程为y'+y=x通解为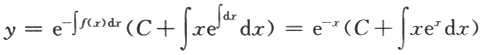
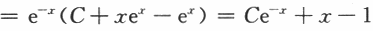
(Ⅱ)设y(x)为方程的任意解,则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T,有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0,有(e^x[y(x+T)-y(x)])'=0,
即e^x[y(x+T)=y(x)]=C.取C=0得y(x+T)-y(x)=0,
y(x)为唯一以T为周期的解. -
第2题:
 A. x=0是f(x)的极小值点
A. x=0是f(x)的极小值点
B.x=0是f(x)的极大值点
C. 曲线y=f(x)在点(0,f(0))的左侧邻域是凹的,右侧邻域是凸的
D.曲线y=f(x)在点(0,f(0))的左侧邻域是凸的,右侧邻域是凹的答案:C解析: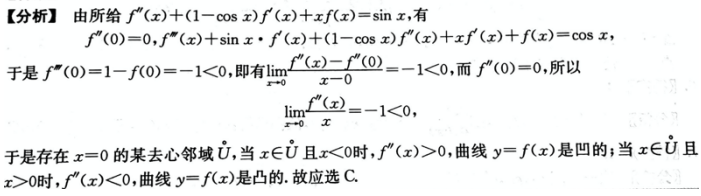
-
第3题:
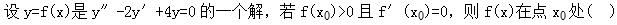 A.取得极大值
A.取得极大值
B.某邻域内单调递增
C.某邻域内单调递减
D.取得极小值答案:A解析: -
第4题:
如果曲面上任意一点都存在一个充分小的邻域,该邻域与平面上的(开)圆盘同构,即邻域与圆盘之间存在连续的1-1映射,则称该曲面为()。
正确答案:二维流形 -
第5题:
下列说法中正确的是()
- A、几个简单的势流之所以能通过简单的叠加得到一个复杂的势流,是因为势流的速度势函数是线性函数
- B、几个简单的势流之所以能通过简单的叠加得到一个复杂的势流,是因为势流的基本方程——拉普拉斯方程是线性齐次方程
- C、无环量圆柱绕流是由直线等速流与点源叠加而成的
- D、流函数存在的充分必要条件是满足连续性方程,即对于连续的平面运动,流函数总是存在的
正确答案:B,D -
第6题:
设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().
- A、取得极大值
- B、取得极小值
- C、的某个邻域内单调增加
- D、的某个邻域内单调减少
正确答案:A -
第7题:
单选题设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().A取得极大值
B取得极小值
C的某个邻域内单调增加
D的某个邻域内单调减少
正确答案: C解析: 暂无解析 -
第8题:
填空题空间一点的任意邻域内既有集合中的点,又有集合外的点,则称该点为集合的()。正确答案: 边界点解析: 暂无解析 -
第9题:
单选题设y=f(x)是y″-2y′+4y=0的一个解,若f(x0)>0且f′(x0)=0,则f(x)在点x0处( )。A取得极大值
B某邻域内单调递增
C某邻域内单调递减
D取得极小值
正确答案: D解析:
因为y=f(x)是微分方程y″-2y′+4y=0的一个解,故对于x=x0,有f″(x0)-2f′(x0)+4f(x0)=0。又因为f′(x0)=0,f(x0)>0,可得f″(x0)<0,故函数在x=x0处取极大值。故应选(A)。 -
第10题:
单选题设y=f(x)是满足微分方程y″+y′-esinx=0的解,且f′(x0)=0,则f(x)在( )。Ax0的某个邻域内单调增加
Bx0的某个邻域内单调减少
Cx0处取得极小值
Dx0处取得极大值
正确答案: B解析:
将f′(x0)=0代入方程得f″(x0)的符号,从而由极值的充分条件得正确选项。
f(x)满足方程f″(x)+f′(x)-esinx=0,所以有 -
第11题:
单选题设三元函数xy-zlny+exz=1,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程( )。A只能确定一个具有连续偏导数的隐函数z=z(x,y)
B可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
C可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
D可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
正确答案: C解析:
构造函数F(x,y,z)=xy-zlny+exz-1,则Fx′=y+zexz,Fy′=x-(z/y),Fz′=-lny+xexz。Fx′(0,1,1)=2≠0,Fy′(0,1,1)=-1≠0,Fz′(0,1,1)=0。
故根据隐函数的存在定理可知,方程xy-zlny+exz=1能确定x是y、z的具有连续偏导数的函数x=x(y,z);y是x、z的具有连续偏导数的函数y=y(x,z)。因为Fz′(0,1,1)=0不能满足定理成立的条件,故不能确定z是x、y的具有连续偏导数的隐函数z=z(x,y)。 -
第12题:
多选题下列说法中正确的是()A几个简单的势流之所以能通过简单的叠加得到一个复杂的势流,是因为势流的速度势函数是线性函数
B几个简单的势流之所以能通过简单的叠加得到一个复杂的势流,是因为势流的基本方程——拉普拉斯方程是线性齐次方程
C无环量圆柱绕流是由直线等速流与点源叠加而成的
D流函数存在的充分必要条件是满足连续性方程,即对于连续的平面运动,流函数总是存在的
正确答案: A,C解析: 暂无解析 -
第13题:
设函数f(x)在区间[0,1]上具有2阶导数,且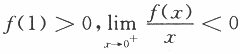 ,证明:
,证明:
(Ⅰ)方程f(x)=0在区间(0,1)内至少存在一个实根;
(Ⅱ)方程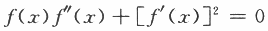 在区间(0,1)内至少存在两个不同实根.答案:解析:
在区间(0,1)内至少存在两个不同实根.答案:解析:
-
第14题:
高中“方程的根与函数的零点”(第一节课)设定的教学目标如下:
①通过对二次函数图象的描绘,了解函数零点的概念,渗透由具体到抽象思想,领会函数零点与相应方程实数根之间的关系;
②理解提出零点概念的作用,沟通函数与方程的关系。
③通过对现实问题的分析,体会用函数系统的角度去思考方程的思想,使学生理解动与静的辨证关系。掌握函数零点存在性的判断。完成下列任务:
(1)根据教学目标,设计一个问题引入,并说明设计意图;
(2)根据教学目标①,设计问题链(至少包含三个问题),并说明设计意图;
(3)根据教学目标③,给出至少一个实例和三个问题,并说明设计意图;
(4)确定本节课的教学重点;
(5)作为高中阶段的基础内容,其难点是什么
(6)本节课的教学内容对后续哪些内容的学习有直接影响答案:解析:(1)问题引入:求方程3x2+6x-l=0的实数根。
变式:解方程氩3x5+6x-l=0的实数根。(一次、二次、三次、四次方程的解都可以通过系数的四则运算,乘方与开方等运算来表示,但高于四次的方程不能用公式求解。大家课后去阅读本节后的“阅读与思考”。还有如lnx+2x-6=0的实数根很难下手,我们寻求新的角度——函数来解决这个方程的问题。)
设计意图:从学生的认知冲突中,引发学生的好奇心和求知欲,推动问题进一步的探究。通过简单的引导,让学生课后自己阅读相关内容,培养他的自学能力和更广泛的兴趣。开门见山的提出函数思想解决方程根的问题。点明本节课的目标。
(2)问题①:求方程x2-2x-3=0的实数根,并画出函数y= x2-2x-3的图象;
问题②:观察形式上函数y= x2-2x-3与相应方程x2-2x-3=0的联系。
问题③:由于形式上的联系,则方程x2-2x-3=0的实数根在函数y= x2-2x-3的图象中如何体现
设计意图:以学生熟悉二次函数图象和二次方程为平台,观察方程和函数形式上的联系,从而得到方程实数根与函数图象之间的关系。理解零点是连接函数与方程的结点。

(4)教学重点:了解函数零点的概念,体会方程的根与函数零点之间的联系,掌握函数零点存在性的判断。
(5)教学难点:准确认识零点的概念,在合情推理中让学生体会到判定定理的充分非必要性,能利用适当的方法判断零点的存在或确定零点。
(6)本节课是在学生学习了《基本初等函数(I)》的基础上,学习函数与方程的第一课时,本节课中通过对二次函数图象的绘制、分析,得到零点的概念,从而进一步探索函数零点存在性的判定。这些活动就是想让学生在了解初等函数的基础上,利用计算机描绘函数的图象,通过对函数与方程的探究,对函数有进一步的认识,解决方程根的存在性问题,为下一节《用二分法求方程的近似解》做准备。 -
第15题:
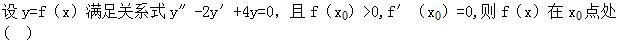 A.取得极大值
A.取得极大值
B.取得极小值
C.在xo点某邻域内单调增加
D.在xo点某邻域内单调减少答案:A解析: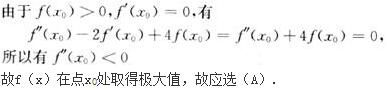
-
第16题:
空间一点的任意邻域内既有集合中的点,又有集合外的点,则称该点为集合的()。
正确答案:边界点 -
第17题:
流函数、势函数的存在条件各是什么?它们是否都满足拉普拉斯方程形式?
正确答案: 流函数存在条件是不可压缩平面流;势函数存在条件是有势流;若是不可压缩平面势流则均满足拉普拉斯方程形式 -
第18题:
以下说法正确的是()
- A、库塔-茹可夫斯基定理对流体具有普适性。
- B、如果流动存在势函数,则也存在流函数。
- C、涡量输运方程表明破坏旋涡守恒的根源是粘性作用。
- D、流层之间的内摩擦力与接触面上的压力无关。
正确答案:D -
第19题:
填空题如果曲面上任意一点都存在一个充分小的邻域,该邻域与平面上的(开)圆盘同构,即邻域与圆盘之间存在连续的1-1映射,则称该曲面为()。正确答案: 二维流形解析: 暂无解析 -
第20题:
单选题设确定了函数y=g(x),则( )。Ax=0是函数y=g(x)的驻点,且是极大值点
Bx=0是函数y=g(x)的驻点,且是极小值点
Cx=0不是函数y=g(x)的驻点
D存在x=0的一个小邻域,y=g(x)是单调的
正确答案: A解析:
g′(x)=dy/dx=(dy/dt)·(dt/dx)。dy/dt=2t/(1+t2),dx/dt=1/(1+t2)。故y′(x)=2t。又x=0时,t=0,g′(x)=0;t<0时,x<0,g′(x)<0,g(x)单调减少;t>0时,x>0,g′(x)>0,g(x)单调增加。故x=0是y=g(x)的驻点,且是极小值点。 -
第21题:
单选题函数f(x)=[cos(1/x)]/x在x=0点的任何邻域内都是( )。A有界的
B无界的
C单调增加的
D单调减少的
正确答案: B解析:
f(1/(2kπ))=2kπcos2kπ=2kπ,其中,k=±1,±2,…,故f(x)在x=0点的任何邻域内无界。 -
第22题:
单选题y=f(x)是方程y″-2y′+4y=0的一个解,若f(x0)>0,f′(x0)=0,则函数f(x)( )。A在x0点取得极大值
B在x0的某邻域单调增加
C在x0点取得极小值
D在x0的某邻域单调减少
正确答案: A解析:
由f′(x0)=0代入y″-2y′+4y=0可得y″(x0)=-4y(x0)<0。又f′(x0)=0,故函数y=f(x)在x0处取得极大值。 -
第23题:
单选题如果函数f(x)在点x0的某个邻域内恒有|f(x)|≤M(M是正数),则函数f(x)在该邻域内( )。A极限存在
B连续
C有界
D不能确定
正确答案: C解析:
由函数有界的定义可知:设函数f(x)的定义域为D,数集X∈D。如果存在数K1使得f(x)≤K1对任意x∈X都成立则称函数f(x)在X上有上界。故选C项。
