itgle.com

设A为三阶方阵,其特征值为1,－1,2,则A^2的特征值为1,1,4。()此题为判断题(对，错)。

题目
设A为三阶方阵,其特征值为1,－1,2,则A^2的特征值为1,1,4。()

此题为判断题(对，错)。

相似考题

1.设三阶矩阵A的特征值为1,1,2,则2A＋E的特征值为()。A、3，5B、1，2C、1，1，2D、3，3，5

2.设二阶矩阵A与B相似,A的特征值为－1,2,则|B|=1。()此题为判断题(对，错)。

3.设 2 是方阵 A 的特征值，则必有特征值A.0 B.1 C.-1 D.以上都不对

4.设二阶矩阵A与B相似,A的特征值为－1,2,则|B|=()A、-1B、-2C、1D、2

参考答案和解析
参考答案：正确
更多“设A为三阶方阵,其特征值为1,－1,2,则A^2的特征值为1,1,4。() ”相关问题

  • 第1题：

    设A是三阶实对称矩阵,r(A)=1,A^2－3A=O,设（1,1,-1）t为A的非零特征值对应的特征向量.(1)求A的特征值；(2)求矩阵A.


    答案：
    解析：

  • 第2题：

    问题1 已知三阶方阵A的特征值为-2，0，1，且矩阵B与A相似，则tr（B-E)的值为:

    A．0

    B．-4

    C．4

    D．-3


    令f(A)=A-3A 2 ，设α是矩阵A的属于特征值λ的特征向量，即Aα=λα，则(kA)α=(kλ)α，A m α=λ m α(其中k∈R，m∈N)，因此对任意多项式f(x)，有f(A)α=f(λ)α，即f(λ)为f(A)的特征值．即λ-3λ 2 是B=A-3A 2 的特征值．由A的特征值为-1，1，2，可知B的特征值为-4，-2，-10，且detB=-80．

  • 第3题：

    设三阶矩阵A的特征值为-1，3，4，则A的伴随矩阵的特征值为

    A．12，-4，-3

    B．-1，1/3，1/4

    C．2，5，6

    D．-1，6，9


    0，0，3

  • 第4题：

    设A为三阶方阵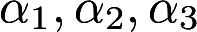，为三维线性无关列向量组，且有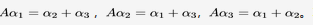求 （I）求A的全部特征值（II）A是否可以对角化？


    答案：
    解析：

  • 第5题：

    设3阶方阵A的特征值为1，-1，2，则下列矩阵中为可逆矩阵的是

    A．E-A

    B．-E-A

    C．-2E-A

    D．2E-A


    B

相关内容