itgle.com

在直角坐标系下,平面曲线f(x,y)=0可将平面分为( )个点集,当f(x,y) 大于0时,表示的点集为其正侧,至于是在曲线的外部还是内部则依赖于曲线的方向。A. 1B.2C.3D.4

题目
在直角坐标系下,平面曲线f(x,y)=0可将平面分为( )个点集,当f(x,y) 大于0时,表示的点集为其正侧,至于是在曲线的外部还是内部则依赖于曲线的方向。

A. 1

B.2

C.3

D.4

相似考题

1.在直角坐标系下,平面曲线f(x,y)=0可将平面分为___个点集,当f(x,y)大于0时,表示的点集为其正侧,至于是曲线的外部还是内部则依赖于曲线的方向。A.1B.2C.3D.4

2.设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。A、0B、π/2C、锐角D、钝角

3.曲线y=f(x)在点(x0,f(x0))有拐点,且f''(x0)存在,则f''(x0)=1。()此题为判断题(对，错)。

4.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

更多“在直角坐标系下,平面曲线f(x,y)=0可将平面分为( )个点集,当f(x,y) 大于0时,表示的点集为其正侧,至于是在曲线的外部还是内部则依赖于曲线的方向。 ”相关问题

  • 第1题：

    函数f(x)二阶可导,且f’(x0)=0,则点(x0,f(x0))为曲线y=f(x)的拐点。()

    此题为判断题(对，错)。


    参考答案：错误

  • 第2题：


    A. x=0是f(x)的极小值点
    B.x=0是f(x)的极大值点
    C. 曲线y=f(x)在点（0,f（0））的左侧邻域是凹的，右侧邻域是凸的
    D.曲线y=f(x)在点（0,f（0））的左侧邻域是凸的，右侧邻域是凹的

    答案：C
    解析：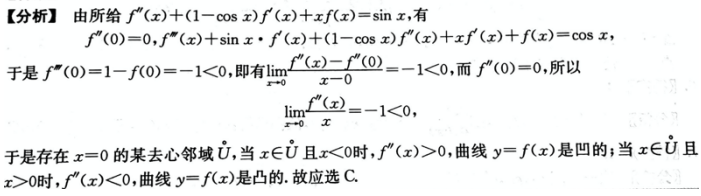

  • 第3题：

    设f（x）=|x（1-x）｜，则（ ）.《》（ ）

    A.x=0是f（x）的极值点，但（0，0）不是曲线y=f（x）的拐点
    B.x=0不是f（x）的极值点，但（0，0）是曲线y=f（x）的拐点
    C.x=0是f（x）的极值点，且（0，0）是曲线y=f（x）的拐点
    D.x=0不是f（x）的极值点，（0，0）也不是曲线y=f（x）的拐点

    答案：C
    解析：

  • 第4题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第5题：

    设y=f(x)可导，点a0=2为f(x)的极小值点，且f(2)=3，则曲线y=f(x)在点(2，3)处的切线方程为______．


    答案：
    解析：
    由于y=f(x)可导，点x0=2为f(x)的极小值点，由极值的必要条件可知f′(2)=0．曲线y=fx)在点(2，3)处的切线方程为y-3=f′(2)(x-2)=0，即y=3为所求切线方程．

相关内容