itgle.com

求解习题5.1的第1（1）题。（1）一个数的1/7与3 的差等于最大的一位数，求这个数；

题目

求解习题5.1的第1（1）题。

（1）一个数的1/7与3 的差等于最大的一位数，求这个数；

相似考题

1.有向图中顶点i的出度等于邻接矩阵中第i行中1的个数;入度等于第i列中1的个数。()此题为判断题(对，错)。

2.根据题意列出方程： （1）一个数的1/7与3 的差等于最大的一位数，求这个数； （2）从正方形的铁皮上，截去50px宽的一个长方形条，余下的面积是2000px²，那么原来的正方形铁皮的边长是多少？

3.求解习题5.1第3题。

4.已知数串1，1，2，3，5，8，13，……，从第3个数起每个数都等于它前面相邻的两个数之和，那么，数串中第1999个数被3除所得的余数是（）。A．1B．2C．3D．4

更多“求解习题5.1的第1（1）题。（1）一个数的1/7与3 的差等于最大的一位数，求这个数；”相关问题

  • 第1题：

    若有如下程序： SET TALK OFF INPUT TO X FOR i=1 TO 3 INPUT TO Y IF Y＞X X=Y ENDIF ENDFOR ?X RETURN 本程序的功能是( )。

    A．求3个数中的最大值

    B．求4个数中的最大值

    C．求3个数中的最小值

    D．求4个数中的最小值


    正确答案：B
    解析：FOR-ENDFOR语句通常用于实现循环次数已知情况下的循环结构。
    FOR-ENDFOR语句的格式为：
    FOR循环变量＞=初值＞TO终值＞[STEP步长＞]
    循环体＞
    ENDFOR|NEXT
    执行该语句时，首先将初值赋给循环变量，然后判断循环条件是否成立(若步长为正值，循环条件为 循环变量＞=终值＞；若步长为负值，循环条件为循环变量＞＞=终值＞)。若循环条件成立，则执行循环体，然后循环变量增加一个步长值，并再次判断循环条件是否成立，以确定是否再次执行循环体。若循环条件不成立，则结束该循

  • 第2题：

    ：一列数1，2，4，7，11，16，22，29，…这列数的组成规律是第2个数比第1个数多1；第3个数比第2个数多2；第4个数比第3个数多3；依此类推。那么这列数左起第1992个数除以5的余数是（ ）。

    A．0

    B．1

    C．2

    D．4


    正确答案：C
    根据这列数的组成规律，我们容易算出前l5个数被5除的余数，列表如下：


    数的序号

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

    被5除的余数

    1 2 4 2 1 1 2 4 2 1  1   2  4  2  1

     

     

    从表上可以看出，第1、2、3、4、5五个数被5除的余数，与第6、7、8、9、10五个数被5除的余数对应相同，也与第11、12、13、14、15五个数被5除的余数对应相同。因此，这一列数被5除所得的余数，每隔5个数循环出现。由于1992=5×398+2，所以第1992个数被5除的余数，与第二个数被5除的余数一样，也就是2。故本题正确答案为C。

  • 第3题：

    从1,2,…,10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120。()


    正确答案:对

  • 第4题：

    若采用邻接矩阵来存储简单有向图，则其某一个顶点i的人度等于该矩阵______。

    A．第i行中值为1的元素个数

    B．所有值为1的元素总数

    C．第i行及第i列中值为1的元素总个数

    D．第i列中值为1的元素个数


    正确答案：D

  • 第5题：

    有若干个数，第一个数记为a1，第二个数记为a2，…，第n个数记为an。若a1=1/2，从第二个数起，每个数都等于“1与它前面那个数的差的倒数”。试计算：a2=______，a3=____，a4=_____，a5=______。这排数有什么规律吗？由你发现的规律，请计算a2004是多少？


    正确答案：
    a2=2，a3=-1，a4=1/2，a5=2。这排数的规律是:1/2,2,-1循环. a2004=-1

  • 第6题：

    若采用邻接矩阵来存储简单有向图，则其某一个顶点i的入度等于该矩阵(37)。

    A．第i行中值为1的元素个数

    B．所有值为1的元素总数

    C．第i行及第i列中值为1的元素总个数

    D．第i列中值为1的元素个数


    正确答案：D
    解析：由邻接矩阵的定义可知，对于无向图，其邻接矩阵第i行元素的和即为顶点i的度。对于有向图，其邻接矩阵的第i行元素的和为顶点i的出度，而邻接矩阵的第j列元素的和为顶点j的入度。

  • 第7题：

    有10个连续奇数，第1个数等于第10个数的11/5，求第1个数？（ ）

    A．5

    B．11

    C．13

    D．15


    正确答案：D
    因为是10个连续奇数，且第一个比第10个数小，所以这10个数构成公差为2的递增等差数列。设最小项为a，则根据题意，可知：(11/5)·a=a+(10-1)× 2。解得：a=15。选D。

  • 第8题：

    一列数，前3个是1，9，9，以后每个都是它前面相邻3个数字之和除以3所得的余数，这列数中的第1999个数是几?（　　）

    A.9
    B.0
    C.1
    D.2

    答案：B
    解析：
    将这列数从前至后开始排列：1，9，9，1，1，2，1，1，1，O，2，0，2，1，0，0，1，1，…，这列数除去前面的三个数，其余每13个数为一周期。而(1999-3)÷13=153……7，周期中第7个数是0。所以选B。

  • 第9题：

    若采用邻接矩阵来存储简单有向图，则其某一个顶点i的入度等于该矩阵()。

    A.第i行中值为1的元素个数
    B.所有值为1的元素个数
    C.第i行及第i列中值为1的元素总个数
    D.第i列中值为l的元素个数

    答案：D
    解析：
    对于无向图，其邻接矩阵的第i行的和即为第i个顶点的度。对于有向图，邻接矩阵的第i行元素的和即为第i个顶点的出度，而邻接矩阵的第j列元素的和即为第j个顶点的出度。

  • 第10题：

    关系R与关系S只有一个公共属性，T1是R与S作θ连接的结果，T2是R与S自然连接的结果，则（）。

    • A、T1的属性个数等于T2的属性个数
    • B、T1的属性个数小于T2的属性个数
    • C、T1的属性个数大于或等于T2的属性个数
    • D、T1的属性个数大于T2的属性个数

    正确答案:D

  • 第11题：

    如果从1，2，…，10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120


    正确答案:正确

  • 第12题：

    问答题
    35.从1，2．3，4，5中任取3个数字，则这3个数字中不含1的概率为

    正确答案：
    解析：

  • 第13题：

    ：有一列数，第1个数是35，第2个数是25，从第3个数开始，每个数都是它前面两个数的平均数。这列数的第15个数的整数部分是（ ）。

    A．19

    B．24

    C．28

    D．30


    正确答案：C

    第3个数为(35+25)÷2=30，第4个数为(25+30)÷2=27.5，第5个数为(30+27．5)÷2=28.75，第6个数为28.125，此后每个数都小于第5个数，大于第6个数。所以第5个数的整数部分是28。因此，本题正确答案为C。

  • 第14题：

    若采用邻接矩阵来存储简单有向图，则其某一个顶点i的入度等于该矩阵______。

    A．第i行中值为1的元素个数

    B．所有值为1的元素总数

    C．第i行及第i列中值为1的元素总个数

    D．第i列中值为1的元素个数


    正确答案：D
    解析：由邻接矩阵的定义(见试题(4)的分析)可知，对于无向图，其邻接矩阵第i行元素的和即为顶点i的度。对于有向图，其邻接矩阵的第i行元素之和为顶点i的出度，而邻接矩阵的第j列元素之和为顶点j的入度。

  • 第15题：

    下面程序用“冒泡”法将数组a中的10个整数按升序排列，算法是：从数组的第1个元素开始，依次将相邻的两个数相比较(第1个数与第2个数，第2个数与第3个数……如此重复)，若前面的数较大，则这两个数交换位置。这样执行一遍后，最后一个数已经是数组中最大的数。然后将数组的前n-1个数重复上述过程。如此继续，可将数组排序，请将程序补充完整。

    Option Base 1

    Private Sub Command1_Click()

    Dim a()

    a=Array(678，45，324，528，439，387，87，875，273，823)

    Fori＝【 】

    Forj= 【 】

    If a(j)【 】a(j+1)Then

    a1=a(j)

    a(j)＝a(j+1)

    a(j+1)=al

    End lf

    Nextj

    Next i

    For i＝1 To 10

    Print a(i)

    Next i

    End Sub


    正确答案：1 To 91 To 10-I＞=或＞
    1 To 9,1 To 10-I,＞=或＞ 解析：本题主要考查了“冒泡”排序法，根据题意描述的“冒泡”法的思想，对10个数进行排序，需要进行9趟排序过程，故[10]处填1 To 9。每一趟中都需要进行一定次数的两数比较，如第一趟过程中需要对前9个数进行相邻数两两比较，第二趟中对前8个数进行相邻数两两比较，依此类推，总结规律可知 [11]处应填1To 10-i。比较中两数交换位置的前提条件是前面的数大于后面的数或大于等于后面的数。故[12]处应填＞＝或＞。

  • 第16题：

    如果一个数的平方与这个数的差等于0，那么这个数只能是（ ）

    A 0 B －1 C 1 D 0或1


    正确答案：D

  • 第17题：

    知识技能

    （1）一个正数的平方等于361，求这个正数；

    （2）一个负数的平方等于121，求这个负数；

    （3）一个数的平方等于196，求这个数。


    （1）19；    （2）-11；    （3）±14

  • 第18题：

    有10个连续奇数，第1个数等于第10个数的5/11，求第1个数？

    A、5

    B、11

    C、13

    D、15


    正确答案：D
    选D
    普通解法：设第1个数为x，则第10个数应该是x+18，x=5/11(x+18)。
    特殊解法：第1个数为第10个数的5/11，则第一个数为5的倍数，排除B、C。如果第一个数为5，则第10个数为11，显然不对。

  • 第19题：

    已知等差数列{an}中，a1=21，Sn是它的前n项之和，S7=S15。
    (1)求Sn；
    (2)这个数列的前多少项之和最大 求出最大值。


    答案：
    解析：
    (1)设等差数列的公差为d，由题意可得：



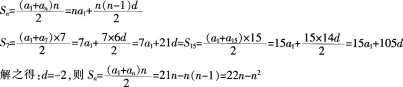
    (2)Sn=22n-n2=-(n-11)2+121，当n=11时，数列之和最大，最大值为121。

  • 第20题：

    从1、2、3、…、n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为多少？( )

    A.106
    B.107
    C.108
    D.109

    答案：C
    解析：
    根据两数之差不能为13，构造(1、14、27、40、…)、(2、15、28、41、…)、(3、16、29、42…)、…、(13、26、39、…)。显然每个括号中均不能取连续的两个数，现要求任取57个数必有两数差为13时，n的最大值，那考虑取57个可能没有两数之差为13时，凡的最小值，显然每组数中取第1、3、5、7、…个数可使n最小，相当于每26个数取前13个数，那么要取57个数，57÷13-4……5，n最小为26×4+5=109.即n为109时就能满足取57个数且可能没有两数之差为13的情况，当n为108时，必然有两个数之差为13，所以n的最大值为108，

  • 第21题：

    关系R与关系S只有1个公共属性，T1是R与S作θ连接的结果，T2是R与S作自然连接的结果，则（）。

    • A、T1的属性个数等于T2的属性个数
    • B、T1的属性个数小于T2的属性个数
    • C、T1的属性个数大于或等于T2的属性个数
    • D、T1的属性个数大于T2的属性个数

    正确答案:D

  • 第22题：

    设二个数组为A[0‥7]、B[-5‥2，3‥8]，则这两个数组分别能存放的字符的最大个数是（）。

    • A、7和35
    • B、1和5
    • C、8和48
    • D、1和6

    正确答案:C

  • 第23题：

    单选题
    有10个连续奇数，第1个数等于第10个数的5/11，求第1个数？
    A

    5

    B

    11

    C

    13

    D

    15


    正确答案： D
    解析：

相关内容