itgle.com

把一个三角形分成四个面积相等的三角形，可以怎样分？你能想出几种方法？

题目

把一个三角形分成四个面积相等的三角形，可以怎样分？你能想出几种方法？

相似考题

1.两个面积相等的三角形可以拼成一个平行四边形。此题为判断题(对，错)。

2.下列周长相等的图形中,哪一个面积最大?()A、圆形B、三角形C、正方形D、六边形

3.将直角边长为50px，100px的一个直角三角形，绕直角顶点按逆时针方向连续旋转三次，每次都旋转90°。（1）试作出每次旋转前后的三角形；（2）将所得的所有三角形看成一个图形，你将得到怎样的图形？

4.老师“教”学生:三角形的面积是“底乘高的一半”。实际上,三角形的面积是“底乘高的一半”,与老师教或者不教没有关系,即使没有人类,三角形的面积都是“底乘高的一半”。那么,作为老师,你怎么把这个科学道理给学生说清楚?从而避免一个道德上的缺陷:不要使学生以为“三角形的面积是‘底乘高的一半’是我的老师教出来的”。

参考答案和解析
此题暂无答案
更多“把一个三角形分成四个面积相等的三角形，可以怎样分？你能想出几种方法？”相关问题

  • 第1题：

    能把一个任意三角形分成面积相等的两部分是（ ）

    A.角平分线

    B.中线

    C.高

    D.A、B、C都可以


    正确答案：B

  • 第2题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形面积的（ ）。


    答案：B
    解析：
    依题意，一个正三角形和一个正六边形周长相等，所以正三角形的边长为正六边形边长的2倍，正三角形可以划分为4个边长为其一半的全等的小正三角形，正六边形可以划分为边长与其相等的6个全等的小正三角形，所以正六边形的面积为正三角形的1. 5倍。

  • 第3题：

    如图，在长方形ABCD中，已知三角形ABE、三角形ADF与四边形AECF的面积相等，则三角形AEF与三角形CEF的面积之比是


    A.5∶1
    B.5∶2
    C.5∶3
    D.2∶1

    答案：A
    解析：
    第一步，三角形ABE、三角形ADF与四边形AECF的面积相等，则三者各占长方形ABCD面积的1/3。连接辅助线AC，则三角形ACD的面积为长方形的1/2。?



    第二步，三角形ADF与三角形ACD的高相同，都为AD，三角形高相同，底边之比等于面积之比，则FD：CD＝2：3，所以CF＝1/3CD，同理CE＝1/3BC，因此三角形CEF的面积为长方形面积的1/18，则三角形AEF的面积为长方形面积的1/3－1/18＝5/18，所以两者面积之比为5：1。解法二：赋值长方形的长为6，宽为3，则长方形的面积为18。三角形ABE、三角形ADF与四边形AECF的面积相等，则三者的面积各为6。那么FD的长为4，CF长2，则CE的长为1，则三角形CEF的面积为1，三角AEF的面积为6－1＝5，则两者的面积之比为5：1。因此，选择A选项。

  • 第4题：

    若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（）。

    A.20
    B.24
    C.12
    D.6.2

    答案：B
    解析：
    两个直角边和为14，直角边中至少有一个大于等于7。根据斜边长度大于任意直角边，可知斜边大于7。则周长大于21。周长与面积相等，直接选B。

  • 第5题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的;


    A. 0.5倍
    B. l.5倍
    C. 1倍
    D. 2倍

    答案：B
    解析：
    解题指导： 本题为几何类题目。因为正三角形和一个正六边形周长相等，又正三角形与正六边形的边的个数比为1:2，所以其边长比为2:1，正六边形可以分成6个小正三角形，边长为1的小正三角形面积：边长为2的小正三角形面积=1:4。所以正六边形面积：正三角形的面积=1×6/4=1.5。故答案为B。

  • 第6题：

    如下图，把三角形ABC 的三边分别延长1、2、3 倍，得到一个新的三角形，则新三角形的面积是原三角形ABC 面积的几倍？（ ）

    A、15
    B、16
    C、17
    D、18

    答案：D
    解析：

  • 第7题：

    大断面面积计算使用的几何求积法，是把断面按河床的转折点依竖直方向划分成若干个（），然后用几何面积公式计算各部分面积及总和。

    • A、梯形或三角形
    • B、梯形
    • C、三角形
    • D、四边形

    正确答案:A

  • 第8题：

    等底等高的所有三角形面积（）。

    • A、相等
    • B、不相等
    • C、不能确定

    正确答案:A

  • 第9题：

    一个三角形和一个平行四边形，面积相等，底也相等，那么三角形和平行四边形的高相比较（）.

    • A、三角形的高是平行四边形的一半
    • B、相等
    • C、三角形的高是平行四边形的2倍

    正确答案:C

  • 第10题：

    单选题
    等底等高的所有三角形面积（）。
    A

    相等

    B

    不相等

    C

    不能确定


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    大断面面积计算使用的几何求积法，是把断面按河床的转折点依竖直方向划分成若干个（），然后用几何面积公式计算各部分面积及总和。
    A

    梯形或三角形

    B

    梯形

    C

    三角形

    D

    四边形


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    一个三角形，三个内角的度数都相等，这个三角形一定是()。
    A

    任意三角形

    B

    等腰三角形

    C

    等边三角形


    正确答案： A
    解析： 暂无解析

  • 第13题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形面积的：

    A. √2 倍
    B. 1.5 倍
    C. √3 倍
    D. 2 倍

    答案：B
    解析：
    假设正六边形和正三角形的周长均为 6，则正三角形的边长为 2，正六边形的边长为 1。正六变形可看做 6 个边长为 1 的正三角形，边长为 2 的正三角形面积是边长为 1 的正三角形面积的 4 倍，因此正六边形的面积是正三角形面积的 1.5 倍。故答案为B。

  • 第14题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：



    答案：B
    解析：
    .［解析］ 本题为几何类题目。因为正三角形和一个正六边形周长相等，又正三角形与正六边形的边的个数比为1:2，所以其边长比为2:1，正六边形可以分成6个小正三角形，边长为1的小正三角形面积：边长为2的小正三角形面积=1:4。所以正六边形面积：正三角形的面积=1×6/4=1.5。所以选B。

  • 第15题：

    将一根绳子任意分成三段,则此三段能构成一个三角形的概率是：


    答案：A
    解析：
    第一步，本题考查概率问题，需结合几何性质解题。
    第二步，设线段长度为a，任意分成三段长分别为x，y和a-x-y，显然有x＞0，y＞0，a－x－y＞0，将这三个约束条件画到（x，y）二维平面坐标系上，这三条直线围成了一个直角三角形即为可行域，其面积为1/2a2。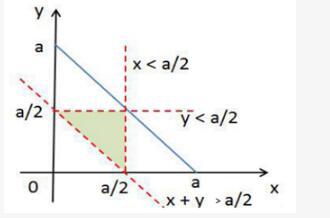

  • 第16题：

    一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：



    A.√2倍
    B.1.5倍
    C. √3倍
    D.2倍

    答案：B
    解析：
    .［解析］ 本题为几何类题目。因为正三角形和一个正六边形周长相等，又正三角形与正六边形的边的个数比为1:2，所以其边长比为2:1，正六边形可以分成6个小正三角形，边长为1的小正三角形面积：边长为2的小正三角形面积=1:4。所以正六边形面积：正三角形的面积=1×6/4=1.5。所以选B。

  • 第17题：

    案例
    下面是两位教师关于《等边三角形》的教学过程

    教师甲
    教师乙

    (1)复习等腰三角形的性质及判定方法。
    教师提问、学生思考：边怎样 角怎样 对称性呢
    (2)等边三角形性质的教学。
    教师提问、学生思考：
    ①什么样的三角形叫等边三角形
    ②等边三角形的三个内角都相等吗
    ③等边三角形是轴对称图形吗
    (3>等边三角形判定的教学
    师：哪位同学说说我们应从什么角度来考虑等边三角形
    的判定方法
    生：从角和边来考虑。(教师希望的答案是从边和角来考
    虑)
    师：那你能说一下等边三角形有怎样的判定方法吗
    生：从角来说，我认为三个内角都是600的三角形是等边
    三角形(学生的回答出乎老师的预设，打乱了PPT的放
    映程序)
    师：关于边的研究比较简单，我们还是从边开始探讨吧。
    生：好。(学生没有异议，只能跟着老师的要求回答问题，
    继续学习)
    (1)复习引入
    ①理解等腰三角形的定义、性质；
    ②观察生活中的等边三角形，引出课题。
    (2)新课教学
    ①等边三角形有什么性质
    (PPT显示)可以从边、角、对称性来考虑
    设计活动1：
    学生拿出课前准备的等边三角形纸片，认真折叠并
    观察，小组合作，互相探讨，一个小组代表发表自己
    组的观点．其他小组补充，最后一起归纳总结。
    ②等边三角形的判定方法有哪些 设计开放性提问
    (唧’显示)
    你认为怎样才能说明三角形是等边三角形 等腰三
    角形怎样变化才能说明是等边三角形
    设计活动2：
    小组合作，互相探讨，教师操作几何画板，学生也上
    台操作几何画板，观察等腰三角形满足什么条件后
    成为等边三角形。学生积极主动地参与课堂学习，能
    够在折纸操作后很快说出等边三角形的性质和判定
    方法．通过操作几何画板形象地展现变化过程。新知
    识的获得和掌握很快且水到渠成，最后教师和学生
    一起归纳总结。
    问题：
    请从下列三个方面对甲乙两位教师的教学过程进行评价：
    (1)引入的特点；(6分)
    (2)教师教的方式；(7分)+
    (3)学生学的方式。(7分)


    答案：
    解析：
    (1)甲教师的引入存在优点也存在缺陷。优点是一开始复习了上节内容，巩固旧识，但是并没有进行新旧知识间的衔接过渡．没有达到降低学生对新知识的认知难度的目的。
    乙教师的引人存在优点也存在缺陷。优点是一开始复习了上节内容，巩固旧知识。并联系生活实际让学生观察等边三角形的特点．降低学生对新知识的认知难度。但是在巩固旧知识时并没有合理地进行新旧知识之间的衔接过渡，使学生对等边三角形与等腰三角形之间的关系没有得到一个初步的感官认识。
    (2)甲教师的教学方法存在优点也存在缺陷，在教学开始开门见山地介绍本节课题，抛出问题：(!)什么样的三角形叫等边三角形 ②等边三角形的三个内角都相等吗 ③等边三角形是轴对称图形吗 引起学生的有意注意，使学生迅速进入学习状态，对本节内容的基本轮廓有了大致了解，但是没有进行合理的情境创设，将知识全盘塞给学生，剥夺了学生发现问题、提出问题进而解决问题的过程。无法激发学生学习新知识的兴趣，学生只能机械地配合教师教学。在进行等边三角形判定的教学过程中，教师没有做好充分的课前准备，预设学生在课堂中提出各种问题的突发情况，采取回避方式来应对学生提出“从角来说，我认为三个内角都是60。的三角形是等边三角形”，这不符合新课程标准中对教师的要求。限制学生思维，扼杀学生探求真理的欲望，不利于学生的成长。
    乙教师的教学方法存在优点也存在缺陷。优点是充分发挥了学生的主动性，动手操作，小组合作探究，开放性问题等环节的设置．激发了学生开动脑筋自主探究的兴趣并能够调动学生参与到课堂教学活动的积极性。缺点在于教师对“等边三角形有什么性质 ”这一开放性问题的提出并不能充分突出“等边三角形”这节的核心——通过与等腰三角形性质的探究过程迁移到对等边三角形性质的探究。为第二个开放性问题的解决造成了一定的阻碍。
    (3)甲教师的学生在学习过程中，只是在机械地配合教师的提问，完成本节课的教学。甲教师在日常教学过程中没有注意培养学生善于思考、提出问题、发现问题、解决问题的良好习惯。导致学生学习的积极性不高，对学习内容存在疑问也不会及时提出。
    乙教师的学生在学习过程中，动手操作能力、合作探究意识均很强。学习积极性高，对学习过程中存在的疑问能够及时提出，并善于通过自主探究合作交流解决问题。

  • 第18题：

    周长相等的等边三角形、正方形、圆形，哪一个的面积最大？


    正确答案: 圆形

  • 第19题：

    周长相等的等边三角形、正方形、圆形，（）的面积最大。


    正确答案:圆形

  • 第20题：

    一个三角形，三个内角的度数都相等，这个三角形一定是（）。

    • A、任意三角形
    • B、等腰三角形
    • C、等边三角形

    正确答案:C

  • 第21题：

    编一个程序，定义一个类，该类中定义二个非静态方法，一个方法用来求出这个三角形的周长，另一个方法用来求出这个三角形的面积。已知三角形三条边a，b，c，计算其面积可以用Math类中的Sqrt（）方法，有表达式Math.Sqrt（s*（s-a）*（s-b）*（s-c）），可以利用它计算指定数的开方，其中s=（a+b+c）/2。在主方法中输入一个三角形三条边a，b，c，要求调用这二个非静态方法计算三角形的周长和面积。注意：在输入三角形三条边时，必须检查它们的数据合法性。


    正确答案: class triangle { public double c(double a, double b, double c) { double zc; zc = a + b + c; return zc; } public double s(double a, double b, double c) { double mj,s1; s1 = (a + b + c) / 2; mj = Math.Sqrt(s1*(s1-a)*(s1-b)*(s1-c)); return mj; } } class Program { static void Main(string[] args) { triangle tr=new triangle (); double x, y, z; Console.WriteLine(/请输入三角形的三边/); x = double.Parse(Console.ReadLine()); y = double.Parse(Console.ReadLine()); z = double.Parse(Console.ReadLine()); if ((x + y > z && x - y < z) && (x + z > y && x - z < y) && ((y + z) > x && (y - z < x))) { Console.WriteLine(/三角形的周长为{0}/, tr.c(x, y, z)); Console.WriteLine(/三角形的面积为{0}/, tr.s(x, y, z)); } else Console.WriteLine(/三角形三边不合法/);

  • 第22题：

    单选题
    已知三角形内的一个点到它的三边距离相等，那么这个点是（　　）．
    A

    三角形的外心

    B

    三角形的重心

    C

    三角形的内心

    D

    三角形的垂心


    正确答案： D
    解析： 暂无解析

  • 第23题：

    问答题
    请认真阅读下列材料，并按要求作答。三角形的面积学生A:怎样算出红领巾的面积呢？学生B:能不能把三角形也转化成学过的……我们试一试。学生C:用两个一样的直角三角形可以拼出……学生B:哇！用两个同样的三角形可以拼出一个……根据实验的结果。你能自己写出三角形面积的计算公式吗？三角形的面积=?如果用s表示三角形的面积，用a和h分别表示三角形的底和高，那么三角形面积的计算公式可以写成：S= ah÷2红领巾的底是100cm，高是33cm，它的面积是多少平方厘米？S=ah÷2=100x33÷2=？请根据上述材料完成下列任务：(1)试给出三角形面积公式的推导方法，并说明这种方法体现了什么数学思想。（10分）(2)若指导高学段小学生学习本课内容，试确定教学目标和重难点。（10分）(3)根据确定的教学目标和重难点设计新课的导入环节，并简要说明理由。(10分)

    正确答案：
    解析：

相关内容