鸡兔同笼,共有30个头,88只脚。求笼中鸡兔各有多少只?
题目
鸡兔同笼,共有30个头,88只脚。求笼中鸡兔各有多少只?
相似考题
更多“鸡兔同笼,共有30个头,88只脚。求笼中鸡兔各有多少只?”相关问题
-
第1题:
鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足。问鸡兔各几何。”
-
第2题:
一些奇异的动物在草坪上聚会,有独角兽(1个头、1只脚)、双头龙(2个头、4只脚)、三脚猫(1个头、3只脚)和四脚蛇(1个头、4只脚)。如果草坪上的动物共有58个头、160只脚,且四脚蛇的数量刚好为双头龙数量的2倍,那么有几只独角兽参加聚会?( ) A.7只 B.9只 C.15只 D.24只
正确答案:A
由“四脚蛇的数量刚好为双头龙数量的2倍”可知,将2只四脚蛇和1只双头龙捆绑在一起,共有4个头和12只脚,刚好为4只三脚猫的头脚数,故原有的动物可以看成只有两种:一种1个头1只脚(独角兽),一种1个头3只脚,则由鸡兔同笼公式
可知,参加聚会的独角兽数量为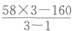 =7只。故选A。
=7只。故选A。
-
第3题:
“鸡兔同笼,共有8个头,22条腿,问鸡兔各有几只 ”这个问题,可以这样做:如果8只都是兔子,那么一共要有8×4=32条腿,比已知多了32-22=10条腿,所以鸡就有10÷2=5只,这种解决问题的方法是( )。A.枚举法
B.综合法
C.反证法
D.假设法答案:D解析:假设法,当某一变因素的存在形式限定在有限种可能时,假设该因素处于某种情况.并以此为条件进行推理。 -
第4题:
小学数学《鸡兔同笼》
一、考题回顾

 答案:解析:二、考题解析
答案:解析:二、考题解析
【教学过程】
(一)导入新知
教师:同学们,大约一千五百多年前,我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
出示主题图:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?

教师:从题中获取信息,你知道了什么,要求什么问题?
(二)讲解新知
1.尝试解决,交流想法。
问题:同学们想一想,算一算鸡和兔各有多少只?
2.感受化繁为简的必要性。
大家在刚才猜了好几组数据,经过验证都不正确,为什么猜不对呢?
例1.“笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?”
教师:从题中你们能获取哪些信息?和生活常识联系在一起,你还能说出哪些信息?
3.猜想验证。
教师:有了这些信息,我们先来猜猜,笼子可能会有几只鸡?几只兔?猜测需要抓住哪个条件?
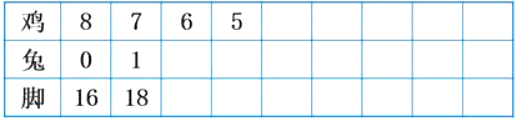
学生汇报。
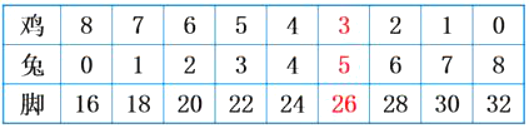
小结:这个方法挺好,能帮我们解决鸡兔同笼的问题,我们把这种方法叫做列表法。(板书:列表法)
小组讨论上表中数量之间一些数学规律,汇报。
4.数形结合理解假设法。
(1)假设全是鸡。
教师:我们先看表格中左起的第一列,8和0是什么意思?

(2)假设全是兔。
教师:我们再回到表格中,看看右起第一列中的0和8是什么意思?

(3)提出假设法概念。
刚才我们通过假设都是鸡或都是兔来解决例1的,所以把这种方法叫做假设法。这是解决“鸡兔同笼”问题的一种基本方法,也是算术方法中较为普遍的一般方法。
(板书:假设法)
(三)应用新知
利用两种方法解决古代数学问题:
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
(四)小结作业
小结:总结解决古代著名的“鸡兔同笼”问题的两种方法(列表法和假设法)
作业:课后查阅数学名著《孙子算经》,找一找其他相关的数学问题,试着解决问题。
【板书设计】
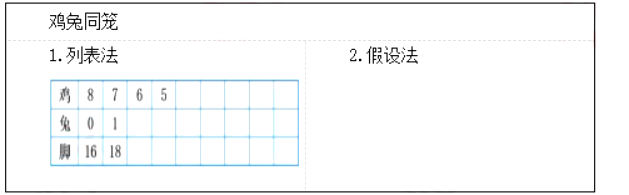
【答辩题目解析】
1.解决鸡兔同笼问题有哪些方法?
【参考答案】
列表法;假设法,分为假设全是鸡和假设全是兔子两种情况;以及方程法等.
2.你的课堂中哪个环节体现了学生的独立思考?
【参考答案】
在新课导入部分,引导学生思考理解题干的含义,培养学生的独立思考的能力;在新课部分,设置小组交流,培养学生的合作交流和独立思考的能力,感受列表法的一般性和注意事项。其次在应用新知部分,引导学生独立自主解决问题,体现了学生的独立思考。 -
第5题:
有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。求笼中各有几只鸡和兔?()
- A、鸡有23只,兔有12只
- B、鸡有12只,兔有23只
- C、鸡有20只,兔有15只
- D、鸡有15只,兔有20只
正确答案:A -
第6题:
鸡兔同笼的算法是采用经典算法之穷举法解决的
正确答案:正确 -
第7题:
对于鸡兔同笼问题,小明分析如下:设鸡兔共有x只头,y只脚,则鸡+兔=x,2鸡+4兔=y;计算出鸡=(4x-y)/2只,兔=(y-2x)/2只。这种求解问题的方法属于()。
- A、枚举法
- B、解析法
- C、递归法
- D、递推法
正确答案:B -
第8题:
一次,我在上四年级的一节活动课“鸡兔同笼”问题时,当我讲到“鸡兔共有16个头,44只脚,问鸡兔各有多少只?”时,我就按照教材上的方法进行讲解,正当学生听得认真的时候,突然听到最后一排一个“调皮鬼”在小声嘀咕着:“这样想太繁琐了,把每只兔子都砍掉两只脚,每只鸡都砍掉一只脚不就得了。”我听了开始一愣,但马上心一动,立即让他走上讲台进行讲解:“鸡和兔共有44只脚,每只兔子砍去两只脚,每只鸡砍去一只脚,44只脚就少了一半即22只脚。这22只脚由两部分组成,一部分是16只,假设是鸡的数,另一部分就是兔子的数:22-16=6只”。请用有关知识分析该教师的做法。
正确答案:教师在课堂教育教学过程中要树立“以生为本,育人为本”的思想,尊重学生人格,尊重学生的不同观点。对于同一个问题,不同的学生会有不同的想法和思路,教师应当积极关注课堂教学中学生的独特想法,有价值的思想可以全班分享,比如本案例中学生提出的简单快捷的解题思路,值得全班同学学习。教师在课堂教学中,应用心倾听、及时激起和充分肯定每一位学生的智慧火花,在这个案例中,由于教师捕捉到的信息“价值不菲”,从而激活了其他学生的思维,迸发了智慧的火花。这样的做法不仅有利于增强学生的自信和创造力,而且有利于真正实现教学相长。 -
第9题:
8051单片机DIP封装共有40只引脚,其中电源与地线引脚分别是()
- A、10脚、30脚
- B、20脚、40脚
- C、30脚、10脚
- D、40脚、20脚
正确答案:D -
第10题:
判断题最早研究鸡兔同笼问题的人毕达哥拉斯。A对
B错
正确答案: 错解析: 暂无解析 -
第11题:
多选题鸡兔同笼问题可以是很多实际的问题如()A孙子算经中的鸡兔同笼问题
B大人小孩吃面包问题
C大小油瓶装油问题
D计算素数和问题
正确答案: A,C解析: 暂无解析 -
第12题:
单选题对于鸡兔同笼问题,小明分析如下:设鸡兔共有x只头,y只脚,则鸡+兔=x,2鸡+4兔=y;计算出鸡=(4x-y)/2只,兔=(y-2x)/2只。这种求解问题的方法属于()。A枚举法
B解析法
C递归法
D递推法
正确答案: B解析: 暂无解析 -
第13题:
我国古代数字著作《孙子算法》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足。问鸡兔各几何。”你能用二元一次方程组表示题中的数量关系吗?试找出问题的解。
-
第14题:
:鸡与兔共有300只,鸡与兔的脚共有960只,问鸡与兔各有多少只?( )
A.180120
B.200100
C.120180
D.140.160
正确答案:C假设鸡有x只,那么兔有(300一x)只,由题意可知2x+4×(300一x);960,x=120,最后可知鸡有120(只),兔有300~120=180(只),故选C。 -
第15题:
请画出利用穷举法解决鸡兔同笼问题的流程图。
鸡兔同笼问题:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何答案:解析: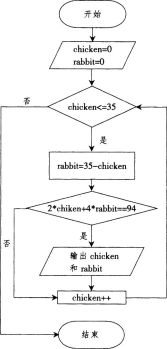
-
第16题:
“鸡兔同笼”是我国民间流传的诗歌形式的数学题,“鸡兔同笼不知数,三十六头笼中露,看来脚有100只,几只鸡儿几只兔 ”解决此问题,设鸡为x只,兔为y只,所列方程组正确的是( ). 答案:A解析:
答案:A解析: -
第17题:
鸡兔同笼问题若是转化为数学应用题,可以使用数学的()来解决。
- A、求最大值方法
- B、四舍五入方法
- C、解方程组法
- D、比较大小法
正确答案:C -
第18题:
最早研究鸡兔同笼问题的人毕达哥拉斯。
正确答案:错误 -
第19题:
数据结构与算法里,for循环嵌套for循环可解决孙子算经中提到的鸡兔同笼问题。
正确答案:正确 -
第20题:
教学设计题: 请认真阅读下述材料,并按要求作答。 《孙子算经》中有一道非常有名的题目"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"请根据给出例题设计鸡兔同笼问题的讲解:今有鸡兔同笼,上有一十二头,下有三十足,问鸡兔各几何? 试分析鸡兔同笼问题的解题规律。
正确答案:解答鸡兔问题一般采用假设法,假设全是一种动物(如全是"鸡"或全是"兔",然后根据出现的腿数差,可推算出某一种的头数。
解题规律:(总腿数-鸡腿数×总头数)÷一只鸡兔腿数的差=兔子只数
兔子只数=(总腿数-2×总头数)÷2
如果假设全是兔子,则有:鸡的只数=(4×总头数-总腿数)-2;兔的头数=总头数-鸡的只数。 -
第21题:
单选题有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。求笼中各有几只鸡和兔?()A鸡有23只,兔有12只
B鸡有12只,兔有23只
C鸡有20只,兔有15只
D鸡有15只,兔有20只
正确答案: A解析: 暂无解析 -
第22题:
问答题教学设计题: 请认真阅读下述材料,并按要求作答。 《孙子算经》中有一道非常有名的题目"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"请根据给出例题设计鸡兔同笼问题的讲解:今有鸡兔同笼,上有一十二头,下有三十足,问鸡兔各几何? 试分析鸡兔同笼问题的解题规律。正确答案: 解答鸡兔问题一般采用假设法,假设全是一种动物(如全是"鸡"或全是"兔",然后根据出现的腿数差,可推算出某一种的头数。
解题规律:(总腿数-鸡腿数×总头数)÷一只鸡兔腿数的差=兔子只数
兔子只数=(总腿数-2×总头数)÷2
如果假设全是兔子,则有:鸡的只数=(4×总头数-总腿数)-2;兔的头数=总头数-鸡的只数。解析: 暂无解析 -
第23题:
单选题鸡兔同笼问题若是转化为数学应用题,可以使用数学的()来解决。A求最大值方法
B四舍五入方法
C解方程组法
D比较大小法
正确答案: D解析: 暂无解析
