itgle.com

如图，长方形ABCD的两条边长分别为8m和6m，四边形OEFG的面积是4m2，则阴影部分的面积为（）。A.32m2 B.28m2 C.24m2 D.20m2

题目
如图，长方形ABCD的两条边长分别为8m和6m，四边形OEFG的面积是4m2，则阴影部分的面积为（）。


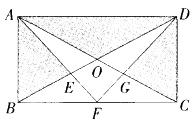
A.32m2
B.28m2
C.24m2
D.20m2
相似考题

1.如图，两个正方形的边长分别是8厘米和4厘米，则阴影部分的面积是____平方厘米。

2.如图，长方形ABCD的面积是1，M是AD的中点，N在AB边上，且AN=1/2BN。那么，阴影部分的面积等于（）。A. 1/2 B. 1/3 C. 5/12 D. 7/11

3.如图所示，BC=6，AC=8，两个等圆外切，A、B分别为两圆的圆心，则图中阴影部分的面积为：A.(25/4)π B.(25/8)π C.(25/16)π D.(25/32)π

4.如图，甲、乙、丙、丁四个长方形拼成正方形 EFGH，中间阴影为正方形。已知，甲、乙、丙、丁四个长方形面积的和是 32cm2，四边形 ABCD 的面积是 20cm2。问甲、乙、丙、丁四个长方形周长的总和是( )。（图略）A.32cmB.56cmC.48cmD.68cm

更多“如图，长方形ABCD的两条边长分别为8m和6m，四边形OEFG的面积是4m2，则阴影部分的面积为（）。 ”相关问题

  • 第1题：

    在长方形中，放人8个形状、大小相同的长方形，位置 和尺寸如图所示（图中长度单位:厘米）,则阴影部分的面积为（）。


    A.18平方厘米
    B.28平方厘米
    C.32平方厘米
    D.40平方厘米

    答案：C
    解析：
    设每个小长方形的长为x厘米，宽为y厘米。根据题意得

  • 第2题：

    如图所示，长方形卡纸的长为33．12cm，利用图中的阴影部分正好能做成一个圆柱体(接头忽略不计，π取3．14)。则这个圆柱体的表面积为______。


    答案：
    解析：
    502．4cm2。解析：设该圆柱体的半径为r，则2r+2πr=33．12，解得r=4，圆柱的高h=4r=16，故该圆柱均表面积S=2πr2+2πrh=502．4cm2。

  • 第3题：

    如图，在长方形ABCD中，已知三角形ABE、三角形ADF与四边形AECF的面积相等，则三角形AEF与三角形CEF的面积之比是


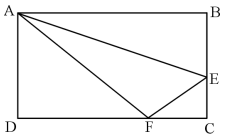    A.5∶1
    B.5∶2
    C.5∶3
    D.2∶1

    答案：A
    解析：
    第一步，三角形ABE、三角形ADF与四边形AECF的面积相等，则三者各占长方形ABCD面积的1/3。连接辅助线AC，则三角形ACD的面积为长方形的1/2。?



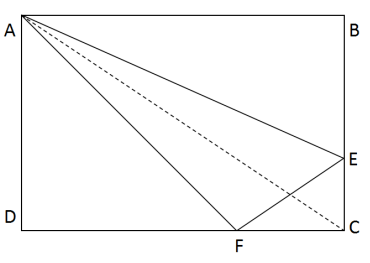
    第二步，三角形ADF与三角形ACD的高相同，都为AD，三角形高相同，底边之比等于面积之比，则FD：CD＝2：3，所以CF＝1/3CD，同理CE＝1/3BC，因此三角形CEF的面积为长方形面积的1/18，则三角形AEF的面积为长方形面积的1/3－1/18＝5/18，所以两者面积之比为5：1。解法二：赋值长方形的长为6，宽为3，则长方形的面积为18。三角形ABE、三角形ADF与四边形AECF的面积相等，则三者的面积各为6。那么FD的长为4，CF长2，则CE的长为1，则三角形CEF的面积为1，三角AEF的面积为6－1＝5，则两者的面积之比为5：1。因此，选择A选项。

  • 第4题：

    如图所示，矩形ABCD的面积为1,E、F、G、H分别为四条边的中点，FI的长度是IE的两倍，问阴影部分的面积为多少？




    答案：B
    解析：
    解题指导： 作辅助线。连接FG、EH。那么平行四边形EFGH的面积为矩形ABCD的一半，三角形GIH的面积又是平行四边形EFGH面积的一半，所以因应面积为1/4。故答案为B。

  • 第5题：

    在右图的长方形中，长和宽分别是6cm和4cm，阴影部分的面积和是 IOcm2，四边形ABCD的面积为（ ）平方厘米。
    A. 2 B. 4C. 5 D. 8


    答案：B
    解析：
    SAAGF = 4X6 + 2 = 12(cm2)，它与阴影部分的面积和是 12 + 10 = 22(cm2)，而五达形HCEFG的面积是长方形HEFG的等于4X6x "=18(cm2)，所以四边形ABCD 的面积是 22 — 18 = 4(cm2)。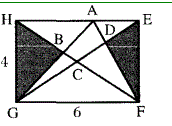

  • 第6题：

    一个箱子的底部由5块正方形纸板 ABCDE和1块长方形纸板F拼接而成（如图所示）,已知A、B两块纸板的面积比是1:16,假设A纸板的边长为2厘米,则该箱子底部的面积为（ ）平方厘米。


    A.200
    B.320
    C.360
    D.420

    答案：C
    解析：
    第一步，本题为几何问题。第二步，A、B面积之比是1:16，则边长之比是1:4，A的边长为2，可知B的边长为8。各线段长度标注在图形上如下：



    第三步，可知整个底部的面积是（10+8）×（8+6+6）=18×20=360。因此，选择C选项。

  • 第7题：

    如图6-11所示,在长方形ABCD中,三角形AOB是直角三角形且面积为54,OD=16,那么长方形ABCD的面积为（ ）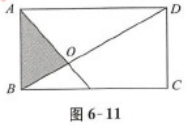

    A.150
    B.200
    C.300
    D.340
    E.380

    答案：C
    解析：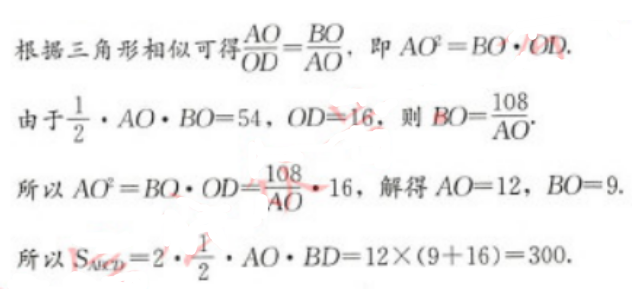

  • 第8题：

    如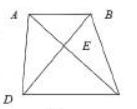，在四边形ABCD中，AB//CD，AB与CD的边长分别为4和8，若ABE的面积为4，则四边形ABCD的面积为（ ）

    A.24
    B.30
    C.32
    D.36
    E.40

    答案：D
    解析：

  • 第9题：

    图6-18是一个边长为10的正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,则阴影部分的面积为（ ）




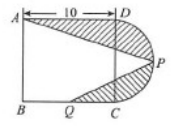
    答案：C
    解析：

  • 第10题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )

    A. 11.75 B. 16.45 C. 19.625 D. 39.25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。
    由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10X10X2，所以大半圆的面积是1/2x1/4xπx10x10x2 = 25π(平方厘米)；
    小半圆的面积是1/2πx5x5 = 12. 5π(平方厘米)；
    阴影的面积是25π-12. 5π=12. 5π=39. 25(平方厘米)。
    故本題选D。

  • 第11题：

    如图，平行四边形ABCD的面积是54平方厘米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上的任意一点，则阴影部分的面积为（ ）平方厘米。


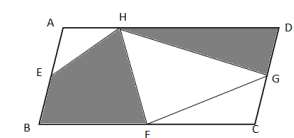    A. 27
    B. 28
    C. 32
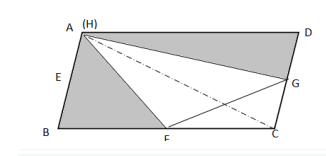
    D. 36

    答案：A
    解析：
    方法一：如图所示，由于H为AD边上的任意一点，假设H点与A点重叠，则左边阴影为三角形ABF，其面积为三角形ABC的一半；右边阴影为三角形ADG，其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半，平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。



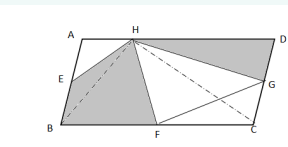
    方法二：如图所示，连接BH和CH，由于点E、F、G分别是平行四边形ABCD边上的中点，则三角形AEH和BEH相等，三角形BFH和CFH相等，三角形CGH和DGH相等，因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。

  • 第12题：

    有一个长方形，它的长为8m，宽为6m，求它的面积？


    正确答案: S=8×6
    =48m2

  • 第13题：

    在长方形A BCD中，放人8个形状、大小相同的长方形，位置和尺寸如图所示（图中长度单位：厘米），则阴影部分的面积为（）。

    A.18平方厘米
    B.28平方厘米
    C.32平方厘米
    D.40平方厘米


    答案：C
    解析：
    设每个小长方形的长为x厘米，宽为y厘米。根据题意得

  • 第14题：

    如图，平面四边形ABCD中，AB=2，BC=4，CD=5，DA=3，
    (1)若∠B与∠D互补，求AC2的值；
    (2)求平面四边形ABCD面积的最大值。


    答案：
    解析：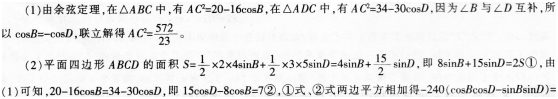

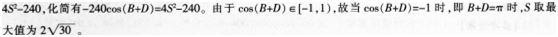
  • 第15题：

    如图，已知图中四边形两条边的长度和三个角的度数，四边形ABCD的面积是______cm2。


    答案：
    解析：
    24。解析：延长AD和BC交于点E，则得到两个等腰直角三角形△ABE和△DCE，四边形ABCD

  • 第16题：

    如图所示，矩形ABCD的面积为1，E、F、G、H分别为四条边的A 中点，FI的长度是IE的两倍，问阴影部分的面积为多 少？（ ）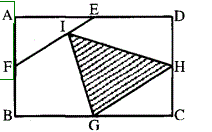



    答案：B
    解析：
    这个题目需要做辅助线，连接FG、EH。
    因为E、F、G、H分别为四条边的中点，则平行四边形EFGH的面积是矩形ABCD面积的 1/2，而三角形IGH的面积是平行四边EFGH面积的1/2，所以阴影部分的面积为1/4。

  • 第17题：

    在边长为1的正方形ABCD中，AC与BD相交于O，以A、B、C、D分别为圆心，以对角线长的一半为半径画圆弧与正方形的边相交，如图，则图中阴影部分的面积为多少?(π=3．14)


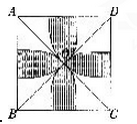    A.0．43
    B.0．57
    C.0．64
    D.0．71

    答案：C
    解析：

  • 第18题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )
    A. 11.75 B. 16.45 C. 19.625 D. 39. 25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10x10x2，所以大半圆的面积是1/2x1/4xπx10x10x2=25π（平方厘米）；
    小半圆的面积是π/2X5X5 = 12. 5π（平方厘米）；
    阴影的面积是25π-12. 5π=12. 5π=39. 25（平方厘米）。
    故本题选D。

  • 第19题：

    如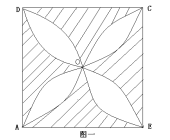，四边形ABCD是边长为1的正方形，弧AOB，BOC，COD，DOA均为半圆，则阴影部分的面积为



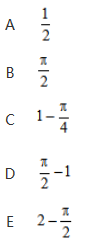    答案：E
    解析：

  • 第20题：

    如图6-15所示,正方形ABCD的对角线∣AC∣=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,则阴影部分的面积为（ ）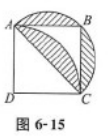

    A.π-1
    B.π-2
    C.π+1
    D.π+2
    E.π

    答案：B
    解析：

  • 第21题：

    在右图的长方形中，长和宽分别是6cm和4cm，阴影部分的面积和是10cm2，求四边形ABCD的面积为多少平方厘米？（ ）
    A. 2 B. 4
    C. 5 D. 8


    答案：B
    解析：
    SΔAGF=4X6/2=12(cm2)，它与阴影部分的面积和是12 + 10 = 22(cm2)，而五边形HCEFG的面积是长方形HEFG的3/4，即4X6x3/4 = 18(cm2)，所以四边形ABCD的面积是22 - 18 =4 (cm2)。

  • 第22题：

    如图8，四边形ABCD内接于⊙O，若∠BCD=130o，则∠BOD=_______°。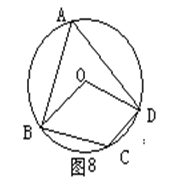


    答案：
    解析：
    100

  • 第23题：

    底面是边长为2的正三角形的三棱锥的主视图和俯视图如图所示，则其侧视图的面积为( )。


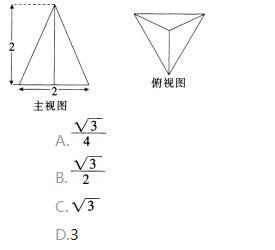    答案：C
    解析：

相关内容