itgle.com

某单位组织职工去进行义务劳动，第一天共有200人参加，以后每天都减少5人，经过11天，完成了所有劳动任务。假设每位职工的工作效率相等，若所有劳动任务要在7天完成，且每天参加的人数比前一天要多5人，问最后一天安排多少人？( )A.260 B.275 C.290 D.305

题目
某单位组织职工去进行义务劳动，第一天共有200人参加，以后每天都减少5人，经过11天，完成了所有劳动任务。假设每位职工的工作效率相等，若所有劳动任务要在7天完成，且每天参加的人数比前一天要多5人，问最后一天安排多少人？( )

A.260
B.275
C.290
D.305
相似考题

1.哺乳期女职工的哺乳时间( )。A、用人单位应在每天的劳动时间内为哺乳期女职工安排半小时哺乳时间B、用人单位应在每天的劳动时间内为哺乳期女职工安排1小时哺乳时间C、女职工生育多胞胎的，每多哺乳一个婴儿每天应增加半小时哺乳时间D、女职工生育多胞胎的，每多哺乳一个婴儿每天应增加40分钟哺乳时间

2.某工会为丰富职工生活，组织77名职工参加6项业余活动，所有职工都参加了，且由于活 动时间相同，每个职工只能参加一项活动。如果每项活动参加的人数不同，问参加人数最多的活动至少有多少人参加？（ ） A. 12 B. 13 C. 15 D. 16

3.某单位有80名职工参加了义务劳动、希望工程捐款和探望敬老院三项公益活动中的至少一项。只参加一项的人数与参加超过一项的人数相同，参加所有三项公益活动的与只捐款的人数均为12人，且只探望敬老院的人比只参加义务劳动的人多16人。问探望敬老院的人最多比参加义务劳动的人多多少人？A.28 B.32 C.36 D.44

4.若干人完成了植树2013棵的任务，每人植树的棵数相同。如果有5人不参加植树， 其余的人每人多植2棵不能完成任务，而每人多植3棵可以超额完成任务。问： 共有多少人参加了植树?A: 11 B: 33 C: 61 D: 183

更多“某单位组织职工去进行义务劳动，第一天共有200人参加，以后每天都减少5人，经过11天，完成了所有劳动任务。假设每位职工的工作效率相等，若所有劳动任务要在7天完成，且每天参加的人数比前一天要多5人，问最后一天安排多少人？( )”相关问题

  • 第1题：

    甲、乙两个单位分别有60和42名职工，共同成立A、B两个业余活动小组，所有职工每人至少参加1个。乙单位职工中仅参加A组的人数是只参加一个小组人数的60%，乙单位职工中参加B组的人数与参加A组的人数之比为3∶4，参加B组的人中，甲单位职工占5/8。问有多少人仅参加A组?

    A.35
    B.42
    C.46
    D.56

    答案：C
    解析：
    第一步，本题考查容斥问题。
    第二步，设乙单位只参加一个小组的人数为5x，则只参加A组的有5x·60%=3x名职工，那么只参加B组的有5x－3x=2x名职工，设乙单位AB组都参加的有y人。可列方程：（2x＋y）∶（3x＋y）＝3∶4，解得x＝y，那么乙单位中参加B组的有3x人，参加A组的有4x人，AB都参加的有x人，可列方程：3x＋4x－x＝42，解得x＝7，那么参加B组的有21人，只参加A组的有21人。

    那么甲单位只参加A组的有60－35＝25（人），那么两个单位只参加A组的有21＋25＝46（人）。

  • 第2题：

    某机关举行职工秋季田径运动会。已知：所有报名参加短跑比赛的职工都报名参加铅球比赛，所有报名参加跳远比赛的职工都没有报名参加铅球比赛，报名参加跳高比赛的职工也都报名参加了跳远比赛，而没有报名参加跳高比赛的职工也没有报名参加长跑比赛。
    根据以上陈述，可以得出以下哪项？

    A.有的报名参加铅球比赛的职工没有报名参加短跑比赛
    B.有的报名参加跳高比赛的职工没有参加长跑比赛
    C.所有报名参加跳远比赛的职工都报名参加长跑比赛
    D.所有报名参加短跑比赛的职工都没有报名参加长跑比赛

    答案：D
    解析：
    第一步，确定题型。
    根据题干关键词“所有”，确定为集合推理。
    第二步，翻译题干。
    ①所有报名短跑的都报名了铅球（短跑→铅球）；
    ②所有报名跳远的都没有报名铅球（跳远→?铅球）；
    ③所有报名跳高的都报名了跳远（跳高→跳远）；
    ④所有没有报名跳高的都没有报名长跑（?跳高→?长跑）。
    第三步，进行推理。
    A项：将①进行换位推理可得“有的报名铅球的报名了短跑”，根据“有的是”无法必然推出“有的不是”，该项无法推出；
    B项：将④进行逆否可得：所有报名长跑的都报名了跳高，再将其进行换位推理可得“有的报名跳高的报名了长跑”，根据“有的是”无法必然推出“有的不是”，该项无法推出；
    C项：将④进行逆否可得：长跑→跳远，“所有报名跳远”是对其“肯后”，根据肯后推不出必然结论，该项无法推出；
    D项：将①②③④进行递推可得：短跑→?长跑，即“所有报名短跑的都没有报名长跑”，该项可以推出。
    因此，选择D选项。

  • 第3题：

    某单位组织职工去进行义务劳动，第一天共有200人参加，以后每天都减少5人，经过11天，完成了所有劳动任务。假设每位职工的工作效率相等，若所有劳动任务要在1天完成， 且每天参加的人数比前一天要多5人，问最后一天安排多少人？

    A. 260
    B. 275
    C. 290
    D. 305

    答案：C
    解析：
    第一天200人，每天减少5人，第11天有200-5x(11-1)=150人，所有劳动任务需要 (200+150)x11÷2=1925人次。现在需要7天完成,则最中间一天即第4天安排了 1925÷7=275人，则最后一天安 排 275+(7-4)x5=290 人。

  • 第4题：

    某单位利用业余时间举行了3次义务劳动，总计有112人次参加，在参加义务劳动的人中，只参加1次，参加2次和3次全部参加的人数之比为5：4：1，问该单位共有多少人参加了义务劳动？（）

    • A、70 
    • B、72 
    • C、77 
    • D、80 
    • E、85 
    • F、92

    正确答案:A

  • 第5题：

    某单位利用业余时间组织了3次义务劳动，总计有112人次参加。在参加义务劳动的人中，只参加1次、参加2次和3次全部参加的人数之比为5:4:1.问该单位共有多少人参加了义务劳动?

    • A、70 
    • B、80 
    • C、85 
    • D、102

    正确答案:A

  • 第6题：

    某单位利用多余时间举行了3次义务劳动，总计有112人次参加。在参加义务劳动的人中，只参加1次，参加2次和3次全部参加的人数之比为5:4:1。问该单位共有多少人参加了义务劳动? A.70 B.80 C.85 D.102

    • A、70 
    • B、80 
    • C、85 
    • D、102

    正确答案:A

  • 第7题：

    单选题
    工厂组织职工参加周末公益劳动，有 80%的职工报名参加。其中报名参加周六活动的人数与报名参加周日活动的人数比为2︰1，两天的活动都报名参加的人数为只报名参加周日活动的人数的 50%。问未报名参加活动的人数是只报名参加周六活动的人数的：
    A

    20%

    B

    30%

    C

    40%

    D

    50%


    正确答案： A
    解析：

  • 第8题：

    某工会为丰富职工生活，组织77名职工参加6项业余活动，所有职工都参加了，且由于活 动时间相同，每个职工只能参加一项活动。如果每项活动参加的人数不同，问参加人数最 多的活动至少有多少人参加？（ ）


    A. 12
    B. 13
    C. 15
    D. 16

    答案：D
    解析：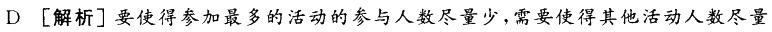

  • 第9题：

    某部队组织新兵从甲地到乙地进行长途拉练。去的时候第一天走25公里，以后每天都比前一天多走5公里，结果最后一天只走25公里便到达了目的地。回程时，第一天走35公里，以后还是每天比前一天多走5公里，结果最后一天只走30公里便回到出发地。则甲乙两地相距（ ）公里。

    A175
    B200
    C225
    D250


    答案：B
    解析：

  • 第10题：

    用人单位应当在每天的劳动时间内为哺乳期女职工安排（）小时哺乳时间；女职工生育多胞胎的，每多哺乳1个婴儿每天增加（ ）小时哺乳时间。职工，用人单位不得延长劳动时间或者安排夜班劳动。

    • A、2，1
    • B、1，1
    • C、1，0.5

    正确答案:B

  • 第11题：

    某单位利用业余时间举行了3次义务劳动，总计有112人次参加。在参加义务劳动的人中，只参加1次、参加2次和3次全部参加的人数之比为5:4:1.问该单位共有多少人参加了义务劳动？（）

    • A、70 
    • B、80 
    • C、85 
    • D、102

    正确答案:A

  • 第12题：

    某单位利用业余时间举行了3次义务劳动，总计有112人次参加。在参加义务劳动的人中，只参加1次，参加2次和3次全部都参加的人数之比为5：4：1。问该单位共有多少人参加了义务劳动？（）

    • A、70 
    • B、80 
    • C、85 
    • D、102

    正确答案:A

  • 第13题：

    单选题
    某单位利用业余时间举行了3次义务劳动，总计有128人次参加。在参加义务劳动的人中，只参加1次、参加2次和3次全部参加的人数之比为5:4:1。则该单位共有多少人参加了义务劳动？（　　）
    A

    70

    B

    80

    C

    85

    D

    102


    正确答案： A
    解析：
    根据参加人数之比，可以设参加1次劳动的人数为5x，参加2次的人数为4x，参加3次的人数为x，因为总计有128人次参加，则有5x＋2×4x＋3×x＝128，解得x＝8，则该单位共有（5＋4＋1）×8＝80人参加了义务劳动。故本题选B。

  • 第14题：

    单选题
    某单位安排职工参加百分制业务知识考试，小周考了88分，还有别外2人的得分比他低。若所有人的得分都是整数，没有人得满分，且任意5人的得分不完全相同，问参加考试的最多有多少人？（）
    A

    38

    B

    44

    C

    50

    D

    62


    正确答案： B
    解析： 全站数据：本题共被作答1次，正确率为0.00%，易错项为B解析为了让参加考试的人”最多”，则尽可能在每一个分数段都有尽可能多的人分数相同。从88分-99分，共有12个整数分数可以重复，同时又由于”任意5人的得分不完全相同”，所以要求重复的分数的人数最多为4人。这样一共有48人，再加上两个低于88分的人，所以最多50人。故正确答案为C。速解本题与”抽屉原理”的反客为主思想完全相同，逆向思维简化思维量。

相关内容