长方形ABCD的面积是72平方厘米,E、F分别是CD、BC的中点,三角形AEF的面积是()平方厘米。A 24 B 27 C 36 D 40
题目
长方形ABCD的面积是72平方厘米,E、F分别是CD、BC的中点,三角形AEF的面积是()平方厘米。
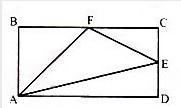

A 24
B 27
C 36
D 40
B 27
C 36
D 40
相似考题
更多“长方形ABCD的面积是72平方厘米,E、F分别是CD、BC的中点,三角形AEF的面积是()平方厘米。 ”相关问题
-
第1题:
如下图,正方形ABCD边长为10厘米,一只小蚂蚁E从A点出发均速移动,沿边AB、BC、CD前往D点。问哪个图形反映了三角形AED的面积与小蚂蚁行走时间的关系?
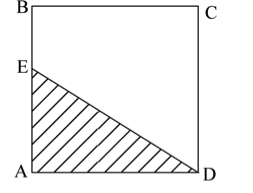
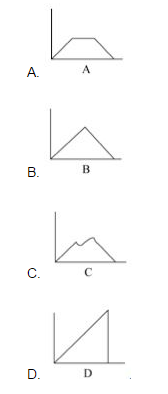 答案:A解析:此题考查三角形AED的面积计算变化情况,根据点E的运动,由A→B的运动过程中,三角形AED的底边不变,高变大,面积变大;由B→C的运动过程中,底边不变,高也不变,所以面积不变;由C→D的运动过程中,底边不变,高变小,面积变小。所以面积的变化为先变大,中间不变,后边小。正确答案为A。
答案:A解析:此题考查三角形AED的面积计算变化情况,根据点E的运动,由A→B的运动过程中,三角形AED的底边不变,高变大,面积变大;由B→C的运动过程中,底边不变,高也不变,所以面积不变;由C→D的运动过程中,底边不变,高变小,面积变小。所以面积的变化为先变大,中间不变,后边小。正确答案为A。 -
第2题:
如图所示,长方形恰好分为六个正方形,其中最小的正方形面积为1平方厘米,则这个长方形的面积是: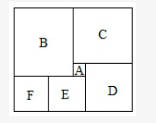 A.143平方厘米
A.143平方厘米
B.132平方厘米
C.110平方厘米
D.90平方厘米答案:A解析:第一步,本题考查几何问题,属于平面几何类。
第二步,设正方形E、F的边长为x厘米,则B正方形边长为(2x-1)厘米,D正方形边长为(x+1)厘米,C正方形边长为(x+2)厘米。
第二步,根据宽相等可以建立等式(2x-1)+x=(x+2)+(x+1),解得x=4。
第三步,宽为(2x-1)+x=11(厘米),长为2x-1+x+2=13(厘米)。面积为11×13=143(平方厘米)。 -
第3题:
长方形ABCD的面积是72平方厘米,E、F分别是CD,BC的中点。问三角形的面积为多少平方厘米?A.24
B.27
C.36
D.40 答案:B解析:
答案:B解析:
-
第4题:
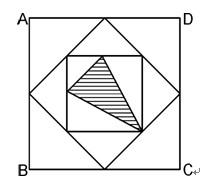
下图中的大正方形ABCD的面积是1平方厘米,其他点都是它所在边的中点。那么,阴影三角形的面积是多少平方厘米?()
 A. 5/28
A. 5/28
B. 7/34
C. 3/32
D. 5/38答案:C解析:[解析] 阴影三角形面积为最小正方形的3/8,最小正方形面积为第二大正方形面积的1/2,第二大正方形面积是最大正方形的1/2,则阴影三角形的面积为3/8×1/2×1/2=3/32(厘米2)。故选C。 -
第5题:
右图是由5个相同的小长方形拼成的大长方形,大长方形的周长是88厘米,问大长方形的面积多少平方厘米?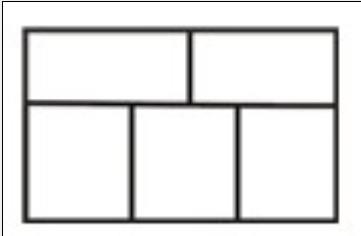 A. 472平方厘米
A. 472平方厘米
B. 476平方厘米
C. 480平方厘米
D. 484平方厘米答案:C解析:解题指导: 总面积应该为5的倍数,故答案为C。 -
第6题:
如下图所示,已知△ABC的面积为240平方厘米,D是BC的中点,AD的长是AE长的3倍,EF的长是BF长的3倍,那么,△AEF的面积是多少平方厘米?( )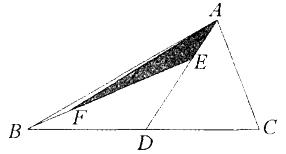 A. 27.5
A. 27.5
B. 40
C. 30
D. 25答案:C解析:若已知两个三角形的高相等,则二者面积之比等于底边之比。本题中D是BC的中点,故
-
第7题:
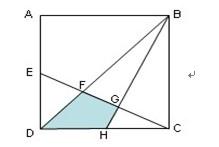
正方形ABCD的面积是120平方厘米,E、H分别是AD和DC的中点,求阴影部分的面积( )。
 A.14
A.14
B.16
C.17
D.18答案:A解析:
-
第8题:
长方形A BCD的面积是72平方厘米,E、F分别是CD、BC的中点。问三角形的面积为多少平方厘米?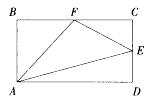 A.24
A.24
B.27
C.36
D.40答案:B解析: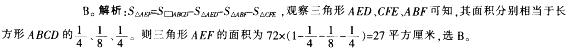
-
第9题:
如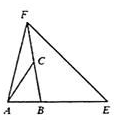 ,已知AE=3AB,BF=2BC。若ΔABC的面积是2,则ΔAEF的面积为A.14
,已知AE=3AB,BF=2BC。若ΔABC的面积是2,则ΔAEF的面积为A.14
B.12
C.10
D.8
E.6答案:B解析:因为是等高三角形,故面积比等于底边比.BF=2BC,.△ABF=2S△ABC=4 AE=3AB,.△AEF=3S△ABF=12故选B -
第10题:
图中的大正方形ABCD的面积是1平方厘米,其他点都是它所在边的中点。弧是一个内切于小正方形IJKL的半圆弧,PQ、OP是与弧半径相等的圆的四分之一圆弧,则阴影区的面积是多少平方厘米?( )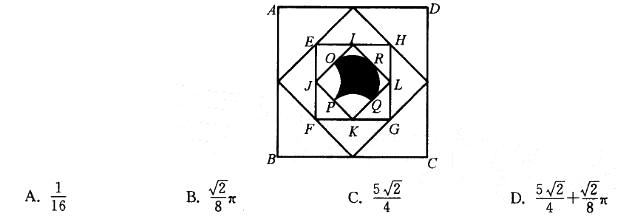 答案:A解析:由正方形是大正方形面积的1/4,小正方形IJKL是正方形EFHG面积的1/2,故小正方形IJKL是大正方形ABCD面积的1/8,如下图所示,图中的阴影部分面积是小正方形IJKL 的一半,所以阴影区的面积为大正方形面积的1/16。A为正确选项。
答案:A解析:由正方形是大正方形面积的1/4,小正方形IJKL是正方形EFHG面积的1/2,故小正方形IJKL是大正方形ABCD面积的1/8,如下图所示,图中的阴影部分面积是小正方形IJKL 的一半,所以阴影区的面积为大正方形面积的1/16。A为正确选项。
-
第11题:
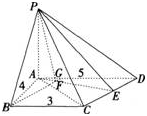
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。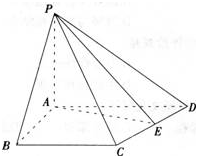 答案:解析:
答案:解析:
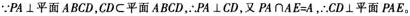

-
第12题:
单选题长方形的长是1.25分米,宽是8厘米,面积是()平方厘米。A10
B100
C1000
正确答案: C解析: 暂无解析 -
第13题:
如右图,在梯形ABCD中,点E、F分别是腰AB、CD上的点.
(1)证明:如果E、F为中点时,有 EF=1/2(AD+BC);
(2)请写出(1)中命题的逆命题,并判断该逆命题是否成立,若成立,请给予证明;若不成立,请说明理由.
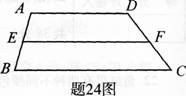 答案:解析:(1)证明:连接AC,设AC中点为日,连接EH、FH
答案:解析:(1)证明:连接AC,设AC中点为日,连接EH、FH

逆命题不成立.
理由如下:连接AC,连接BD,延长AD至M使DM=AD,延长BC至N,使CN=AD,连接MN、DN.由DM平行且等于CN可知,DN平行且等于AC由ADBN可知,BD+DM>BN,即BD+AC>BC+AD
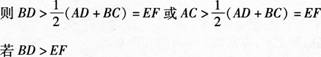
又AD<EF可知AD<EF<BD过点D作直线交AB于Q,则AD<DQ<BD,其中必有DQ=EF同理,若AC>EF,Q为DC上-点,则必有AQ=EF且A、D均不是AB、CD的中点故命题错误. -
第14题:
如图,在长方形ABCD中,已知三角形ABE、三角形ADF与四边形AECF的面积相等,则三角形AEF与三角形CEF的面积之比是
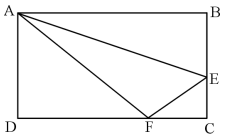 A.5∶1
A.5∶1
B.5∶2
C.5∶3
D.2∶1答案:A解析:第一步,三角形ABE、三角形ADF与四边形AECF的面积相等,则三者各占长方形ABCD面积的1/3。连接辅助线AC,则三角形ACD的面积为长方形的1/2。?
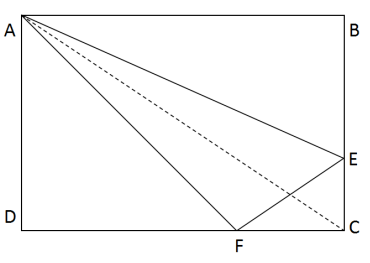
第二步,三角形ADF与三角形ACD的高相同,都为AD,三角形高相同,底边之比等于面积之比,则FD:CD=2:3,所以CF=1/3CD,同理CE=1/3BC,因此三角形CEF的面积为长方形面积的1/18,则三角形AEF的面积为长方形面积的1/3-1/18=5/18,所以两者面积之比为5:1。解法二:赋值长方形的长为6,宽为3,则长方形的面积为18。三角形ABE、三角形ADF与四边形AECF的面积相等,则三者的面积各为6。那么FD的长为4,CF长2,则CE的长为1,则三角形CEF的面积为1,三角AEF的面积为6-1=5,则两者的面积之比为5:1。因此,选择A选项。 -
第15题:
如图所示,矩形ABCD的面积为1,E、F、G、H分别为四条边的中点,FI的长度是IE的两倍,问阴影部分的面积为多少?

 答案:B解析:解题指导: 作辅助线。连接FG、EH。那么平行四边形EFGH的面积为矩形ABCD的一半,三角形GIH的面积又是平行四边形EFGH面积的一半,所以因应面积为1/4。故答案为B。
答案:B解析:解题指导: 作辅助线。连接FG、EH。那么平行四边形EFGH的面积为矩形ABCD的一半,三角形GIH的面积又是平行四边形EFGH面积的一半,所以因应面积为1/4。故答案为B。 -
第16题:
如图所示,矩形ABCD的面积为1,E、F、G、H分别为四条边的A 中点,FI的长度是IE的两倍,问阴影部分的面积为多 少?( )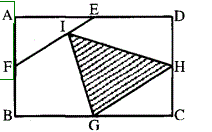
 答案:B解析:这个题目需要做辅助线,连接FG、EH。
答案:B解析:这个题目需要做辅助线,连接FG、EH。
因为E、F、G、H分别为四条边的中点,则平行四边形EFGH的面积是矩形ABCD面积的 1/2,而三角形IGH的面积是平行四边EFGH面积的1/2,所以阴影部分的面积为1/4。 -
第17题:
在右图的长方形中,长和宽分别是6cm和4cm,阴影部分的面积和是 IOcm2,四边形ABCD的面积为( )平方厘米。
A. 2 B. 4C. 5 D. 8答案:B解析:SAAGF = 4X6 + 2 = 12(cm2),它与阴影部分的面积和是 12 + 10 = 22(cm2),而五达形HCEFG的面积是长方形HEFG的等于4X6x "=18(cm2),所以四边形ABCD 的面积是 22 — 18 = 4(cm2)。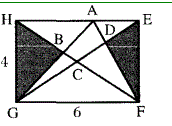
-
第18题:
一个长方形的长与宽的比是14:5,如果长减少l3厘米,宽增加l3厘米,则面积增加182平方厘米,那么原长方形面积是多少平方厘米?A.448
B.630
C.812
D.1120答案:B解析:设原长方形的长为l4a,宽为5a,由题意可得,(14a一l3)x(5a+13)=14a×5a+182,解得a=3,
原长方形面积是14×3×5×3=630平方厘米,应选择8。 -
第19题:
将一块长10厘米、宽4厘米的长方形平板切割成A、B、C共3块,其中C块的面积为22平方厘米,B为等腰三角形,那么A块的面积是( )。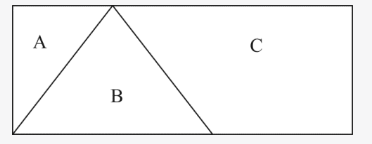 A.6平方厘米
A.6平方厘米
B.12平方厘米
C.8平方厘米
D.4平方厘米答案:A解析:第一步,本题考查几何问题,属于平面几何的面积计算问题。
第二步,长方形的长为10厘米,宽为4厘米,那么该矩形的面积为10×4=40(平方厘米),C的面积为22平方厘米,那么A+B的面积为40-22=18(平方厘米)。做三角形B的垂线,如图所示,B为等腰三角形,则三线合一,那么可得三角形A的面积为三角形B的面积的一半,则△B的面积=2×△A的面积。那么△A的面积为18÷3=6(平方厘米)。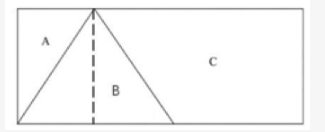
-
第20题:
如图6-11所示,在长方形ABCD中,三角形AOB是直角三角形且面积为54,OD=16,那么长方形ABCD的面积为( )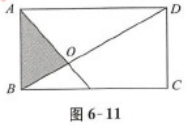 A.150
A.150
B.200
C.300
D.340
E.380答案:C解析: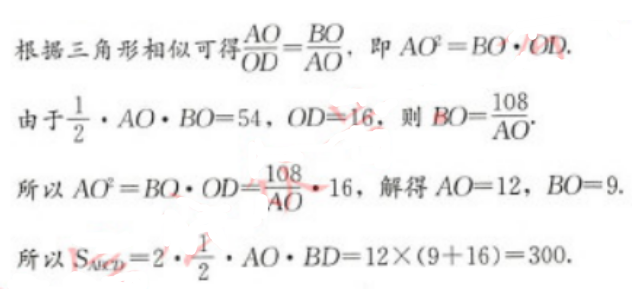
-
第21题:
在右图的长方形中,长和宽分别是6cm和4cm,阴影部分的面积和是10cm2,求四边形ABCD的面积为多少平方厘米?( )
A. 2 B. 4
C. 5 D. 8答案:B解析:SΔAGF=4X6/2=12(cm2),它与阴影部分的面积和是12 + 10 = 22(cm2),而五边形HCEFG的面积是长方形HEFG的3/4,即4X6x3/4 = 18(cm2),所以四边形ABCD的面积是22 - 18 =4 (cm2)。 -
第22题:
如图,平行四边形ABCD的面积是54平方厘米,点E、F、G分别是平行四边形ABCD边上的中点,H为AD边上的任意一点,则阴影部分的面积为( )平方厘米。
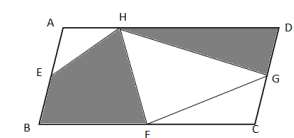 A. 27
A. 27
B. 28
C. 32
D. 36答案:A解析:方法一:如图所示,由于H为AD边上的任意一点,假设H点与A点重叠,则左边阴影为三角形ABF,其面积为三角形ABC的一半;右边阴影为三角形ADG,其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半,平行四边形ABCD的面积是54平方厘米,则阴影部分面积为27平方厘米。因此,本题答案为A选项。
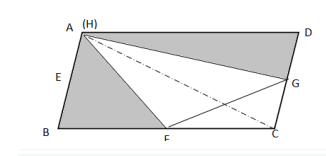
方法二:如图所示,连接BH和CH,由于点E、F、G分别是平行四边形ABCD边上的中点,则三角形AEH和BEH相等,三角形BFH和CFH相等,三角形CGH和DGH相等,因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米,则阴影部分面积为27平方厘米。因此,本题答案为A选项。
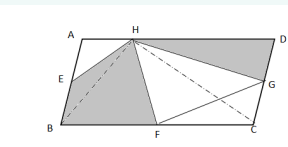
-
第23题:
长方形的长是1.25分米,宽是8厘米,面积是()平方厘米。
- A、10
- B、100
- C、1000
正确答案:B
