itgle.com

有62名学生，会击剑的有11人，会游泳的有56人，两种都不会用的有4人，问两种都会的学生有多少人? A. 1 人 B. 5 人 C. 7 人 D. 9 人

题目
有62名学生，会击剑的有11人，会游泳的有56人，两种都不会用的有4人，问两种都会的学生有多少人?

A. 1 人
B. 5 人
C. 7 人
D. 9 人
相似考题

1.有一个老年活动中心，会下象棋的偶59人，会下围棋的有48人，两种棋都不会下的有12人，两种棋都会下的有30人，问这个俱乐部一共有多少人?A.89人 B.107人 C.129人 D.137人

2.某俱乐部会下中国象棋的有85人，会下围棋的有78人，两种都会下的有35人，两种都不会下的有18人，那么该俱乐部共有多少人?A．128B．146C．158D．166

3.某单位有青年员工85人，其中68人会骑自行车，62人会游泳，既不会骑车又不会游泳的有12人，则既会骑车又会游泳的有多少人?（　　）A.57B.73C.130D.69

4.某班共有学生60人，其中有40人会游泳，45人会骑自行车，48人会打乒乓球，这三项运动都会的学生有22人，问这个班级最多有多少学生这三项运动都不会?（ ） A．4 B．6 C．7 D．11

参考答案和解析
答案：D
解析：
会游泳的有56人，则不会游泳的只有6人，两种都不会的只有4人，那么不会游泳的6人中有2个会击剑，那么都会的人数是11-2=9。故答案为D。
更多“有62名学生，会击剑的有11人，会游泳的有56人，两种都不会用的有4人，问两种都会的学生有多少人? ”相关问题

  • 第1题：

    有62 名学生，会击剑的有 11 人，会游泳的有 56 人，两种都不会的有 4人，问两种都会的学生有多少人？( )

    A.1 人

    B.5 人

    C.7 人

    D.9 人


    正确答案：D

  • 第2题：

    外语学校一年级有120人，其中：70人会英语，70人会德语，60人会法语，40人既会英语又会德语，30人既会英语又会法语，20人既会德语又会法语，15人英语、德语、法语三种语言都会。会且只会两种语言的有多少人?（ ）

    A．40

    B．45

    C．50

    D．60


    正确答案：B

    如图，只会两种语言的人是涂黑部分。
    15人英语、德语、法语三种语言都会， 
    因为40人既会英语又会德语，所以25人只会说英语和德语；
    因为30人既会英语又会法语，所以15人只会说英语和法语；
    因为20人既会德语又会法语，所以5人只会说德语和法语，
    综上，会且只会说两种语言的人数共有25+15十5＝45人。故应选B。

  • 第3题：

    某班在筹备联欢会时发现很多同学都会唱歌和乐器演奏，但有部分同学这2种才艺都不会。具体有4种情况：只会唱歌，只会乐器演奏，唱歌和乐器演奏都会，唱歌和乐器演奏都不会。现知会唱歌的有22人，会乐器演奏的有15人，两种都会的人数是两种都不会的5倍。这个班至多有（ ）人。

    A.27
    B.30
    C.33
    D.36

    答案：C
    解析：
    第一步，本题考查容斥问题，属于二集合容斥类。
    第二步，设该班共有x人，唱歌和乐器演奏都不会的有y人，则两种都会的有5y人，根据二集合容斥公式可得：x－y＝22＋15－5y，化简得：x＝37－4y。
    第三步，要使x最大，则y应最小，当y＝1时，x＝33，故这个班至多有33人。

  • 第4题：

    某研究室有12人，其中：7人会英语，7人会德语，6人会法语，4人既会英语又会德语，3人既会英语又会法语，2人既会德语又会法语，1人英语、德语、法语三种语言都会。会且只会两种语言的有多少人
    A．8 B．4 C．5 D．6


    答案：D
    解析：
    这是容斥问题，会且只会两种语言的有：
    A∩B＋B∩C＋C∩A－3A∩B∩C=4+3+2-3=6人。

  • 第5题：

    某单位有青年员工85人，其中68人会骑自行车，62人会游泳，既不会骑车又不会游泳的有12人，则既会骑车又会游泳的有多少人?( )

    A. 57人
    B. 73人
    C. 130人
    D. 69人

    答案：A
    解析：
    用集合法68+62+12-85=57。故答案为A。

  • 第6题：

    50名学生做物理、化学两种实验，已知物理实验做的正确的有40人，化学实验做的正确的有31人，两种实验都做错的有4人，那么这两种实验都做对的有多少人？


    正确答案: 25

  • 第7题：

    某单位有青年员工85人，其中68人会骑自行车，62人会游泳，既不会骑车又不会游泳的有12人，则既会骑车又会游泳的有多少人( )

    • A、57人
    • B、73人
    • C、130人
    • D、69人

    正确答案:A

  • 第8题：

    一个俱乐部，会下象棋的有 69 人，会下围棋的有 58 人，两种棋都不会下的有 12人，

    两种棋都会下的有 30 人，问这个俱乐部一共有多少人？( )

    A.109 人

    B.115 人

    C.127 人

    D.139 人


    正确答案：A

  • 第9题：

    一个班里有30名学生，有12人会跳拉丁舞，有8人会跳肚皮舞，有10人会跳芭蕾舞。问 至多有几人会跳两种舞蹈？（ ）

    A. 12 人
    B. 14 人
    C. 15 人
    D. 16 人

    答案：C
    解析：
    根据三集合容斥原理公式：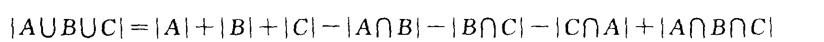

    要求会跳两种舞蹈的人最多，则需要让所有会跳舞的人都会两种舞蹈，此时会跳两种舞蹈的人数为（12 + 8 + 10)÷2=15(人）。具体构造如下：会跳拉丁的12人中有7人会拉丁和芭蕾，5人会拉丁和肚皮，这时有12 人会跳两种舞蹈；剩下的3个人都会芭蕾和肚皮两种舞蹈，此时共有12 + 3 = 15(人）会两种舞蹈。

  • 第10题：

    某班56名学生参加了奥数或作文课外兴趣小组的活动，其中参加奥数的有32人，参加作文的有35人，问两种活动都参加的有多少人?()

    A. 3
    B. 11
    C. 21
    D. 24

    答案：B
    解析：
    两种活动都参加得人有32+35-56=11人。故答案为B。

  • 第11题：

    有 62 名学生，会击剑的有 11 人，会游泳的有 56 人，两种都不会用的有 4 人，问两种都 会的学生有多少人?
    A．1 人 B。5 人 C、7 人 D. 9 人


    答案：D
    解析：
    此题简单，直接可列式求结果，即56＋11－（62－4）＝9人。故选D。

  • 第12题：

    某高校对一些学生进行问卷调查。在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试参加的有46人，不参加其中任何一种考试的有15人。问接受调查的学生共有多少人（）

    • A、120
    • B、144
    • C、177
    • D、192

    正确答案:A

  • 第13题：

    88名学生参加运动会，参加游泳比赛的有23人，参加田径比赛的有33人，参加球类比赛的有54人，既参加游泳比赛又参加田径比赛的有5人，既参加田径比赛又参加球类比赛的有16人。已知每名学生最多可参加两项比赛，问只参加田径比赛的有多少人（）

    • A、20
    • B、17
    • C、15
    • D、12

    正确答案:D

  • 第14题：

    单选题
    某俱乐部会下中国象棋的有85人，会下围棋的有78人，两种都会下的有35人，两种都不会下的有18人，那么该俱乐部一共有多少人？（　　）
    A

    128

    B

    146

    C

    158

    D

    166


    正确答案： B
    解析：
    由容斥原理公式可知，该俱乐部会下围棋和象棋的人数为|A∪B|＝|A|＋|B|－|A∩B|＝85＋78－35＝128人，则该俱乐部一共有128＋18＝146人。

相关内容