itgle.com

甲、乙、丙三人沿圆形跑道跑步，同时从跑道某一固定点出发，甲按顺时针方向行走，乙与丙按逆时针方向行走，甲第一次遇到乙2分钟后遇到丙，再过8分钟第二次遇到乙。已知乙的速度是甲的2/3，圆形跑道的周长为600米，则丙的速度为( )。 A. 14米/分 B. 15米/分 C. 16米/分 D. 17米/分

题目
甲、乙、丙三人沿圆形跑道跑步，同时从跑道某一固定点出发，甲按顺时针方向行走，乙与丙按逆时针方向行走，甲第一次遇到乙2分钟后遇到丙，再过8分钟第二次遇到乙。已知乙的速度是甲的2/3，圆形跑道的周长为600米，则丙的速度为( )。

A. 14米/分
B. 15米/分
C. 16米/分
D. 17米/分
相似考题

1.甲、乙两人沿直线从A地步行至B地，丙从B地步行至A地。已知甲、乙、丙三人同时出发，甲和丙相遇后5分钟，乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问AB两地的距离为多少米?

2.甲乙丙三人沿湖边散步，同时从湖边一固定点出发。甲按顺时针方向行走，乙和丙按逆时针方向行走，甲第一次遇到乙后1.25分钟遇到丙，再过3.75分钟第二次遇到乙。已知乙的速度是甲的，湖的周长是600米，则丙的速度为（ ）米/分。A. 24 B. 25 C. 26 D. 27

3.甲、乙、丙三人沿着400米环形跑道进行800米跑比赛，当甲跑1圈时，乙比甲多跑1/7圈。丙比甲少跑1/7圈。如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面（ ）

4.甲、乙、丙三人，甲每分钟走 50 米，乙每分钟走 40 米，丙每分钟走 35米，甲、乙从A 地，丙从 B 地同时出发，相向而行，丙遇到甲 2 分钟后遇到乙，那么，A、B 两地相距多少米？( )A.250 米B.500 米C.750 米D.1275 米

更多“甲、乙、丙三人沿圆形跑道跑步，同时从跑道某一固定点出发，甲按顺时针方向行走，乙与丙按逆时针方向行走，甲第一次遇到乙2分钟后遇到丙，再过8分钟第二次遇到乙。已知乙的速度是甲的2/3，圆形跑道的周长为600米，则丙的速度为( )。 ”相关问题

  • 第1题：

    甲、乙两人在圆形跑道上，同时从某地出发沿相反方向跑步。甲的速度是乙的3倍，他们第一次与第二次相遇地点之间的较短的跑道长度是100m。那么，圆形跑道的周长是（ ）m。

    A. 200
    B. 300
    C. 400
    D. 500

    答案：C
    解析：
    第一次相遇后，两人仍是沿相反方向跑步，到第二次相遇时，两人跑步距离之和为圆形跑道的周长。此时，乙跑的距离为较短的跑道，为100米，则甲跑的距离为300米，圆形跑道的周长为100 + 300 = 400(米)。故选 C。

  • 第2题：

    如图，在长方形跑道上，甲、乙两人分别从A、C处同时出发，按顺时针方向沿跑道匀速奔跑。已知甲、乙两人的速度分别为5米/秒、4.5米/秒。则当甲第一次追上乙时，甲沿长方形跑道跑过的圈数是：


    A.4
    B.4.5
    C.5
    D.5.5

    答案：C
    解析：
    起跑时，甲、乙相距20+12=32米，甲每秒比乙多跑5-4.5=0.5米，故甲第一次追上乙需要32/0.5=64秒。跑道一圈为（20+12）x2=64米，故甲第一次追上乙时，甲跑了64x5/64=5圈。

  • 第3题：

    甲、乙二人绕着圆形操场跑道散步，甲顺时针走，乙逆时针走，两人在跑道A处同时出发，甲每分钟走90米，乙每分钟走60米，当甲、乙两人在跑道B处相遇时，乙加快了速度，甲在原地停留4分钟后保持原来的速度继续往前走，最后甲、乙二人仍在A处相遇。已知该操场的周长为1800米，那么相遇后，乙的速度变为每分钟（ ）米。

    A.70
    B.80
    C.90
    D.100

    答案：C
    解析：
    第一步，本题考查行程问题。
    第二步，甲、乙在B处相遇，根据S=（+）×t代入数据：1800=（90+60）×t，解得t=12（分钟），则甲走了90×12=1080米，乙走了60×12=720米。
    第三步，要回到A处：甲要再走720米，用时720÷90=8分钟，加上原地停留的4分钟，共用时8+4=12分钟，故乙加速后再走1080米也需用时12分钟，加速后的速度为每分钟1080÷12=90米。

  • 第4题：

    单选题
    甲、乙、丙三人从400米环形跑道上三个前后等距的起点出发（甲在最后、丙在最前），沿顺时针方向跑步，三人的速度分别为8米／秒、6米／秒、4米／秒。为了保证三人同时到达终点（甲的起点），乙、丙又分别比甲提前一段时间出发，已知丙比乙提前10秒出发。求三人起点的间距为多少米？
    A

    50

    B

    60

    C

    70

    D

    80


    正确答案： B
    解析：

  • 第5题：

    甲、乙、丙、丁四人同时同地出发，绕一椭圆形环湖栈道行走，甲顺时针行走，其余三人逆时针行走，已知乙的行走速度为60米/分钟,丙的速度为48米/分钟,甲在出发6、7、8分钟时分别与乙、丙、丁三人相遇，求丁的行走速度是多少

    A.31米/分钟
    B.36米/分钟
    C.39米/分钟
    D.42米/分钟

    答案：C
    解析：

  • 第6题：

    甲、乙、丙三人沿着环形操场跑步，乙与甲、丙的方向相反。甲每隔19分钟追上丙一次，乙每隔5分钟与丙相遇一次。如果甲与乙的速度比为5：4，那么甲的速度是丙的速度的多少倍?

    A.1．28
    B.1．6
    C. 2
    D.2.5

    答案：B
    解析：
    甲速度为5x乙速度为4x，丙速度为，'则甲追上丙一圈距离为l9(5x-y)，乙与丙相遇共同走一圈为5(4x+y)．19(5x—y)=5(4x+y)，

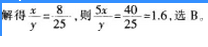
  • 第7题：

    单选题
    甲、乙、丙三人从400米环形跑道上三个前后等距事物起点出发（甲在最后、丙在最前）沿顺时针方向跑步，三人的速度分别为8米／秒、6米／秒、4米/秒。为了保证三人同时到达终点（甲的起点），乙、丙又分别比甲提前一段时间出发，已知丙比乙提前10秒出发。求三人起点的间距为多少米？
    A

    50

    B

    60

    C

    70

    D

    80


    正确答案： C
    解析：

  • 第8题：

    单选题
    甲、乙、丙、丁四人同时间地出发，绕一椭圆环形湖栈道行走，甲顺时针行走，其余三人逆时针行走，已知乙的行走速度为60米/分钟,丙的速度为48米/分钟,甲在出发6、7、8分钟时分别与乙、丙、丁三人相遇，求丁的行走速度是多少：
    A

    31米/分钟

    B

    36米/分钟

    C

    39米/分钟

    D

    42米/分钟


    正确答案： C
    解析：

相关内容