itgle.com

已知 x 为 1 个向量, 计算 x 以e为底的对数值的运算A．ln(x)B．log(x)C．Ln(x)D．log10(x)

题目

已知 x 为 1 个向量, 计算 x 以e为底的对数值的运算

A．ln(x)

B．log(x)

C．Ln(x)

D．log10(x)

相似考题

1.设总体X～N(μ，σ2)，X1，X2，X3，X4是正态总体X的一个样本，为样本均值，S2为样本方差，若μ为未知参数且σ为已知参数，下列随机变量中属于统计量的有( )。A．X1-X2+X3B．2X3-μC．D．E．

2.从均值为μ、方差为σ2的总体中抽得一个容量为n的样本x1,x2,…,xn,其中μ已知,σ2未知,下列________是统计量。A．x1+x2+x3B．min{x1,x2,…,xn}C．x1+x2-μD．(x1-2μ)/σ

3.若一个栈以向量V[1．．n]存储，且空栈的栈顶指针top为n+1，则将元素x入栈的正确操作是(37)。A．top=top+1；V[top]=x；B．V[top]=x；top=top+1；C．top=top-1；V[top]=x；D．V[top]=x；top=top-1；

4.从均值为μ方差为σp>2p>的总体中抽得一个容量为n的样本X1，X2，…，Xn，其中μ已知，σp>2p>未知，下列各项属于统计量的有( )。A．X1+X2+X3B．min{X1，X2，X3，…，Xn}C．X1+X2-μD．(X1-2μ)/σE．X1+X2+σ

参考答案和解析
B
更多“已知 x 为 1 个向量, 计算 x 以e为底的对数值的运算”相关问题

  • 第1题：

    假设X～N(5,9),已知标准正态分布函数值φ(0.5)=0.6915,为使P{X《a}0.6915,则常数a《6.5。()


    正确答案:对

  • 第2题：

    已知函数 y=x²-4x+3。

    （1）画出函数的图象；

    （2）观察图象，当x取哪些值时，函数值为0？

  • 第3题：

    下面的叙述中正确的是______。

    A．以80x86为CPU的PC机，在实地址工作方式下，其中断向量长度为8个字节

    B．以80x86为CPU的PC机，在实地址工作方式下，其中断向量长度为4个字节

    C．以80x86为CPU的PC机，在实地址工作方式下，其中断向量长度为2个字节

    D．以80x86为CPU的PC机，在实地址工作方式下，其中断向量长度为1个字节


    正确答案：B
    解析：在实地址模式下，中断向量表固定存放在00000H～003FFH内存区域内。在中断向量表中，每一个中断向量对应一个中断服务程序入口地址(段地址和偏移地址)，每个入口地址占4个字节。

  • 第4题：

    加权法求算术均数的公式中，∑Xf表示

    A.各变量值的和
    B.将各变量求和，有m个相同数值x时可计算xf，其中f=m
    C.∑Xf是直接法中∑X的精确计算，同时还可以简化运算
    D.∑Xf可理解为(∑X)f
    E.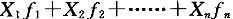，X为各组段的组中值，f表示各组频数

    答案：E
    解析：
    计算均数时，直接法的x代表变量值，加权法的x是组中值。

  • 第5题：

    已知向量a=(-3，1)，b=(x，9)，若a⊥b，则x=( )。

    A.1
    B.2
    C.3
    D.4

    答案：C
    解析：
    向量a=(x1，y1)与b=(x2，y2)垂直，则x1x2+y1y2=0，代入数值可得x=3，选择C。

  • 第6题：

    已知某一CODE39条码为：APWB5D2X1，请计算该条码的校验码X1。


    正确答案: 首先依据Code39条码的字符值分配表，写出每个字符代表的数值：    
     A    P    W    B    5    D    2
    ①：10   25   32    11   5    13   2
    ②：字符值的总和为98
    ③：②除以43，即98÷43＝2余12
    ④：③中的余数值12对应的Code39码的字符为C
    ⑤：因此可以得到该CODE39条码为：APWB5D2C

  • 第7题：

    已知x为一个向量，计算其反余弦函数的运算为（）。

    • A、COS（X）
    • B、aCOS（x）
    • C、cos（x）
    • D、acos（x）

    正确答案:D

  • 第8题：

    已知 X 和 Y，用变形补码计算 X+Y 和 X-Y，并指出运算结果是否溢出： X=-0.1101，Y=0.0110


    正确答案:方法一：（单符号位判溢）
    [X]补=10.0000-0.1101=1.0011（mod2）
    [Y]补=10.0000+0.0110=0.0110（mod2）
    [-Y]补=10.0000-0.0110=1.1010（mod2）
    [X+Y]补=[X]补+[Y]补=1.0011+0.0110=1.1001无溢出（负+正）
    [X-Y]补=[X]补+[-Y]补=1.0011+1.1010=0.1101有溢出（负-正）。负溢出
    方法二：（双符号位判溢）
    [X]补=100.0000-0.1101=11.0011（mod4）
    [Y]补=100.0000+0.0110=00.0110（mod4）
    [-Y]补=100.0000-0.0110=11.1010（mod4）
    [X+Y]补=[X]补+[Y]补=11.0011+00.0110=11.1001无溢出。双符号位11
    [X-Y]补=[X]补+[-Y]补=11.0011+11.1010=10.1101有溢出。双符号位10

  • 第9题：

    已知x，y为数值型数据，初值为0，下列语句中正确的赋值语句是（）。

    • A、x+y=30
    • B、10=x*y*y
    • C、y=x+30
    • D、3y=x

    正确答案:C

  • 第10题：

    已知中子的质量为1.67×10-27kg.假定一个中子沿x方向以2000ms-1的速度运动，速度的测量误差为0.01%，则中子位置的不确定量最小为（）（用不确定关系Δx·ΔPx≥h计算）。


    正确答案:3.16×10-7

  • 第11题：

    问答题
    设某客观现象可用X=（x1，x2，x3）′来描述，在因子分析时，从约相关阵出发计算出特征值为λ1=1.754，λ2=1，λ3=0.255，由于（λ1+λ2）/（λ1+λ2+λ3）≥85％，所以找前两个特征值所对应的公共因子即可，又知λ1，λ2对应的正则化特征向量分别为（0.707，-0.316，0.632）’及（0，0.899，0.4470）’，要求：计算第一公因子对X 的“贡献”。

    正确答案： 因为是从约相关阵计算的特征值，所以公共因子对X的“贡献”为g12=λ1=1.754.
    解析： 暂无解析

  • 第12题：

    问答题
    设A为n阶方阵，若对任意n维向量X=（x1，x2，…，xn）T都有AX=0.证明：A=0.

    正确答案：
    证明:由对任意n维向量X都有AX=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立.
    所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0.
    解析： 暂无解析

  • 第13题：

    已知x为一个向量,计算In(x)的MATLAB命令是计算()。

    A、Ln(x)

    B、log(x)

    C、lg10(x)

    D、In(x)


    参考答案：B

  • 第14题：

    加权法求算术均数的公式中；∑xf表示：

    A．各变量值的和

    B．将各变量求和，有m个相同数值χ时可计算xf，其中f＝m

    C．∑xf是直接法中∑x的精确计算，同时还可以简化运算

    D．∑xf可理解为(∑x) f

    E．x1f1＋x2f2＋…xufu，x为各组段的组中值，f表示各组频数


    正确答案：E

  • 第15题：

    设A是n阶矩阵,λ是A的特征值,其对应的特征向量为X,证明：λ^2是λ^3的特征值,X为特征向量,若A^2有特征值λ,其对应的特征向量为X,X是否一定为A的特征向量？说明理由.


    答案：
    解析：

  • 第16题：

    非负连续函数f(x)满足f(0)=0,f(1)=1.已知以曲线y=f(x)为曲边，以[0,x]为底的曲边梯形，其面积与f(x)的n+1次幂成正比，则f(x)的表达式为


    答案：
    解析：

  • 第17题：

    已知向量m=(sinx，cosx)，n=(cosx，cosx),f(x)=m*n，
    (1)求函数f(x)的最小正周期：
    (2)若f(x)≥1，求f(x)的取值范围。


    答案：
    解析：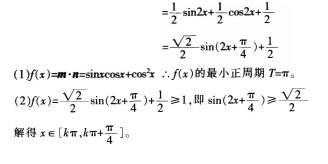

  • 第18题：

    零向量是指（）

    • A、向量X方向的值为0
    • B、向量的所有分量为0
    • C、向量的X，Y方向的值为0
    • D、向量Z方向的值为0

    正确答案:B

  • 第19题：

    已知x和y是两个等长的整数列表，那么表达式[i+jfori，jinzip（x，y）]的作用时计算这两个列表所表示的向量的和。


    正确答案:正确

  • 第20题：

    已知x和y是两个等长的整数列表，那么表达式sum（（i*jfori，jinzip（x，y）））的作用是计算这两个列表所表示的向量的内积。


    正确答案:正确

  • 第21题：

    若信息码字为11100011，生成多项式G（x）=x^5+x^4+x+1（^代表幂运算），则计算出的CRC校验码为（）

    • A、01101
    • B、11010
    • C、001101
    • D、011010

    正确答案:B

  • 第22题：

    单选题
    已知x为一个向量，计算其正弦函数的运算为（）。
    A

    SIN（X）

    B

    SIN（x）

    C

    sin（x）

    D

    sinx


    正确答案： B
    解析： 暂无解析

  • 第23题：

    问答题
    设A为n阶方阵，若对任意n维向量x(→)＝（x1，x2，…，xn）T都有Ax(→)＝0。证明：A＝0。

    正确答案：
    由对任意n维向量x(→)都有Ax(→)=0,知对基本单位向量组ε(→)1,ε(→)2,…,ε(→)n,Aε(→)i=0(i=1,2,…,n)成立。
    所以有A(ε(→)1,ε(→)2,…,ε(→)n)=0,即AE=0,故A=0。
    解析： 暂无解析

  • 第24题：

    判断题
    已知x和y是两个等长的整数列表，那么表达式sum（（i*jfori，jinzip（x，y）））的作用是计算这两个列表所表示的向量的内积。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容