itgle.com

已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定，求y(x)的极值.

题目
已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定，求y(x)的极值.

相似考题

1.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

2.(本题满分7分)设函数z=z(x，y)由方程x2+y2+z2=xyz确定，求δz/δy。

3.(本题满分8分) 设函数z=z(x，y)是由方程x+y3+z+e2x=1所确定的隐函数，求dz．

4.设函数y=y(x)由方程y+arcsinx=ex+y确定。求dy.

更多“已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定，求y(x)的极值. ”相关问题

  • 第1题：

    求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分．


    答案：
    解析：

  • 第2题：

    求函数(x，y)=x2+y2在条件2x+3y=1下的极值．


    答案：
    解析：
    解设F(x，y，λ)=X2+y2+λ(2x+3y-1)，

  • 第3题：

    设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．


    答案：
    解析：

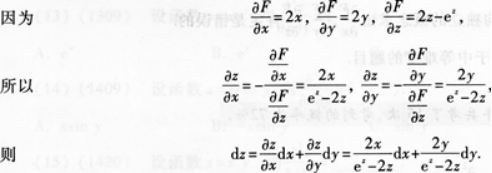
  • 第4题：

    求函数(x，y)=4(x-y)-x2-y2的极值．


    答案：
    解析：

    所以(2，-2)=8为极大值．

  • 第5题：

    设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.


    答案：
    解析：

  • 第6题：

    求函数f(x，y)=e2x(x+y2+2y)的极值.?


    答案：
    解析：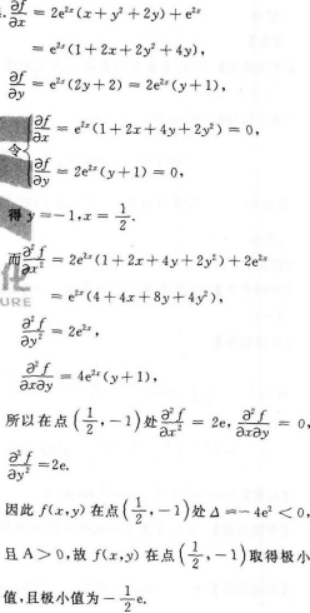

  • 第7题：

    填空题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

    正确答案： -1/7
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第8题：

    填空题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

    正确答案： 1
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第9题：

    填空题
    设函数y＝y（x）由方程y＝1－xey确定，则（dy/dx）|x＝0＝____。

    正确答案： -e
    解析：
    设F（x，y）＝y－1＋xey，则dy/dx＝－Fx′/Fy′＝－ey/（1＋xey）。x＝0时，y＝1，代入上式得（dy/dx）|x＝0＝－e。

  • 第10题：

    单选题
    已知函数y＝y（x）由方程ey＋6xy＋x2－1＝0所确定，则y″（0）＝（　　）。
    A

    －2

    B

    －1

    C

    0

    D

    1


    正确答案： D
    解析：
    ey＋6xy＋x2－1＝0两边对x求导，得ey·y′＋6xy′＋6y＋2x＝0①。两边再对x求导，得ey·y″＋ey（y′）2＋6xy″＋12y′＋2＝0②。当x＝0时，y＝0，将x＝0，y＝0代入①得y′（0）＝0，再将x＝y＝y′（0）＝0代入②得y″（0）＝－2。

  • 第11题：

    填空题
    设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝____。

    正确答案： (ln2-1)dx
    解析：
    2xy＝x＋y等式两边求微分，得2xyln2d（xy）＝dx＋dy，即2xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|x＝0＝（ln2－1）dx。

  • 第12题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    e


    正确答案： B
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第13题：

    求由方程2x2+y2+z2+2xy-2x-2y-4x+4=0确定的隐函数的全微分．


    答案：
    解析：
    所以dz=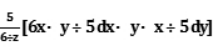

  • 第14题：

    设函数f(x，y)=X2+Y2+xy+3，求f(x，y)的极值点与极值．


    答案：
    解析：

  • 第15题：

    已知函数(x)=x4-4x+1．
    (1)求(x)的单调区间和极值；
    (2)求曲线y=(x)的凹凸区间．


    答案：
    解析：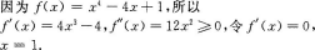

    列表如下，



    由表可知曲线(x)的单调递减区间为(-∞，1)，单调递增区间为(1，+∞)．由于"(x)=12x2≥0，所以为凹曲线，凹区间为(-∞，+∞)，极小值为(1)=1-4+1=-2．

  • 第16题：

    设z=z(x,y)是由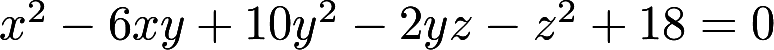 确定的函数，求 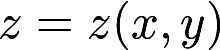的极值点和极值


    答案：
    解析：

  • 第17题：

    设函数y(x)是微分方程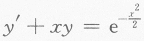满足条件y(0)=0的特解.
    　　(Ⅰ)求y(x)；
    　　(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.


    答案：
    解析：

  • 第18题：

    设Z=Z(x，Y)是由方程x+y3+z+e2=1确定的函数，求dz


    答案：
    解析：
    利用隐函数求偏导数公式，记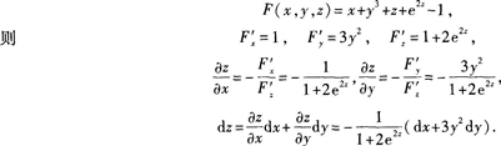

  • 第19题：

    问答题
    求由方程x2＋y2＋z2－xz－yz－2x－2y＋2z－6＝0确定的函数z＝z（x，y）的极值。

    正确答案：
    先求出函数z的各个偏导:
    由原方程可得,原方程两边对x求导得
    2x+2z·zx′-z-(x+y)zx′-2+2zx′=0①
    原方程两边对y求导得
    2y+2z·zy′-z-(x+y)zy′-2+2zy′=0②
    ①②中,令zx′=0,zy′=0,解得x=(z+2)/2,y=(z+2)/2,将其代入已知方程得Z=±4,故驻点为(3,3)和(-1,-1)。
    ①式两边对x,y分别求导得
    2+2(zx′)2+2zzxx″-2zx′+(2-x-y)zxx″=0③
    2zy′zx′+2zzxy″-zy′-zx′+(2-x-y)zxy″=0④
    ②式两边对y求导得
    2+2(zy′)2+2zzyy″-2zy′+(2-x-y)zyy″=0⑤
    当x=y=-1,z=-4时,zx′=zy′=0,将其代入③④⑤,得A=zxx″(-1,-1)=1/2,B=zxy″(-1,-1)=0,C=zyy″(-1,-1)=1/2,B2-AC=-1/4<0,A=1/2>0。
    则函数z在(-1,-1)处取得极小值z=-4。
    当x=y=3,z=4时,zx′=zy′=0,并将其代入③④⑤,得A=zxx″(3,3)=-1/2,B=zxy″(3,3)=0,C=zyy″(3,3)=-1/2,B2-AC=-1/4<0,A=-1/2<0。
    故z在(3,3)点处取到极大值z=4。
    解析： 暂无解析

  • 第20题：

    单选题
    已知方程x2y2＋y＝1（y＞0）确定y为x的函数，则（　　）。
    A

    y（x）有极小值，但无极大值

    B

    y（x）有极大值，但无极小值

    C

    y（x）既有极大值又有极小值

    D

    无极值


    正确答案： C
    解析：
    方程x2y2＋y＝1（y＞0），两边对x求导得2xy2＋2x2y·y′＋y′＝0。y′＝0时，x＝0（y＞0）。再次求导得2y2＋4xy·y′＋4xy·y′＋2x2·（y′）2＋2x2y·y″＋y″＝0。故x＝0时，y＝1，y′（0）＝0，y″（0）＝－2＜0，则函数在x＝0点取得极大值，又因函数只有一个驻点，所以函数无极小值。

  • 第21题：

    填空题
    已知函数y＝y（x）由方程ey＋6xy＋x2－1＝0所确定，则y″（0）＝____。

    正确答案： -2
    解析：
    ey＋6xy＋x2－1＝0两边对x求导，得ey·y′＋6xy′＋6y＋2x＝0①。两边再对x求导，得ey·y″＋ey（y′）2＋6xy″＋12y′＋2＝0②。当x＝0时，y＝0，将x＝0，y＝0代入①得y′（0）＝0，再将x＝y＝y′（0）＝0代入②得y″（0）＝－2。

  • 第22题：

    填空题
    设函数y＝y（x）由方程exy＋ln[y/（x＋1）]＝0所确定，则y′（0）＝____。

    正确答案： (e-1)/e2
    解析：
    exy＋ln[y/（x＋1）]＝0方程两边对x求导，得exy（y＋xy′）＋y′/y－1/（x＋1）＝0。当x＝0时，y＝e－1。将x＝0，y＝e－1代入上式，得y′（0）＝（e－1）/e2。

  • 第23题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    x－y＝0

    B

    x＋y＝0

    C

    －x－y＝0

    D

    －x＋y＝0


    正确答案： C
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

相关内容