设Ω是由平面x+y+z=1与三个坐标平面所围成的空间区域,则=_________.
题目
设Ω是由平面x+y+z=1与三个坐标平面所围成的空间区域,则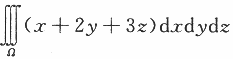 =_________.
=_________.
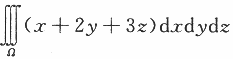 =_________.
=_________.相似考题
更多“设Ω是由平面x+y+z=1与三个坐标平面所围成的空间区域,则=_________.”相关问题
-
第1题:
设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·
①求平面图形的面积;
②求平面图形D绕x轴旋转一周所成旋转体的体积Vx.答案:解析: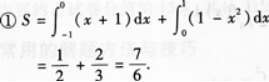
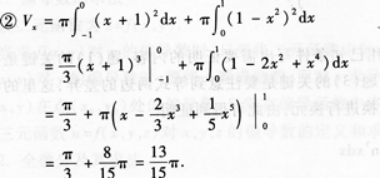
-
第2题:
设D是由曲线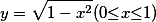 与
与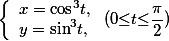 围成的平面区域,求D绕x轴转一周所得转体的体积和表面积.答案:解析:由于
围成的平面区域,求D绕x轴转一周所得转体的体积和表面积.答案:解析:由于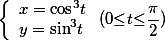 ,则可以化成直角坐标系下的方程,可得
,则可以化成直角坐标系下的方程,可得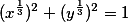 ,从而有
,从而有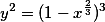 所以有
所以有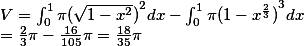 : 表面积
: 表面积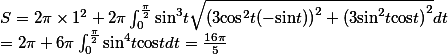
-
第3题:
设封闭曲线L的极坐标方程为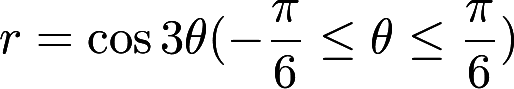 ,则L所围成的平面图形的面积为答案:解析:
,则L所围成的平面图形的面积为答案:解析: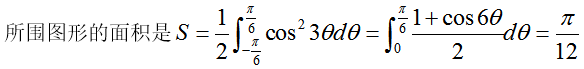
-
第4题:
设L为球面x^2+y^2+z^2=1与平面x+y+z=0的交线,则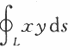 =_________.答案:解析:利用第一类曲线积分的轮换对称性.
=_________.答案:解析:利用第一类曲线积分的轮换对称性.
-
第5题:
设Ω是由锥面x^2+(y-2)^2=(1-z)^2(0≤x≤1)与平面z=0围成的锥体,求Ω的形心坐标.答案:解析:
-
第6题:
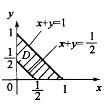
设平面闭区域D由x=0,y=0,x+y=1/2,x+y=1 所围成。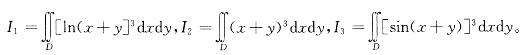 A.I123
A.I123
B. I132
C. I321
D. I312答案:B解析:提示 为了观察方便,做出平面区域D的图形,区域D在直线x+y=1的下方,在直线x+y=1/2上方以及由直线x= 0,y = 0围成。积分区域D上的点满足1/2≤x+y≤1。
故ln(x+y) ≤0,[ln(x+y)]3 ≤0
由三角函数知识,当0故033
所以平面区域D上的点满足:
[ln(x+y)]33 3
由二重积分性质: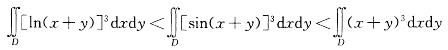
-
第7题:

x轴旋转一周,所成旋转曲面记作S。
(1)在空间直角坐标系下,写出曲面S的方程;
(2)求曲面S与平面x=0所围成立体的体积。答案:解析:
-
第8题:
设区域D是由直线y=x,x=2,y=1围成的封闭平面图形,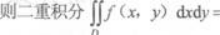
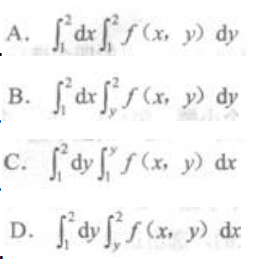 答案:D解析:积分区域如右图中阴影部分所示.D可以表示为1≤x≤2,1≤y≤x或1≤y≤2,y≤x≤2.对照所给选项,知应选D.
答案:D解析:积分区域如右图中阴影部分所示.D可以表示为1≤x≤2,1≤y≤x或1≤y≤2,y≤x≤2.对照所给选项,知应选D.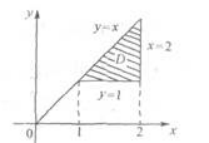
-
第9题:
在过点P(1,3,6)的所有平面中,有一平面,使之与三个坐标平面所围四面体的体积最小值是( )。A.18
B.48
C.72
D.81答案:D解析:
-
第10题:
空间主体上的平面是由直线围成的封闭线框,所以平面的投影可化解为()的投影进行作图。
正确答案:各条直线段 -
第11题:
填空题室内活动区域是指在居住空间内,由距地面或楼板面为()和(),距内墙内表面(),距外墙内表面或固定的采暖空调设备()的所有平面所围成的区域。正确答案: 100mm,1800mm,300mm,600mm解析: 暂无解析 -
第12题:
单选题地面点的空间位置是由()来表示的。A地理坐标
B平面直角坐标
C坐标和高程
D高斯平面直角坐标
正确答案: B解析: A、地理坐标B、平面直角坐标C、坐标和高程D、高斯平面直角坐标 -
第13题:
由曲线y=x3,直线x=1,z轴围成的平面有界区域的面积为_________.答案:解析:【答案】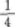
【考情点拨】本题考查了积分的应用的知识点.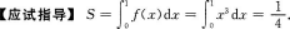
-
第14题:
设平面内区域D由直线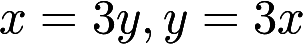 及
及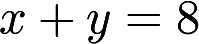 围成.计算
围成.计算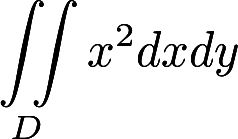 答案:解析:
答案:解析: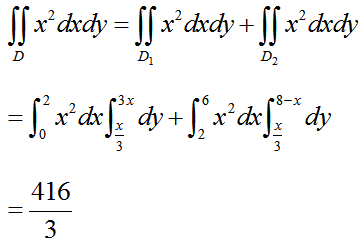
-
第15题:
设有界区域Ω由平面2x+y+2z=2与三个坐标平面围成,∑为Ω整个表面的外侧,计算曲面积分.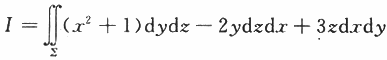 答案:解析:【解】由高斯公式得
答案:解析:【解】由高斯公式得
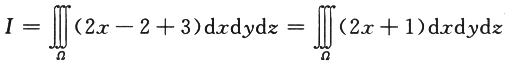
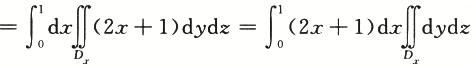
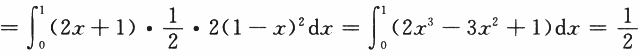
.
【评注】在三重积分的计算中,用先二后一积分较为简单,当然也可化为三次积分计算. -
第16题:
设直线L过A(1,0,0),B(0,1,1)两点,将L绕z轴旋转一周得到曲面∑,∑与平面z=0,z=2所围成的立体为Ω.
(Ⅰ)求曲面∑的方程;
(Ⅱ)求Ω的形心坐标.答案:解析:【分析】利用定义求旋转曲面∑的方程;利用三重积分求Ω的形心坐标.
-
第17题:
设D是两个坐标轴和直线x+y=1所围成的三角形区域,则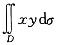 的值为:
的值为:
 答案:C解析:提示:画出积分区域D的图形,把二重积分化为二次积分,
答案:C解析:提示:画出积分区域D的图形,把二重积分化为二次积分,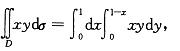 ,计算出最后答案。
,计算出最后答案。 -
第18题:
将平面曲线y=x2分别绕y轴和x轴旋转一周,所得旋转曲面分别记作S1和S2。
(1)在空间直角坐标系中,分别写出曲面S1和S2的方程;
(2)求平面y=4与曲面S1。所围成的立体的体积。答案:解析:(1)在空间直角坐标系中,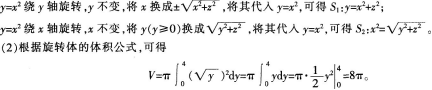
-
第19题:
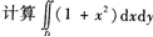
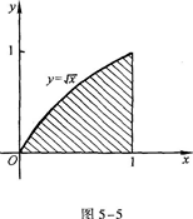
,其中D是由
及x轴所围成的平面区域.答案:解析:积分区域D如图5-5所示.若选择先对Y积分后对x积分,区域D可以表示为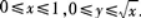
因此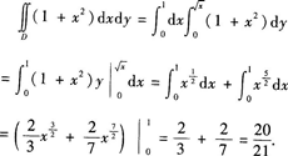
-
第20题:
计算二重积分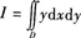
,其中D是由直线
及y=1围
成的平面区域.答案:解析:所给积分区域D如图5-6所示,如果选择先对y积分后对x积分的二次积分,需要将积分区域划分为几个子区域,如果选择先对x积分后对y积分的二次积分,区域D可以表示为
0≤y≤1,Y≤x≤y+1,
因此
【评析】
上述分析通常又是选择积分次序问题的常见方法.

-
第21题:
地面点的空间位置是由()来表示的。
- A、地理坐标
- B、平面直角坐标
- C、坐标和高程
- D、高斯平面直角坐标
正确答案:C -
第22题:
平面体是由若干个平面所围成的形体,是具有()、()、()三个方向尺度的几何体,它的每个表面都是平面。
正确答案:长度、宽度、高度 -
第23题:
填空题平面都是由若干个平面所围成的几何形体,称为()。正确答案: 平面基本体解析: 暂无解析
