itgle.com

设某种零件的长度L～N(18,4),从一大批这种零件中随机取出10件,求这10件中长度在16～22之间的零件数X的概率分布、数学期望和方差.

题目
设某种零件的长度L～N(18,4),从一大批这种零件中随机取出10件,求这10件中长度在16～22之间的零件数X的概率分布、数学期望和方差.

相似考题

1.某种零件的长度和质量的相关系数为0.97，更换材料后每个零件质量均降低0.3克，而长度不变，那么此种零件的长度与质量的相关系数为( )。A．0.5B．0.67C．0.97D．-0.97

2.（ⅱ）求这2个零件直径相等的概率。

3.分批零件法适用于( )。A、零件数量较多B、零件数量不多C、成批生产D、大批生产E、装配式复杂生产

4.（Ⅱ）从一等品零件中，随机抽取2个.（ⅰ）用零件的编号列出所有可能的抽取结果；

更多“设某种零件的长度L～N(18,4),从一大批这种零件中随机取出10件,求这10件中长度在16～22之间的零件数X的概率分布、数学期望和方差.”相关问题

  • 第1题：

    零件的主视图反映了零件的()。

    A、长度和宽度

    B、宽度和高度

    C、长度和高度

    D、长度、宽度和高度


    参考答案：C

  • 第2题：

       从一批零件毛坯中抽取出10件，称得它们的质量如下（单位：克）：

                400.0     400.3     401.2     398.9     399.8

                399.8     400.0     400.5     399.7     399.8

         求这10个零件的平均质量。


    平均质量为400g

  • 第3题：

    已知离散型随机变量X的概率分布为

    (1)求常数a；
    (2)求X的数学期望EX及方差DX．


    答案：
    解析：
    (1)因为0．2+a+0．2+0．3=1，所以a=0．3．(4分)(2)E=0×0．2+10×0．3+20×0．2+30×0．3=16，(7分)
    DX=(0-16)2×0．2+(10-16)2×0．3+(20-16)2×0．2+(30-16)2×0．3=124．(10分)

  • 第4题：

    设离散型随机变量x的分布列为

    ①求常数a的值；
    ②求X的数学期望E(X)．


    答案：
    解析：
    ①随机变量的分布列必须满足规范性，所以0．2+a+0．5=1，得a=0．3．②E(X)=1×0．2+2×0．3+3×0．5=2．3．

  • 第5题：

    设随机变量X1,X2,…,Xn相互独立且在［0,na］上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.


    答案：
    解析：

  • 第6题：

    已知一批零件的长度X(单位：cm)服从正态分布N(μ，1)，从中随机地抽取16个零件，得到长度的平均值为40(cm)，则μ的置信度为0.95的置信区间是_______.(注：标准正态分布函数值φ(1.96)=0.975，φ(1.645)=0.95.)


    答案：1、(39.51，40.49).
    解析：
    区间估计不是经常考的一个考点，一般都考单个正态总体方差已知条件下，求期望值μ的置信区间问题，置信区间为：，其中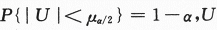～N(0，1).　　现题给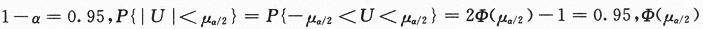=0.975，查得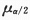=1.96.将σ=1，n=16,=40，代入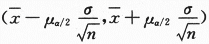得置信区间

  • 第7题：

    设总体X服从正态分布N(μ，σ^2)(σ>0)，从该总体中抽取简单随机样本X1，X2，…，Xn(n≥2)，其样本均值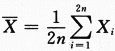,求统计量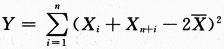的数学期望E(Y).


    答案：
    解析：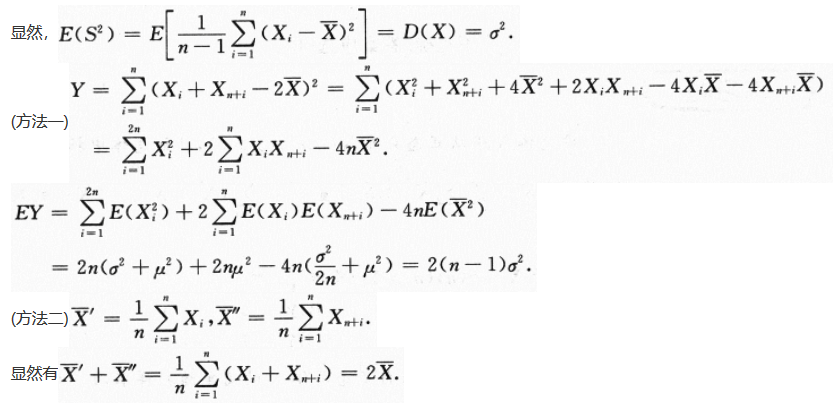

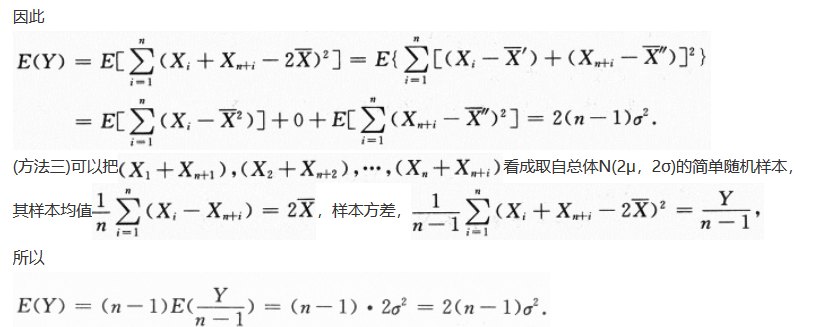
  • 第8题：

    设随机变量X的概率密度为令随机变量，
    　　(Ⅰ)求Y的分布函数；
    　　(Ⅱ)求概率P{X≤Y}.


    答案：
    解析：
    【分析】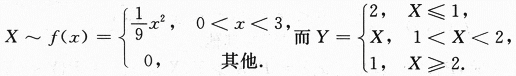
    Y是随机变量X的函数，只是这函数是分段表示的，这样得到的Y可能是非连续型，也非离散型，
    【解】(Ⅰ)设Y的分布函数为FYy)，显然P{1≤Y≤2}=1，所以，
    当y<1时，FY(y)=P{Y≤y)=0；
    当1≤y<2时，FY(y)=P{Y≤y}=P{Y<1}+P{Y=1}+P{1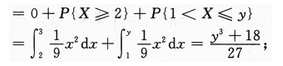
    当2≤y时，FY(y)=P{Y≤y}=P{Y≤2}=1.
    总之，Y的分布函数为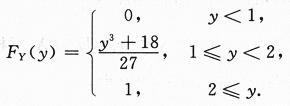

    (Ⅱ)因为Y=

  • 第9题：

    设随机变量X的分布函数为求随机变量X的概率密度和概率


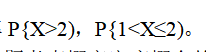    答案：
    解析：
    解：本题考查概率密度概念的简单应用。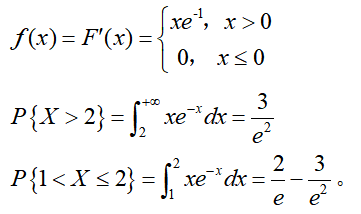

  • 第10题：

    批量是指（）。

    • A、每批投入制造的零件数
    • B、每年投入制造的零件数
    • C、一个工人一年加工的零件数
    • D、在一个产品中的零件数

    正确答案:A

  • 第11题：

    某手表厂在某段时间内生产100万个某种零件，用纯随机抽样方式不重复抽取1000个零件进行检验，测得废品为20件。如以99.73%概率保证，试对该厂这种零件的废品率作定值估计和区间估计。


    正确答案:2%，(0.68%，3.32%)

  • 第12题：

    单选题
    已知一批零件的长度X（单位：cm）服从正态分布N（μ，1），从中随机地抽取16个零件，得到长度的平均值为40（cm），则μ的置信度为0.95的置信区间是（）.
    A

    （37.51，42.49）

    B

    （39.51，40.49）

    C

    （35.51，44.49）

    D

    （36.51，43.49）


    正确答案： C
    解析： 暂无解析

  • 第13题：

    设X服从λ=2的泊松分布,则x的数学期望和方差分别是多少?


    答案：E(5X-1) = 5EX - 1 = 9 -> EX = λ = 2期望的基本性质，和泊松分布的期望公式而已。


  • 第14题：

    某种零件的长度服从正态分布。已知总体标准差σ=1．5，从总体中抽取200个零件组成样本，测得它们的平均长度为8．8厘米。试估计在95%置信水平下，全部零件平均长度的置信区间。


    正确答案：
    已知n=200，ψ=8．8，1-α=0．95，α=0．05， 
    当=0．025时，zα/2=z0．025=1．96
    根据题意，该题为双侧估计，μ的置信区间为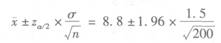 

    所以，总体均值μ在0．95置信水平下的置信区间为(8．59，9．01)

  • 第15题：

    设离散型随机变量X的概率分布为

    求X的数学期望EX及方差DX．


    答案：
    解析：

  • 第16题：

    一批零件中有10个合格品，3个次品，安装机器时，从这批零件中任取一个，取到合格品才能安装．若取出的是次品，则不再放回，求在取得合格品前已取出的次品数X的概率分布．


    答案：
    解析：
    由题意，X的可能取值为0，1，2，3．X=0，即第一次就取到合格品，没有取到次品，P{X=0}=；X=1，即第一次取到次品，第二次取到合格品，P{X=1}=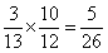；同理，P{X=2)=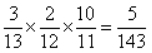；P{X=3}=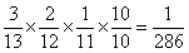

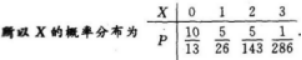
  • 第17题：

    设随机变量X的概率密度为
    　　
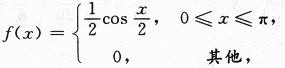
    　　对X独立地重复观察4次，用Y表示观察值大于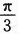的次数，求Y^2的数学期望.


    答案：
    解析：
    【简解】如果将观察X理解为试验，观察值大于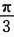理解为试验成功，则Y表示独立地重复试验4次成功的次数，即Y～B(4，p)
    其中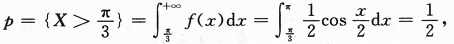

  • 第18题：

    一工人同时独立制造三个零件,第k个零件不合格的概率为（k=1,2,3）,以随机变量X表示三个零件中不合格的零件个数,则P（X=2)=_______.


    答案：
    解析：
    令Ak={第k个零件不合格}（k=1，2，3），　则

  • 第19题：

    设总体X服从正态分布N（μ,σ^2）(σ>0),X1,X1,…,Xn为来自总体X的简单随机样本,令Y=.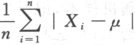,求Y的数学期望与方差


    答案：
    解析：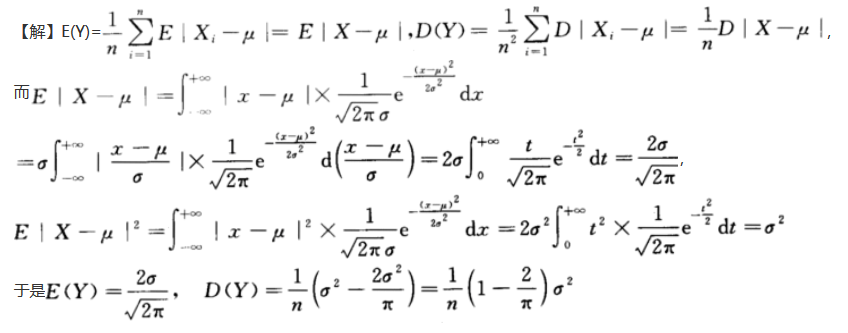

  • 第20题：

    设随机变量x的概率密度为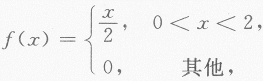F(x)为X的分布函数，EX为X的数学期望，则P{F(X)>EX-1}=________.


    答案：
    解析：

  • 第21题：

    数学期望本意即为随机变量分布的（）

    • A、总体均值
    • B、总体方差
    • C、概率
    • D、均值

    正确答案:A

  • 第22题：

    若随机变量X服从参数为n和p的二项分布，则它的数学期望为（），方差是（）


    正确答案:np；npq

  • 第23题：

    已知一批零件的长度X（单位：cm）服从正态分布N（μ，1），从中随机地抽取16个零件，得到长度的平均值为40（cm），则μ的置信度为0.95的置信区间是（）.

    • A、（37.51，42.49）
    • B、（39.51，40.49）
    • C、（35.51，44.49）
    • D、（36.51，43.49）

    正确答案:B

相关内容