itgle.com

一枚硬币掷三次，出现两次正面在上的概率是A.0.25 B.0.375 C.0.50 D.0.625

题目
一枚硬币掷三次，出现两次正面在上的概率是

A.0.25
B.0.375
C.0.50
D.0.625
相似考题

1.将一枚硬币投掷两次，至少出现一次正面的概率为（ ）。A．0.25B．0.50C．0.75D．1.00

2.掷均匀硬币一次,事件“出现正面或反面”的概率为________。A．0.1B．0.5C．0.4D．1

3.一枚硬币掷3次,出现两次或两次以上正面的概率是()。A.0.1B.0.9C.0.8D.0.5

4.掷硬币两次，事件“全是正面或全是反面”的概率是( )。A．1/4B．1/2C．3/4D．1

更多“一枚硬币掷三次，出现两次正面在上的概率是”相关问题

  • 第1题：

    一枚硬币投掷三次，或三枚硬币各掷一次，出现两次或两次以上正面的概率是1/2。()


    参考答案：正确

  • 第2题：

    投一枚硬币三次，问恰好有两次正面一次反面的概率是多少？（ ）

    A．4/5

    B．2/3

    C．3/8

    D．1/2


    正确答案：C
    一枚硬币投三次共有8种结果，用1表示为正面，0表示反面，则有(0，0，0)，(0，0，1)，(0，1，0)，(1，0，0)，(1，1，0)，(1，0，1)，(0，1，1)，(1，1，1)种结果，可以看到满足条件的结果有3种，概率是3/8。

  • 第3题：

    关于频率与概率有下列几种说法
    ①“明天下雨的概率是90％”，表示明天下雨的可能性很大
    ②“抛一枚硬币正面朝上的概率为50％”，表示每抛两次硬币就有一次正面朝上
    ③“某彩票中奖的概率是1％”，表示买10张该种彩票不可能中奖
    ④“抛一枚硬币正面朝上的概率为50％”，表示随着抛掷硬币次数的增加，“抛出正面朝上”这一事件发生的频率稳定在50％附近
    其中正确的说法是()。

    A.①④
    B.②③
    C.④
    D.①③

    答案：A
    解析：
    事件A的概率P(A)是对事件A发生可能性大小的一个度量，它是一个确定的数值，与试

  • 第4题：

    如下事件发生的概率等于1/4的是()。

    A:抛两枚普通的硬币，出现的均是正面
    B:一个不透明的袋子里装着黑白红蓝四种颜色的球，随机拿出一个恰好为红色球
    C:抛两枚普通的硬币，出现一个正面和一个反面
    D:掷一枚普通的骰子，出现点数小于3
    E:掷两枚普通的骰子，出现点数之和小于

    答案：A,B
    解析：
    A选项，出现两个都是正面的概率=1/2*1/2=1/4；B选项，考查古典概率计算方法的使用，随机拿出一个球可能有4种颜色，红色只占其中一种，所以拿出恰为红色球的概率=1/4；C选项，出现一个正面和一个反面应该包括两种情况：正反、反正，因此其概率=1/4+1/4=1/2；D选项，掷出的点数总共有6种情况，而小于3的只有l和2两种情况，所以其概率=2/6=1/3；E选项，掷两枚骰子，出现的点数和最小为2，即两枚骰子的点数都是1，因此其和小于2是不可能事件，所以概率=0。

  • 第5题：

    掷一枚均匀的硬币若干次，当正面向上次数大于反面向上次数时停止，则在4次之内停止的概率为



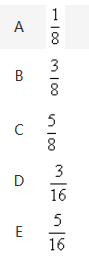    答案：C
    解析：

  • 第6题：

    某研究者抛投硬币10 000次，有5 042次正面在上，在另外的5 000次抛投中，有2 496次正面在上，此时研究者将0.50作为硬币正面在上的概率的估计值，这里的0.50属于

    A.先验概率
    B.古典概率
    C.真实概率
    D.后验概率

    答案：D
    解析：
    概率因寻求的方法不同有两种定义，分别是后验概率和先验概率。以随机事件A在大量重复试验中出现的稳定频率值作为随机事件A概率的估计值，这样寻得的概率称为后验概率或统计概率。先验概率是指当试验的所有可能结果有限且每一种结果出现的可能性相等时直接计算出来的概率，也称古典概率。例如，抛投硬币有两种结果，正面在上和正面在下，两种结果的可能性相等，此时计算出来的正面在上的先验概率是0.50。试验次数越多，后验概率越接近先验概率。

  • 第7题：

    一个硬币掷10次，其中5次正面向上的概率是0.5。


    正确答案:错误

  • 第8题：

    将一枚硬币独立地掷两次，引进事件：A1={掷第一次出现正面}，A2={掷第二次出现正面}，A3={正、反面各出现一次}，A4={正面出现两次}，则事件（）

    • A、A1，A2，A3相互独立
    • B、A2，A3，A4相互独立
    • C、A1，A2，A3两两独立
    • D、A2，A3，A4两两独立

    正确答案:C

  • 第9题：

    一枚硬币被投掷三次并且三次都是正面，第四次试验出现正面的概率（）

    • A、比出现背面的概率小
    • B、比出现背面的概率大
    • C、是1/16
    • D、是1/2

    正确答案:D

  • 第10题：

    一枚硬币被扔了3次，三次都是正面的概率是（）

    • A、0
    • B、0.500
    • C、0.875
    • D、0.125

    正确答案:D

  • 第11题：

    单选题
    掷硬币两次，事件“全是正面或全是反面”的概率是（　　）。
    A

    1/4

    B

    1/2

    C

    3/4

    D

    1


    正确答案： A
    解析： 掷硬币两次，样本空间为{（正面，正面），（正面，反面），（反面，正面），（反面，反面）}，故“全是正面或全是反面”的概率为2/4＝1/2。

  • 第12题：

    单选题
    下列事件中，必然事件是(　　)．
    A

    掷一枚硬币出现正面    

    B

    掷一枚硬币出现反面

    C

    掷一枚硬币，或者出现正面，或者出现反面  

    D

    掷一枚硬币，出现正面和反面


    正确答案： A
    解析： 根据必然事件的定义可以知道

  • 第13题：

    将一枚匀称的硬币连续掷两次，则正面只出现一次的概率为()

    A、1/3

    B、0.5

    C、0.6

    D、0.1


    参考答案：B


  • 第14题：

    （2）连续4次抛掷一枚硬币，求恰出现两次是正面的概率和最后两次出现是正面的概率。


    正确答案：
              

  • 第15题：

    计算以下事件的概率可以用古典概率方法解决的是()。

    A:明天是晴天的概率
    B:抛一枚硬币出现正面的概率
    C:明天股票上涨的概率
    D:某地发生交通事故的概率

    答案：B
    解析：
    可以使用古典概率方法计算概率的事件需具备三个条件：事件可能产生的结果是有限的，所有结果之间两两互不相容的，所有的结果发生都是等可能的。依据这三个条件，只有B项符合。

  • 第16题：

    一枚硬币抛三次，恰好出现两次正面的概率是多少？()

    A.1/8
    B.3/8
    C.1/4
    D.1/2

    答案：B
    解析：
    推断统计；推断统计的数学基础。 一枚硬币抛掷三次可能出现的结果共8种，每种结果出现的可能为1／8，出现两次正面的情况有3种，故而两次正面的概率为3/8。

  • 第17题：

    投掷两次硬币，出现“正面，反面”的概率是()。

    A:0.50
    B:0.33
    C:0.25
    D:0.125

    答案：C
    解析：
    整个事件包括第一次出现正面，第二次出现反面，且两个结果不相关，所以直接用概率的乘法计算。P(AB)=P(A)*P(B)=1/2*1/2=1/4。

  • 第18题：

    将一枚硬币投掷两次，至少出现一次正面的概率为（ ）。
    A. 0. 25 B. 0.50 C. 0.75 D. 1.00


    答案：C
    解析：

  • 第19题：

    一枚硬币被扔了三次，如果三次都是正面，此时第四次出现正面的概率是（）。

    • A、0
    • B、1/16
    • C、1/2
    • D、大于背面的概率

    正确答案:C

  • 第20题：

    对掷一枚硬币的试验，“出现正面”称为（）。

    • A、随机事件
    • B、必然事件
    • C、不可能事件
    • D、样本空间

    正确答案:A

  • 第21题：

    抛掷一枚均匀的硬币，出现正面的概率是（）。

    • A、0
    • B、1
    • C、0.5
    • D、0.8

    正确答案:C

  • 第22题：

    随机投掷一枚硬币，则两次都正面朝上的概率是（）。

    • A、1/4
    • B、1/2
    • C、3/4
    • D、1

    正确答案:A

  • 第23题：

    单选题
    掷均匀硬币一次，事件“出现正面或反面”的概率为（　　）。
    A

    0.1

    B

    0.4

    C

    0.5

    D

    1


    正确答案： B
    解析： 掷硬币一次，不是出现正面，就是出现反面，所以事件“出现正面或反面”为必然事件，其概率为1。

相关内容