itgle.com

已知齐次线性方程组（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.

题目
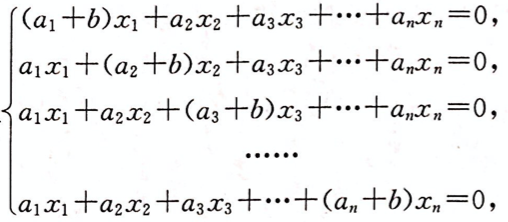
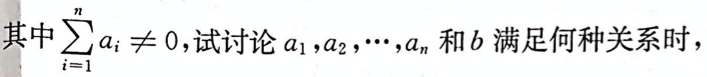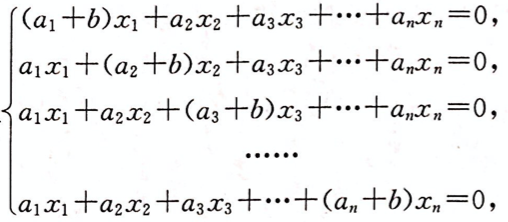
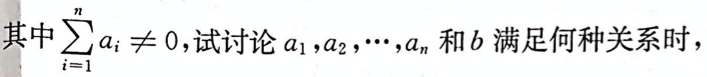已知齐次线性方程组（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.

相似考题

1.若齐次线性方程组中方程的个数小于未知数的个数,则该方程组必有非零解。()此题为判断题(对，错)。

2.非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()

3.设A是m×N阶矩阵,B是n×m阶矩阵,则().A.当m>n时,线性齐次方程组ABX=0有非零解 B.当m>n时,线性齐次方程组ABX=0只有零解 C.当n>m时,线性齐次方程组ABX=0有非零解 D.当n>m时,线性齐次方程组ABX=0只有零解

4.设线性方程组AX=b有唯一解,则相应的齐次方程组AX=0解的情况是()。A.有非零解B.只有零解C.无解D.解不能确定

参考答案和解析
答案：
解析：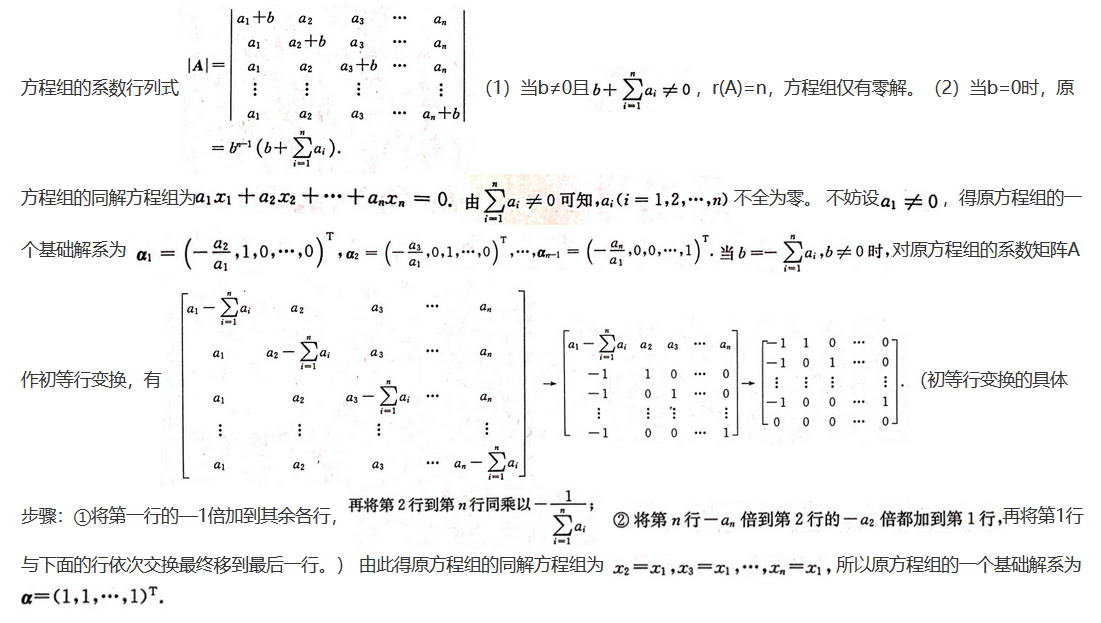
更多“已知齐次线性方程组（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.”相关问题

  • 第1题：

    设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。

    A.若Ax=0仅有零解，则Ax=b有惟一解
    B.若Ax=0有非零解，则Ax=b有无穷多个解
    C.若Ax=b有无穷多个解，则Ax=0仅有零解
    D.若Ax=b有无穷多个解，则Ax=0有非零解

    答案：D
    解析：

  • 第2题：

    设A是m×n阶矩阵,下列命题正确的是().

    A.若方程组AX=0只有零解,则方程组AX=b有唯一解
    B.若方程组AX=0有非零解,则方程组AX=b有无穷多个解
    C.若方程组AX=b无解,则方程组AX=0一定有非零解
    D.若方程组AX=b有无穷多个解,则方程组AX=0一定有非零解

    答案：D
    解析：

  • 第3题：

    设齐次线性方程组其中ab≠0,n≥2.讨论a,b取何值时,方程组只有零解、有无穷多个解？在有无穷多个解时求出其通解.


    答案：
    解析：

  • 第4题：

    λ和μ为何值时，齐次方程组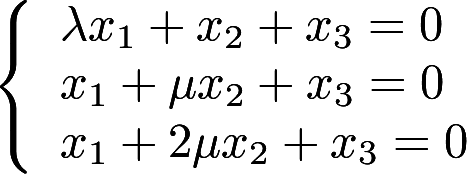有非零解?


    答案：
    解析：

  • 第5题：

    解非齐次线性方程组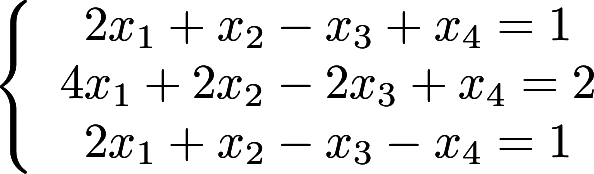


    答案：
    解析：

  • 第6题：

    已知非齐次线性方程组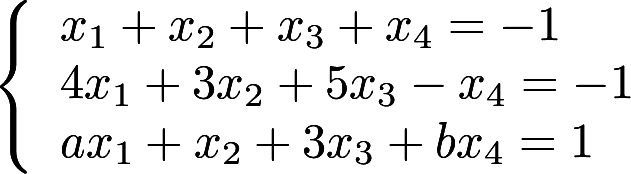 有3个线性无关的解. （Ⅰ）证明方程组系数矩阵A的秩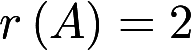； （Ⅱ）求的值及方程组的通解


    答案：
    解析：

  • 第7题：

    问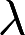取何值时 非齐次线性方程组， (1)有唯一解 (2)无解 (3)有无穷多个解，并在无穷多个解时，求方程组的通解


    答案：
    解析：

  • 第8题：

    设有齐次线性方程组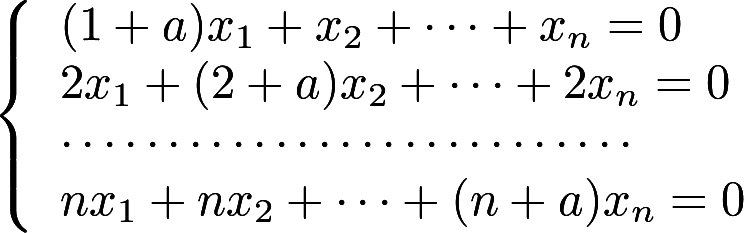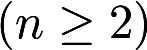.试问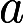取何值时，该方程组有非零解，并求出其通解


    答案：
    解析：

  • 第9题：

    设线性方程组(I)与(II)有公共的非零解,其中(I)为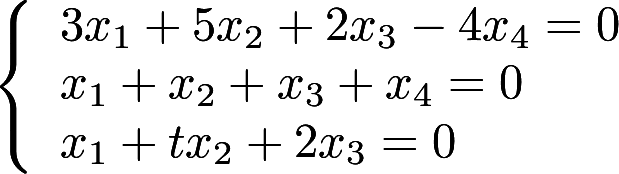，(II)有基础解系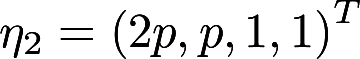，求p,t的值和全部公共解


    答案：
    解析：

  • 第10题：

    设非齐次线性方程组( I )的导出方程组为(II)，则()。

    A.当(I )只有唯一 解时，(II)只有零解
    B. (I )有解的充分必要条件是(II)有解
    C.当(I )有非零解时，(II)有无穷多解
    D.当(I)有非零解时，(I )有无穷多解

    答案：A
    解析：

  • 第11题：

    设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。

    • A、无解
    • B、只有零解
    • C、有非零解
    • D、不一定

    正确答案:C

  • 第12题：

    单选题
    n阶矩阵A的伴随矩阵为A*，齐次线性方程组AX(→)＝0(→)有两个线性无关的解，则（　　）。
    A

    A*X(→)＝0(→)的解均是AX(→)＝0(→)的解

    B

    AX(→)＝0(→)的解均是A*X(→)＝0(→)的解

    C

    AX(→)＝0(→)与A*X(→)＝0(→)无非零公共解

    D

    AX(→)＝0(→)与A*X(→)＝0(→)仅有2个非零公共解


    正确答案： A
    解析：
    由齐次方程组AX(→)＝0(→)有两个线性无关的解向量，知方程组AX(→)＝0(→)的基础解系所含解向量的个数为n－r（A）≥2，即r（A）≤n－2＜n－1。由矩阵A与其伴随矩阵秩的关系，知r（A*）＝0，即A*＝0。所以任意n维列向量均是方程组A*X(→)＝0(→)的解，故方程组AX(→)＝0(→)的解均是A*X(→)＝0(→)的解。

  • 第13题：

    设n阶矩阵A的伴随矩阵A^*≠0，若ζ1，ζ2，ζ3，ζ4是非齐次线性方程组Ax=b的互不相等的解，则对应的齐次线性方程组Ax=0的基础解系

    A.不存在.
    B.仅含一个非零解向量.
    C.含有两个线性无关的解向量.
    D.含有三个线性无关的解向量.

    答案：B
    解析：

  • 第14题：

    要使齐次线性方程组



    有非零解，则a应满足（　　）。

    A． －2＜a＜1
    B． a＝1或a＝－2
    C． a≠－1且a≠－2
    D． a＞1

    答案：B
    解析：
    齐次线性方程组的系数矩阵作初等变换如下



    要使齐次线性方程组有非零解，则矩阵的秩r＜3，因此得a－1＝0或－（a＋2）（a－1）＝0，计算得a＝1或a＝－2。
    【说明】n元齐次线性方程组Ax＝0有非零解的充要条件是r（A）＜n。

  • 第15题：

    求齐次线性方程组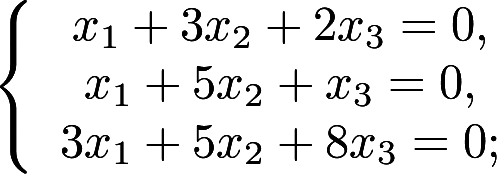的基础解系


    答案：
    解析：

  • 第16题：

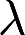    取何值时,非齐次线性方程组 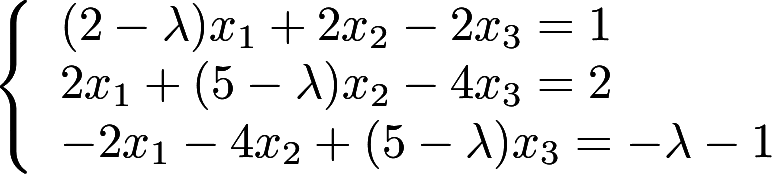(1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时，求方程组的通解。


    答案：
    解析：

  • 第17题：

    设齐次线性方程组
    　　
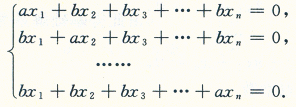
    　　其中a≠0，b≠0，n≥2.试讨论a，b为何值时，方程组仅有零解，有无穷多组解？在有无穷多组解时，求出全部解，并用基础解系表示全部解.


    答案：
    解析：

  • 第18题：

    设有齐次线性方程组
    　　
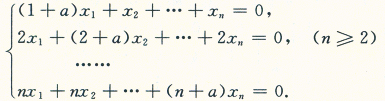
    　　试问a为何值时，该方程组有非零解，并求其通解.


    答案：
    解析：

  • 第19题：

    已知下列非齐次线性方程组(Ⅰ)，(Ⅱ)
    　　
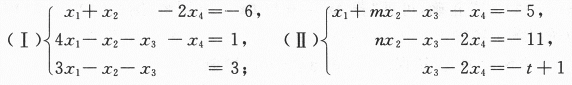
    　　(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解.
    　　(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.


    答案：
    解析：

  • 第20题：

    问：齐次线性方程组有非零解时，a,b必须满足什么条件？


    答案：
    解析：

  • 第21题：

    问取何值时，齐次方程组有非零解？


    答案：
    解析：

  • 第22题：

    求齐次线性方程组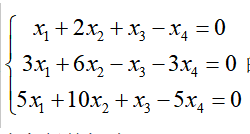的全部解（要求用基础解系表示）。


    答案：
    解析：
    解：本题考查齐次线性方程组的解法。

  • 第23题：

    单选题
    设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。
    A

    无解

    B

    只有零解

    C

    有非零解

    D

    不一定


    正确答案： A
    解析： AX=0有非零解的充要条件是R（A）＜6，而4×6矩阵的秩R（A）≤4，故AX=0有非零解，故选（C）。

相关内容