itgle.com

考虑一个具有如下生产函数的经济体：Y=AK0.4 L0.6，其中K为资本，L为劳动。 设A=1，计算人均生产函数。

题目
考虑一个具有如下生产函数的经济体：Y=AK0.4 L0.6，其中K为资本，L为劳动。 设A=1，计算人均生产函数。

相似考题

1.假若两个经济体采取的总量生产函数形式都为Y=AK^αL^(1－α),但是根据各自的禀赋结构(资本劳动比)选择最优的生产函数的资本密集,第一个经济体的资本为10000单位,第二个经济体的资本为100单位,第二经济体的劳动为10000单位,第一个经济体的劳动为100单位,那么第一个经济体的劳均收入是第二经济体的多少倍()。A.50倍B.100倍C.50^(2/3)倍D.约37倍

2.考虑一个具有如下生产函数的经济体：Y=AK0.4 L0.6，其中K为资本，L为劳动。 假设每年的折旧率δ为5%，考虑简单的索罗增长模型，稳态时，求出人均资本存量的黄金律以及该黄金律水平下的人均产量水平、人均投资水平、人均消费水平。

3.已知生产函数为Q =f(K，L)=KL -0. 5L2-0.32K2，Q表示产量，K表示资本，L表示劳动，若K =10，求： (1)写出劳动的平均产量和边际产量函数。 (2)计算当总产量达到极大值时企业雇佣的劳动人数。

4.在总量生产函数Y=AK^αL^(1－α)设定下,按照新结构生产理论的结构变迁方程内生最优生产函数之后,如果GDP(Y)为e^10,资本存量(K)为e^6,劳动(L)为e^3,索罗剩余(A)是()。A.e^4B.e^6C.e^7D.e^5

参考答案和解析
答案：
解析：
若A=1，则有生产函数为Y= K0. 4 L0.6，从而有：

此即为人均生产函数。
更多“考虑一个具有如下生产函数的经济体：Y=AK0.4 L0.6，其中K为资本，L为劳动。 设A=1，计算人均生产函数。”相关问题

  • 第1题：

    假定产出是根据含有失业率的生产函数Y= Kα[（l-u*）L]1-α 来表示的。在上式中，K为资本，L为劳动力，u*为自然失业率。国民储蓄率为s，劳动力增长率为n，资本折旧率为δ。 请把人均产出(y=Y/L)表示为人均资本(k=K/L)和自然失业率的函数。


    答案：
    解析：

  • 第2题：

    考虑如下经济模型：生产方程：Y=F(K,L)=KαL1-α其中K为资本存量，L为工人数量。产出的一部分被用于消费，另一部分是储蓄为S。所有的储蓄被用于投资。资本存量的折旧率为ζ。假设技术进步和人口增长均为零。计算稳态时的人均资本量，人均产出和人均消费


    答案：
    解析：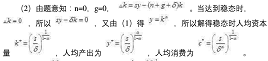

  • 第3题：

    设在新古典增长模型的框架下，生产函数为Y=F(K,L)=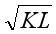

    (1)求人均生产函数y=f(k)。 (2)若不存在技术进步，求稳态下的人均资本量、人均产量和人均消费量。


    答案：
    解析：

  • 第4题：

    假定产出是根据含有失业率的生产函数Y= Kα[（l-u*）L]1-α 来表示的。在上式中，K为资本，L为劳动力，u*为自然失业率。国民储蓄率为s，劳动力增长率为n，资本折旧率为δ。 计算该经济的稳态的人均资本和人均产出。


    答案：
    解析：

  • 第5题：

    假定经济体的总量生产函数为Y=K0.5L0.5，在2012年，人均产出为4，投资率为0.5，劳动增长率为1%，资本折旧率为9%。 (1)经济体稳态的劳动资本存量是多少？ (2)黄金律水平的劳动资本存量是多少？ (3)画图分析这个经济体人均产出的可能变化趋势。


    答案：
    解析：
    (1)由总量生产函数可得人均生产函数为：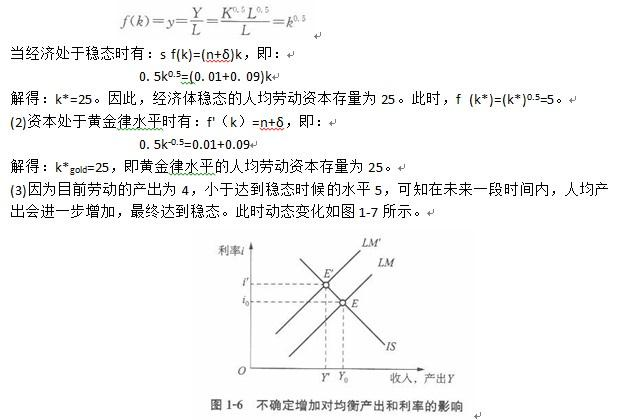

  • 第6题：

    已知新古典增长模型中人均生产函数为y=f(k) =2k-0. 5k2，最为人均资本，储蓄率s为0.4，人口增长率以为0.2%。 请计算： (1)经漭达到稳定状态的值。 (2)黄金律所要求的人均资本k值


    答案：
    解析：
    (1)经济达到稳态时，有k=sy-nk=0，解得k=3.99，即经济达到稳态时的人均资本存量为3. 99，人均产出为0.02。 (2)达到资本黄金律水平时，有MPK =n，解得k=1. 998，所以黄金律水平下的人均资本存量k=l. 998。

  • 第7题：

    已知生产函数y＝k－0.2k2，y为人均产出，k为人均资本存量。储蓄率为0.1，人口增长率为0.05，假设资本折旧为0，稳态时人均产出为（）。

    • A、1.2
    • B、1
    • C、1.25
    • D、1.5

    正确答案:C

  • 第8题：

    在新古典增长模型中，人均生产函数为y=f（k）=2k-0.5k*k，人均储蓄率为0.3，设人口增长率为3%。试求经济增长的k值。


    正确答案:均衡时有sf（k）=nk，
    即0.3*（2k-0.5k^2）=0.03k，
    解得k=3.8

  • 第9题：

    计算题：设一个国家的总量生产函数是：y=k其中y和k分别指人均产出和人均资本。如果储蓄率为28%，人口增长率为1%，技术进步率为2%，折旧率为4%，该国稳定状态的产出是多少？如果储蓄率下降到10%，而人口增长率上升到4%，其他不变，那么该国新的稳定状态产出又是多少？


    正确答案:当达到稳定状态时有：k=
    代入数据得：（4%+1%+2%）k=28%k
    从而人均资本稳态水平k=16
    从而产出y=4
    同理，当达到新的稳态时，得k=1
    从而新的产出水平y=1

  • 第10题：

    单选题
    设生产函数为Q＝ALαKβ，其中Q是产出量，L是劳动投入量，K是资本投入量，而A，α，β均为大于零的常数，则当Q＝1时，K对于L的弹性为（　　）。
    A

    β/α

    B

    －β/α

    C

    －α/β

    D

    α/β


    正确答案： A
    解析：
    由Q＝ALαKβ可知，Q＝1时，ln1＝lnA＋αlnL＋βlnK，两端对L求导，得0＝α/L＋βKL′/K，则η＝（L/K）·（dK/dL）＝－α/β。

  • 第11题：

    单选题
    已知生产函数y＝k－0.2k2，y为人均产出，k为人均资本存量。储蓄率为0.1，人口增长率为0.05，假设资本折旧为0，稳态时人均产出为（）。
    A

    1.2

    B

    1

    C

    1.25

    D

    1.5


    正确答案： C
    解析： 暂无解析

  • 第12题：

    问答题
    已知企业的生产函数为Q=F（L，K）=LK-0.5L2-0.32K2，Q表示产量，K表示资本，L表示劳动，令K=10。试求劳动的平均产量函数（AP1）和边际产量函数（MP1）。

    正确答案：
    当K=10时,短期生产函数为:Q=-0.5L2+10L-32
    因而劳动的平均产量函数为:APL=Q/L=-0.5L+10-32/L
    劳动的边际产量函数为:MPL=dQ/dL=-L+10
    解析： 您好，非常感谢您的反馈，本题的答案已完善。平均产量函数应为：AP=-0.5L+10-32/L。再次感谢。

  • 第13题：

    假设一个经济的人均生产函数为y=k，其中k为人均资本：求： (1)经济的总量生产函数。 (2)在没有人口增长和技术进步的情况下，假定年折旧率为δ=10%，储蓄率为s=40%。那么稳态下的人均资本、人均产出和人均消费分别为多少？


    答案：
    解析：

    稳态人均消费为c=（1-s）y=0.6 x4 =2.4．

  • 第14题：

    在索罗增长模型( Solow model)中，假设生产函数为柯布一道格拉靳函数Y=KaL1-a，已知n、g、б 、a。 (1)写出生产函数的简约形式y=f（k），其中y为人均产出，是为人均资本存量。 (2)已知s值，求解稳定状态下的y*、k*、c*。 (3)当s值未知时，求解黄金规则水平下的稳态y*、k*、s*、c*。


    答案：
    解析：

  • 第15题：

    假设生产函数为Y=KaL1-a，其中，a=l／3，K表示资本，L表示劳动力。 (1)该生产函数是否具有规模收益不变的特征？请解释。 (2)假设该经济的劳动力刚好等于总人口，请将上述生产函数变化成人均产出与人均资本之间的关系。 (3)假设该经济每年的储蓄率为8/25，资本每年的折旧率为2/25。求稳态人均资本和稳态人均产出。 (4)现假设资本折旧率变为1/12，其他假设不变，请问当经济实现稳态时，若要使人均消费最大化，该经济的储蓄率应该是多少？人均消费达到最大化时，该经济的人均资本是多少？此时的人均消费是多少？


    答案：
    解析：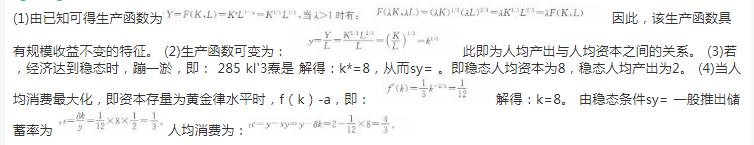

  • 第16题：

    考虑柯布一道格拉斯生产函数

    其中K袁示资本存量，L表示劳动量，要素价格分别是r和w。 (1)求短期成本函数STC(r，w，Y)（短期生产假定资本存量保持不变）。 (2)求长期成本函数LTC(r，w，Y)。 (3)讨论参数a、β的取值与规模报酬之间的关系。


    答案：
    解析：
    (1)厂商的短期总成本曲线是在保持r和w不变的前提下，根据k的 变化而得出的。 由题意可得：成本函数为C=wL+rK。当K-定时，最优状态为：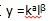

    (3)投入的增加导致产出相同比例的增加，这是规模报酬不变的情形；若产出增加比例小于投入增加比例，则是规模报酬递减的情形；如果产出增加的比例大于投入增加的比例，则是规模报酬递增的情形。 柯布一道格拉斯生产函数的规模报酬取决于系数a和口的值，即有：

    因此，a+β>l，柯布道格拉斯生产函数为规模报酬递增；口+J9—1，函数为规模报酬不变；a+β<1，函数为规模报酬递减。

  • 第17题：

    考虑一个具有如下生产函数的经济体：Y=AK0.4 L0.6，其中K为资本，L为劳动。 在一般化(A不等于常数)的生产函数中，你认为A可能包含哪些影响经济长期增长的因素，这些是否可能与资本K或劳动L相关？


    答案：
    解析：
    在一般化的生产函数中，A可能包含技术进步和经济结构等影响经济长期增长的因素，这些可能与资本或劳动相关：此时，消费并不能增加，因此，政策没有作用或者说作用大打折扣，与第(2)问的结论相反。

  • 第18题：

    在新古典增长模型中，生产函数为y=f(k)=2k-0. 5k2，人均储蓄率为s-0.3，设人口增长率为3%，求：(1)使经济均衡增长的k值。(2)黄金律所要求的人均资本量。


    答案：
    解析：
    (1)生产函数为y= f(k)一2k -0. 5k2，人均储蓄率为0.3，人口增长率为n=3%。当经济达到稳态时有：△k=s厂(k)-nk=0.3×（2k-0. Sk2)-0. 03k-0解得稳态时的人均资本水平： k-3.8 (2)当经济达到资本黄金律水平时有MPK=n，即有：2-k=3%解得黄金律所要求的人均资本存量为：K*gold=1. 97

  • 第19题：

    已知某经济社会生产函数y=k-0.2k2，y为人均产出，k为人均资本存量。平均储蓄倾向s为0.1，人口增长率n为0.05，求 （1）均衡资本——劳动比率； （2）均衡人均产出、均衡人均储蓄和均衡人均消费


    正确答案:（1）不考虑折旧和技术进步时，在稳定状态有k*=sy-nk=s（k-0.2k2）-nk=0，因k>0，将等式s（k-0.2k2）-nk=0整理，得：k=5-5n/s=2.5，因此，均衡资本——劳动比率为2.5；
    （2）将k=2.5代入生产函数中，得到均衡人均产出y=1.25，均衡人均储蓄sy=0.125，均衡人均消费c=y-sy=1.125

  • 第20题：

    已知某企业的生产函数为Q=50L^（3/5）K^（3/5）（Q为产量，L为劳动，K为资本），则（）

    • A、生产函数为规模报酬递增
    • B、生产函数为规模报酬递减
    • C、生产函数为规模报酬不变
    • D、生产要素报酬递增
    • E、生产要素报酬递减

    正确答案:A,E

  • 第21题：

    问答题
    在新古典增长模型中，集约化生产函数为Y=f（k）=2k-0.5k2，人均储蓄率为0.3，设人口增长率为3%，求：（1）使经济均衡增长的k值；（2）黄金分割律所要求的人均资本量。

    正确答案：
    (1)经济均衡增长时,有sf(k)= nk,将s=0.3,n=3%代入,可得:
    0.3(2k-0.5k2)=0.03k
    化简得:20k-5k2=k,解得:k=3.8。
    (2)按黄金分割律要求,对每个人的资本量的选择应使得资本的边际产品等于劳动的增长率,即f′(k)=n。
    于是有2-k=0.03,解得k=1.97,即为与黄金率相对应的稳态的人均资本量。
    解析： 暂无解析

  • 第22题：

    问答题
    已知某经济社会生产函数y=k-0.2k2，y为人均产出，k为人均资本存量。平均储蓄倾向s为0.1，人口增长率n为0.05，求 （1）均衡资本——劳动比率； （2）均衡人均产出、均衡人均储蓄和均衡人均消费

    正确答案： （1）不考虑折旧和技术进步时，在稳定状态有k*=sy-nk=s（k-0.2k2）-nk=0，因k>0，将等式s（k-0.2k2）-nk=0整理，得：k=5-5n/s=2.5，因此，均衡资本——劳动比率为2.5；
    （2）将k=2.5代入生产函数中，得到均衡人均产出y=1.25，均衡人均储蓄sy=0.125，均衡人均消费c=y-sy=1.125
    解析： 暂无解析

  • 第23题：

    填空题
    设生产函数为Q＝ALαKβ，其中Q是产出量，L是劳动投入量，K是资本投入量，而A，α，β均为大于零的常数，则当Q＝1时，K对于L的弹性为____。

    正确答案： -α/β
    解析：
    由Q＝ALαKβ可知，Q＝1时，ln1＝lnA＋αlnL＋βlnK，两端对L求导，得0＝α/L＋βKL′/K，则η＝（L/K）·（dK/dL）＝－α/β。

相关内容