一个垄断厂商生产某种产品的成本函数为：C=5+3Q，将其产品在两个地理分割的市场上销售，这两个市场对该产品的需求函数分别为：P1=15-Q1，P2=25-2Q2。该垄断厂商将针对两个市场制定何种价格策略？两个市场各自能够销售多少产品？厂商实现多少总利润？在两个市场分别造成多少福利损失？

题目

相似考题

1.考虑一个双寡头古诺模型，p和Q分别表示市场价格和产品销售总量；q1和q2分别表示厂商1和厂商2的产量；MC表示厂商生产的边际成本，假设两个厂商生产的产品完全同质。如果两个厂商同质，且在均衡价格上的需求弹性（以绝对值定义）为2，那么均衡时厂商的价格加成率是多少？

2.已知生产相同商品的潜在生产者的成本函数都是C（qi）= 25 +lOqi，市场需求函数为Q=Il0 -P，qi，表示各生产者的产量，P表示市场价格：假定各生产者组成的寡头市场满足古诺模型的要求，试求： (1)若只有两个生产者组成吉诺模型的寡头市场，产品市场的均衡价格等于多少？每个企业能获得多少垄断利润？ (2)若各潜在生产者在寡头市场展开竞争，从而形成垄断竞争市场，产品市场的均衡价格等于多少？在垄断竞争的产品市场上，最终可能存在几个生产者？ (3)政府向垄断竞争市场的生产者的每个产品征收75元的商品税时，产品市场的均衡价格等于多少？在垄断竞争市场上，最终可能存在几个生产者？

3.垄断厂商生产某一产品，产品的成本函数为C(q)=q2，市场反需求函数为p=120-q。试求：(1)垄断厂商利润最大化的产量和价格，并画图说明。(2)政府对垄断厂商征收100元的税收后，垄断厂商的产量和价格。(3)政府对垄断厂商单位产品征收从量税2元，垄断厂商的产量和价格。

4.某产品的市场需求曲线为Q=2O -P，市场中有n个生产成本相同的厂商，单个厂商的成本函数为c=2q2+2，问： (1)若该市场为竞争性市场，市场均衡时的市场价格和单个企业的产量是多少？ (2)长期均衡时该市场中最多有多少个厂商？ (3)若该市场为寡头垄断市场，古诺均衡时的市场价格和单个企业的产量是多少？

参考答案和解析

答案：

解析：

更多“一个垄断厂商生产某种产品的成本函数为：C=5+3Q，将其产品在两个地理分割的市场上销售，这两个市场对该产品的需求函数分别为：P1=15-Q1，P2=25-2Q2。该垄断厂商将针对两个市场制定何种价格策略？两个市场各自能够销售多少产品？厂商实现多少总利润？在两个市场分别造成多少福利损失？ ”相关问题

第1题：

假定某垄断厂商生产一种产品，其总成本函数为TC=0.SQ2 +10Q +5，市场的反需求函数为P=70 -2Q： (1)求该厂商实现利润最大化时的产量、产品价格和利润量。 (2)如果要求该垄断厂商遵从完全竞争原则，那么，该厂商实现利润最大化时的产量、产品价格和利润量又是多少？ (3)试比较(1)和(2)的结果，你可以得出什么结论？

答案：
解析：
(1)厂商边际成本函数为MC=Q+10，边际收益函数为MR =70 -4Q。根据利润最大化原则MR =MC，可知Q =12，P=46，利润π=PQ - TC= 355。 (2)根据完全竞争原则可知P=MC，可得Q =20，P=30，此时利润π= PQ - TC= 195。 (3)比较(1)和(2)可知，垄断条件下的利润更大，价格更高，但产量却比较低。
第2题：

某垄断厂商生产产品X的边际成本和平均成本均为常数c，所生产的X产品在两个分割的市场上销售，这两个市场的需求函数分别是P1=a1 – bq1和P2= a2 – bq2，其中，a1> a2>c>0，且3a2> a1+2c。证明：（1）该厂商无论实行三级价格歧视还是统一定价，总产量水平相同。（2）若统一定价时的价格为P，三级价格歧视时两个市场的价格分别是P1和P2，则P1>P>P2。

答案：
解析：
如果厂商实行三级价格歧视定价，则其实现利润最大化时需要满足的条件是MR1=MR2=MC，且MR1=a 1– 2bq1 ，MR2= a2 –2 bq2则：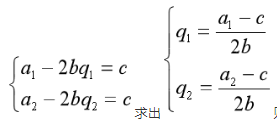

则厂商得总产量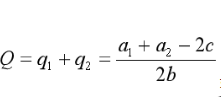

如果厂商现在实行统一定价，则厂商面临得整个市场需求曲线由两个市场得需求曲线水平加总得到：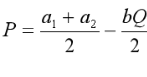

厂商实现利润最大化时需满足MR=MC原则，即：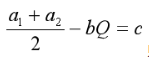

则可得厂商统一定价时得产量为：

可以看出不论是实行三级价格歧视还时统一定价厂商得产量总是相同得，均为

根据（1）问当中得结论可知厂商：厂商在实行三级价格歧视时在两个市场得价格分别为：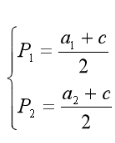

厂商在实行统一定价时厂商出售商品得价格为：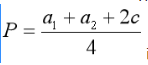

已知a1> a2>c>0，且3a2> a1+2c，则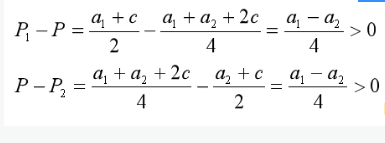

因此P1>P>P2
第3题：

考虑一个双寡头古诺模型，p和Q分别表示市场价格和产品销售总量；q1和q2分别表示厂商1和厂商2的产量；MC表示厂商生产的边际成本，假设两个厂商生产的产品完全同质。如果两个厂商的生产均面临不变的边际成本1/2，且反需求曲线为p=1-Q，则均衡时两个企业的产量分别是多少？

答案：
解析：
第4题：

一个垄断厂商生产某种产品的成本函数为：C=5+3Q，将其产品在两个地理分割的市场上销售，这两个市场对该产品的需求函数分别为：P1=15-Q1，P2=25-2Q2。假设企业被禁止使用价格歧视策略，那么该企业将采取何种价格策略？能够在两个市场各自销售多少产品？两个市场总共实现多少利润？在两个市场上分别造成多少福利损失？

答案：
解析：
第5题：

假设两个分割的市场，其市场需求曲线分别是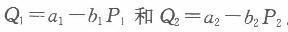

某完全垄断厂商以MC=AC=C的常数边际成本C来生产。若该垄断者在这两个分割市场上实行三级价格歧视，其最优产出水平为QD；若该垄断者不实行价格歧视而统一供给这两个市场，其最优产出水平为QM。 (1)判断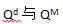

的相对大小 (2)解释该垄断者实行价格歧视的理由。

答案：
解析：
本题主要考查三级价格歧视与统一定价条件下的产量水平以及利润水平的比较，常以计算题的形式出现，考生应重点掌握。本题与高鸿业《西方经济学（微观部分）》第7章“不完全竞争的市场”课后习题第6题非常相似，建议考生平时多做题，熟悉解题思路。

(1)由已知可得两市场的反需求曲线分别为：

利润最大化的一阶条件为：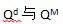

解得：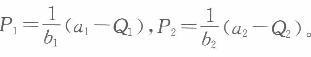

从而可得：

若垄断者不实行价格歧视，则P=P1=P2，此时总的市场需求函数为：Q=Q1+Q2=a1+a2-(b1+b2)P 则反市场需求函数为：
第6题：

某垄断企业面对政府保护的国内市场和竞争激烈的国际市场这两个分割的市场，在国内市场，其产品的需求方程为

在国际市场上，其产品的需求方程为

假设厂商的边际成本MC=60+Q/10 ，其中Q= qd+qC。 (1)求该生产厂商的最优产出和国内国际市场所占的份额。 (2)求在国内国际市场的价格与需求价格弹性。 (3)假如国内和国际市场合并为一个市场，这时总产出与价格是多少？

答案：
解析：
第7题：

某产品市场的需求曲线为Q=1000-10P，成本函数为C=40Q，下列说法正确的有()。
Ⅰ．若该产品由一个垄断厂商生产，则利润最大化时产量是300
Ⅱ．若该产品由一个垄断厂商生产，则厂商最大利润为9000
Ⅲ．若要实现帕累托最优，相应的产量是600，价格是40
Ⅳ．在垄断条件下，社会福利的净损失是5000

A.Ⅰ、Ⅱ
B.Ⅰ、Ⅲ、Ⅳ
C.Ⅲ、Ⅳ
D.Ⅰ、Ⅱ、Ⅲ

答案：D
解析：
垄断厂商进行生产决策的条件为MR=MC，由于TR=PQ=100Q-0．1Q2，所以MR=dTR／dQ=100-0．2Q，MC=dC／dQ=40，进而解得Q=300，P=70，最大利润为：300×70-40×300=9000；价格等于边际成本时实现帕累托最优，P=40，Q=600；垄断条件下消费者剩余为：300 x 30／2—4500，帕累托最优下消费者剩余为：600×60／2=18000，消费者剩余减少18000-4500=13500，垄断利润增加9000，所以社会福利的净损失为：13500-9000=4500。
第8题：

一个歧视性垄断厂商在两个市场上销售，假设不存在套利机会，市场1的需求曲线为P1=100-Q1／2，而P2=100-Q2，垄断厂商的总产量用Q=Q1+Q2表示，垄断厂商的成本函数依赖于总产出，TC(Q)=Q2。在利润最大化时，下列说法正确的是(　　)。
Ⅰ．垄断厂商在市场1的产量Q1为30
Ⅱ．垄断厂商在市场2的产量Q2为12．5
Ⅲ．歧视性垄断的利润水平是1875
Ⅳ．垄断厂商的总产量为37．5

A.Ⅱ、Ⅲ、Ⅳ
B.Ⅰ、Ⅱ
C.Ⅰ、Ⅱ、Ⅲ、Ⅳ
D.Ⅰ、Ⅲ、Ⅳ

答案：A
解析：
第9题：

一个歧视性垄断厂商在两个市场上销售，假设不存在套利机会，市场1的需求曲线为P1=100-Q1／2，而P2=100-Q2，垄断厂商的总产量用Q=Q1+Q2表示，垄断厂商的成本函数依赖于总产出，TC(Q)=Q2，下列说法正确的有（　　）。
Ⅰ 垄断厂商在市场1的产量Q1为30
Ⅱ 垄断厂商在市场2的产量Q2为12．5
Ⅲ 歧视性垄断的利润水平是1875
Ⅳ 垄断厂商的总产量为37．5

A.Ⅱ、Ⅲ、Ⅳ
B.Ⅰ、Ⅱ
C.Ⅰ、Ⅱ、Ⅲ、Ⅳ
D.Ⅰ、Ⅲ、Ⅳ

答案：A
解析：

@##
第10题：

某完全垄断厂商生产和销售A产品，当该厂商销售一个单位的A产品时，商品价格为12元；当销售两个单位的A产品时，商品价格为10元；当销售三个单位的A产品时，其边际收益为4元。如果销售四个单位的A产品时平均收益为6元，总收益价格和边际收益分别是多少？

正确答案: TR=AR×Q=6×4=24元
P=TR/Q=24/4=6元
MR=△TR/△Q=（6×4-8×3）/1=0
第11题：

某寡头垄断市场上有两个厂商，总成本均为自身产量的20倍，市场需求函数为Q=200-P。若两个厂商达成协议垄断市场，共同安排产量，则各自的利润情况如何？

正确答案:200-2Q=20，Q=90，Q1=Q2=45
第12题：

问答题
某垄断者的产品在两个分割市场出售，产品的成本函数和两个市场的需求函数分别为TC＝Q2＋10Q，Q1＝32－0.4P1，Q2＝18－0.1P2，其中Q＝Q1＋Q2。　　（1）假设两个市场能实行差别价格，求解利润最大时的两个市场的售价、销售量和利润。　　（2）假设两个市场只能索取相同价格，求解利润最大时的售价、销售量和利润。

正确答案： (1)由成本函数可得出边际成本为:MC=TC′=2(Q₁+Q₂)+10。
由需求函数可得出反需求函数分别为:
P₁=80-2.5Q₁,P₂=180-10Q₂
TR₁=P₁Q₁=(80-2.5Q₁)Q₁,可得出:MR₁=80-5Q₁;
TR₂=P₂Q₂=(180-10Q₂)Q₂,可得出:MR₂=180-20Q₂。
根据三级价格歧视利润最大化均衡条件MR₁=MR₂=MC,即有:
80-5Q₁=180-20Q₂=2(Q₁+Q₂)+10
解得:Q₁=8,Q₂=7,Q=15。
将销售量分别代入各自的反需求函数,可得:P₁=60,P₂=110。
厂商利润:π=P₁Q₁+P₂Q₂-TC=60×8+110×7-15²-10×15=875。
(2)若两个市场只能卖同一价格,即P₁=P₂,则:
Q=Q₁+Q₂=32-0.4P+18-0.1P=50-0.5P
由需求函数可得出反需求函数为:P=100-2Q。
TR=PQ=(100-2Q)Q,可得出:MR=100-4Q。
根据利润最大化均衡条件MR=MC,解得:Q=15。
将销售量代入反需求函数,可得:P=70。
在这一价格下,Q₁=4,Q₂=11,说明当P=70时厂商在两个市场上都售出了产品。
厂商利润π=PQ-TC=70×15-15²-10×15=675。
解析：暂无解析
第13题：

考虑一个小产品市场，其中假定男性市场对小产品的总需求曲线为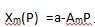

女性市场对小产品的总需求曲线为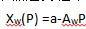

这里假定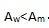

每件小产品的生产成本为c。 (1)假定小产晶市场是完全竞争的，求市场均衡时的价格和各自市场的需求量。 (2)设厂商甲是该小产品的垄断生产者，另假定厂商甲被禁止采取“价格歧视”政策（即对男性和女性分别定价），则使利润最大化的价格是多少？在怎样的条件下，男、女性都有正的需求量？ (3)仍设厂商甲是该小产品的垄断生产者，若允许厂商甲进行价格歧视，求出其对男性和女性分别的最优定价。

答案：
解析：
第14题：

假定某寡头市场有两个厂商生产同种产品，市场的反需求函数为P=100—Q，两个厂商的成本函数分别为TC1=20Q，TC2=0.5Q22。 (1)假定两厂商按古诺模型行动，求两厂商各自的产量和利润量，以及行业的总利润量。 (2)假定两厂商联合行动组成卡特尔，追求共同利润最大化，求两厂商各自的产量和利润量，以及行业的总利润量。 (3)比较(1)与(2)的结果。

答案：
解析：
(1)对于第一个厂商而言： π1= PQ1 - TC1
第15题：

一个垄断企业面临两个分离的市场。市场1的需求函数为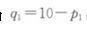

市场2的需求函数为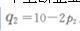

垄断厂商生产的边际成本为1，不存在固定成本。 (1)假定垄断厂商可以实施三级价格歧视。求两个市场的利润最大化垄断价格和产量以及垄断厂商的总利润，两个市场的消费者剩余之和，以及总剩余之和。（总剩余定义为总消费者剩余加上总利润） (2)假定垄断厂商不能实施价格歧视而只能在两个市场收取统一的价格。求利润最大化的垄断价格和产量以及垄断厂商的总利润，两个市场的消费者剩余之和，以及总剩余之和。（提示：你需要确定垄断者在两个市场都销售是否是最优的） (3)对于本题中所描述的需求状况，三级价格歧视对社会有益吗？请加以解释。（注意：不能仅仅比较数值大小）

答案：
解析：
(1)由已知可得两个市场的反需求函数分别为：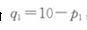

对应的两个市场的边际收益分别为：

若垄断厂商实施三级价格歧视，利用两个市场利润最大化原则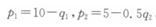

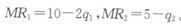
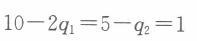
(3)三级价格歧视下，厂商利润更大；在同一价格策略下，消费者剩余更大。但是，在三级价格歧视下，社会总剩余小于同一价格策略的社会总剩余。可以看出，实施三级价格歧视对于厂商和市场2的消费者是有益的，对于市场1的消费者是有害的。
第16题：

已知某垄断厂商利用一个工厂生产一种产品，其产品在两个分割的市场出售，它的成本函数为TC =O. 5Q2 +7Q，两个市场的需求函数分别为Q1=30 -0. 5P1、Q2=100 - 2P2． (1)求当该厂商实行三级价格歧视时，它追求利润最大化前提下的两个市场各自的销售量、价格，以及厂商的总利润（保留整数部分）。 (2)求当该厂商在两个市场上实行统一的价格时，它追求利润最大化前提下的销售量、价格，以及厂商的总利润（保留整数部分）。 (3)比较(1)和(2)的结果。

答案：
解析：
(1)第一个市场的反需求函数为P1=60 -2Q．，边际收益函数为MR1= 60 -4Q,。第二个市场的反需求函数为P2= 50 -0.5Q2，边际收益函数为MR2= 50 - Q2。边际成本函数为MC=Q+7，根据三级价格歧视利润最大化的原则，有： MR1= MR2= MC

(2)市场需求函数为： Q=Q1+ Q2=(30 -0. 5P)+ (100 - 2P)= 130 -2. 5P 市场反需求函数为P= 52 -0. 4Q，边际收益函数为MR =52 -0. 8Q。根据最大化原则MR =MC，可得Q +7= 52 -0. 8Q，Q=25。价格P=42，总利润为π=PQ - TC =563。 (3)比较(1)和(2)的结果可以看到，三级价格歧视下利润大于统一定价下的利润，这表明实行三级价格歧视要比不这样做更为有利可图。
第17题：

一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3（Q1+Q2），东部市场对该产品的需求函数为P1=15-Q1，西部市场对该产品的需求函数为P2=25一2Q2。如果政府规定，禁止在不同市场上制定不同的价格，求此时该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。

答案：
解析：
第18题：

一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3（Q1+Q2），东部市场对该产品的需求函数为P1=15-Q1，西部市场对该产品的需求函数为P2=25一2Q2。如果该厂商可以将东西部市场区分开，在不同的市场制定不同的价格出售，求该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。

答案：
解析：
第19题：

一个歧视性垄断厂商在两个市场上销售产品，假设不存在套利机会，市场1的需求曲线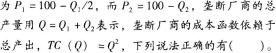

A.Ⅱ、Ⅲ、Ⅳ
B.Ⅰ、Ⅱ
C.Ⅰ、Ⅱ、Ⅲ、Ⅳ
D.Ⅰ、Ⅲ、Ⅳ

答案：A
解析：
第20题：

某产品市场的需求曲线为Q=1000-10P，成本函数为C=40Q，则下列结论正确的有（）。
?Ⅰ.若该产品由一个垄断厂商生产，则利润最大化时产量是300，价格是70
?Ⅱ.若该产品由一个垄断厂商生产，则厂商最大利润为9000
?Ⅲ.若要实现帕累托最优，相应的产量是600，价格是40
?Ⅳ.在垄断条件下，社会福利的净损失是5000

A.Ⅰ、Ⅱ、Ⅲ
B.Ⅰ、Ⅲ、Ⅳ
C.Ⅰ、Ⅱ
D.Ⅲ、Ⅳ

答案：A
解析：
该产品为垄断厂商生产时，市场需求函数即该厂商的需求函数。由Q=1000-10P得P=100-0.1Q得边际收益函数MR=100-0.2Q由成本函数C=40Q得MC=40=AC利润极大时，MC=MR，即40=100-0.2Q得Q=300，P=70，π=70×300-40×300=9000
即产量、价格和利润分别为300，70和9000
要达到帕累托最优，则价格必须等于边际成本，即P=100-0.1Q=40=MC，得Q=600，P=40
当Q=300，P=70时，消费者剩余为=300（85-70）=4500当Q=600，P=40时，消费者剩余为CS=600（70-40）=18000
社会福利的纯损失为：18000-4500-9000=4500在此，18000-4500=13500是垄断所造成的消费者剩余的减少量。
其中9000转化为垄断者利润，因此，社会福利的纯损失为4500。
第21题：

一个市场中有许多厂商生产和销售有差别的同种产品，而每个厂商对自己的产品价格都具有一定的垄断力量，称之为（）。

A、垄断市场
B、竞争市场
C、垄断竞争市场
D、寡头市场

答案：C
解析：
本题考查的是市场效率与市场失灵。垄断竞争市场是指一个市场中有许多厂商生产和销售有差别的同种产品，而每个厂商对自己的产品价格都具有一定的垄断力量。寡头市场是指少数几家厂商控制产品生产和销售的市场结构。
第22题：

某寡头垄断市场上有两个厂商，总成本均为自身产量的20倍，市场需求函数为Q=200-P。若两个厂商同时决定产量，产量分别是多少？

正确答案:分别求反应函数，180-2Q1-Q2=0，180-Q1-2Q2=0，Q1=Q2=60
第23题：

问答题
垄断厂商在两个分离的市场上销售产品，两个市场的需求函数分别为：Q1＝105－P1，Q2＝300－5P2。厂商的成本函数为：TC＝140＋15Q。如果厂商在两个市场上只能收取相同的价格，求利润最大时的售价。

正确答案：设厂商在两个市场上的产品价格均为P,即P₁=P₂=P,则市场需求Q=Q₁+Q₂=405-6P,从而反需求函数为P=(405-Q)/6,边际收益MR=67.5-Q/3。又边际成本MC=15,则根据厂商获得利润最大化的条件即MR=MC,得67.5-Q/3=15,解得Q=157.5,代入反需求函数得P=(405-157.5)÷6=41.25。因此,厂商利润最大时的售价为41.25。
解析：暂无解析

itgle.com

题目

相似考题

参考答案和解析

相关内容