设f(x),f'(x)为已知的连续函数，则微分方程y'十f'(x)y=f(x)f'(x)的通解是： A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +c C. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)

题目

设f(x),f'(x)为已知的连续函数，则微分方程y'十f'(x)y=f(x)f'(x)的通解是：
A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +c
C. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)

相似考题

1.设F是属性组U上的一组函数依赖，下列叙述正确的是A．若YX，则X→Y为F所逻辑蕴含B．若XU，则X→Y为F所逻辑蕴含C．若X→Y为F所逻辑蕴含，且ZU，则X→YZ为F所逻辑蕴含D．若X→Y及Y→Z为F所逻辑蕴含，则X→Z为F所逻辑蕴含

2.设F是属性组U上的一组函数依赖，下列叙述正确的是A．若，则X→Y为F所逻辑蕴含B．若，则X→Y为F所逻辑蕴含C．若X→Y为F所逻辑蕴含，且，则X→YZ为F所逻辑蕴含D．若X→Y及Y→Z为F所逻辑蕴含，则X→Z为F所逻辑蕴含

3.设F是属性组U上的一组函数依赖,下列叙述正确的是A．若Y∈U则X→Y为F所逻辑蕴含B．若X∈U则X→Y为F所逻辑蕴含C．若X→Y为F所逻辑蕴含,且Z∈U则X→YZ为F所逻辑蕴含D．若X→Y及X→Z为F所逻辑蕴含,则X→Z为F所逻辑蕴含

4.设y=f(－x),则y`=()。A.f`(x)B.-f`(x)C.f`(-x)D.-f`(-x)

参考答案和解析

答案：C

解析：

提示:对关于y、y'的一阶线性方程求通解。其中p(x)=f'(x)、Q(x) =f(x)*f'(x) 利

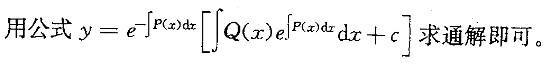
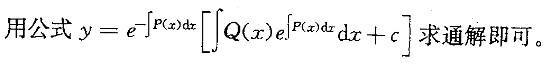
更多“设f(x),f'(x)为已知的连续函数，则微分方程y'十f'(x)y=f(x)f'(x)的通解是： ”相关问题

第1题：

设f1（x）和f2（x）为二阶常系数线性齐次微分方程y"+py'+q=0的两个特解，若由f1（x）和f2（x）能构成该方程的通解，下列哪个方程是其充分条件？

A.f1（x） *f'2（x）-f2（x）f'1（x）=0
B.f1（x） * f’2（x）-f2（x） *f'1（x）≠0
C.f1（x）f'2（x）+f2（x）*f'1（x） =0
D.f1（x）f'2（x）+f2（x）*f'1（x） ≠0

答案：B
解析：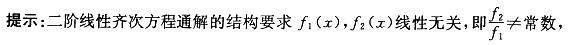
第2题：

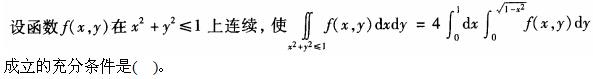A.f(-x，y)=f(x，y)，f(x，-y)=-f(x，y)
B.f(-x，y)=f(x，y)，f(x，-y)=f(x，y)
C.f(-x，y)=-f(x，y)，f(x，-y)=-f(x，y)
D.f(-x，y)=-f(x，y)，f(x，-y)=f(x，y)

答案：B
解析：
要求f(x，y)关于x和y都是偶函数。
第3题：

设关系模式R＜U，F＞，其中U为属性集，F是U上的一组函数依赖，那么Armstrong公理系统的伪传递律是指（）。

A.若X→Y，Y→Z为F所蕴涵，则X→Z为F所蕴涵
B.若X→Y，X→Z，则X→YZ为F所蕴涵
C.若X→Y，WY→Z，则XW→Z为F所蕴涵
D.若X→Y为F所蕴涵，且Z?U，则XZ→YZ为F所蕴涵

答案：C
解析：
本题考查关系数据库基础知识。从已知的一些函数依赖，可以推导出另外一些函数依赖，这就需要一系列推理规则。函数依赖的推理规则最早出现在1974年W.W.Armstrong的论文里，这些规则常被称作“Armstrong公理”。选项A“若X→Y，Y→Z为F所蕴涵，则H为F所蕴涵”符合Armstrong公理系统的传递率。选项B“若X→Y，X→Z，则X→YZ为F所蕴涵”符合Armstrong公理系统的合并规则。选项C“若X→Y，WY→Z，则XW→Z为F所蕴涵”符合Armstrong公理系统的伪传递率。选项D“若X→Y为F所蕴涵，且K?U，则XZ→YZ为F所蕴涵”符合Armstrong公理系统的增广率。
第4题：

已知微分方程y’+y=f(x)，其中f(x)是R上的连续函数.
　　(Ⅰ)若f(x)=x，求方程的通解.
　　(Ⅱ)若f(x)是周期为T的函数，证明：方程存在唯一的以T为周期的解.

答案：
解析：
【解】(Ⅰ)若f(x)=x，则方程为y'+y=x通解为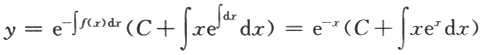

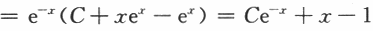
(Ⅱ)设y(x)为方程的任意解，则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T，有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0，有(e^x［y(x+T)-y(x)］)'=0，
即e^x［y(x+T)=y(x)］=C.取C=0得y(x+T)-y(x)=0，
y(x)为唯一以T为周期的解.
第5题：

非负连续函数f(x)满足f(0)=0,f(1)=1.已知以曲线y=f(x)为曲边，以[0,x]为底的曲边梯形，其面积与f(x)的n+1次幂成正比，则f(x)的表达式为

答案：
解析：
第6题：

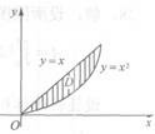
设f(x，y)为连续函数，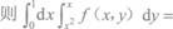

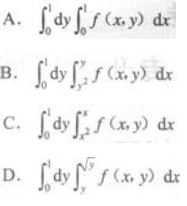答案：D
解析：
积分区域D可以由0≤x≤1，x2≤y≤x表示，其图形为右图中阴影部分．
第7题：

设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z=max{X，Y}的分布函数为（）
- A、F²（x）
- B、F（x）F（y）
- C、1-[1-F（x）]²
- D、[1-F（x）][1-F（y）]
正确答案:A
第8题：

单选题
设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（　　）。
A
f″（x）＋f（x）＝0
B
f′（x）＋f（x）＝0
C
f″（x）＋f′（x）＝0
D
f″（x）＋f′（x）＋f（x）＝0

正确答案： A
解析：
由f′（x）＝f（π/2－x），两边求导得f″（x）＝－f′（π/2－x）＝－f[π/2－（π/2－x）]＝－f（x），即f″（x）＋f（x）＝0。
第9题：

填空题
设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为____。

正确答案： f″(x)+f(x)=0
解析：
由f′（x）＝f（π/2－x），两边求导得f″（x）＝－f′（π/2－x）＝－f[π/2－（π/2－x）]＝－f（x），即f″（x）＋f（x）＝0。
第10题：

填空题
设f（x，y）＝ax＋by，其中a，b为常数，则f[xy，f（x，y）]＝____。

正确答案： axy+abx+b²y
解析：
由f（x，y）＝ax＋by知，f[xy，f（x，y）]＝axy＋b（ax＋by）＝axy＋abx＋b²y。
第11题：

单选题
设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z＝max{X，Y}的分布函数为（　　）。
A
F²（x）
B
F（x）F（y）
C
1－[1－F（x）]²
D
[1－F（x）][1－F（y）]

正确答案： C
解析：
F_Z（x）＝P{Z≤x}＝P{max（X，Y）≤x}＝P{X≤x，Y≤x}＝P{X≤x}·P{Y≤x}＝F²（x），故应选A。
第12题：

单选题
设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（　　）。
A
f′（x）＋f（x）＝0
B
f′（x）－f（x）＝0
C
f″（x）＋f（x）＝0
D
f″（x）－f（x）＝0

正确答案： D
解析：
由f′（x）＝f（π/2－x），两边求导得f″（x）＝－f′（π/2－x）＝－f[π/2－（π/2－x）]＝－f（x），即f″（x）＋f（x）＝0。
第13题：

下列( )项是在D={(x，y)|x2+y2≤1，x≥0，y≥0)上的连续函数f(x，y)，且f(x，y)=3(x+y)+16xy。

A.f(x，y)=3(x+y)+32xy
B.f(x，y)=3(x+y)-32xy
C.f(x，y)=3(x+y)-16xy
D.f(x，y)=3(x+y)+16xy

答案：B
解析：
解本题的关键在于搞清二重积分

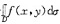
是表示一个常数，对f(x，y)=3(x+y)+

利用极坐标进行二重积分计算
第14题：

设f（x）、f'（x）为已知的连续函数，则微分方程y'+ f'（x）y = f（x）f'（x）的通解是：

答案：C
解析：
提示：对关于y、y'的一阶线性方程求通解。其中P（x）=f'（x）、Q（x）=f（x） * f'（x），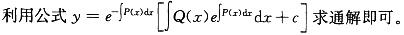
第15题：

设随机变量X，Y独立同分布，且X的分布函数为F(x)，则Z=max{X，Y}的分布函数为

A.AF^2(x)
B.F(x)F(y)
C.1-［1-F(x)］^2
D.［1-F(x)］［1-F(y)］

答案：A
解析：
随机变量Z=max(X，Y)的分布函数Fz(x)应为Fz(x)=P{Z≤x}，由此定义不难推出Fz(x).【求解】故答案应选(A).
【评注】不难验证(B)F(x)F(y)恰是二维随机变量(X，Y)的分布函数.(C)1-［1-F(x)］^2则是随机变量min(X，Y)的分布函数.(D)［1-F(x)］［1-F(y)］本身不是分布函数，因它不满足分布函数的充要条件.
第16题：

设f（x，y）为连续函数，则等于：

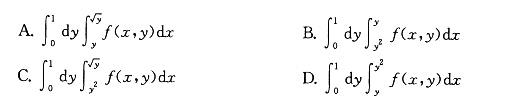答案：B
解析：
提示：画出积分区域D的图形，再按先x后y顺序写成二次积分。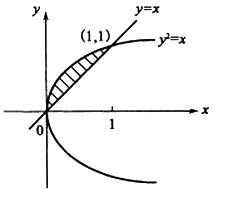
第17题：

设f（x）为区间[a，b]上的连续函数，则曲线y=f（x）与直线x=a，x=b，y=0所围成的封闭图形的面积为（）.《》（）

答案：B
解析：
本题考查的知识点为定积分的几何意义.由定积分的几何意义可知应选B.常见的错误是选C.如果画个草图，则可以避免这类错误.
第18题：

若连续函数y=f（x）在x₀点不可导，则曲线y=f(x)在（x₀,f(x₀））点没有切线.

正确答案:错误
第19题：

单选题
设f1（x）和f2（x）为二阶常系数线性齐次微分方程y″+py′+q=0的两个特解，若由f1（x）和f2（x）能构成该方程的通解，下列哪个方程是其充分条件？（）
A
f1（x）f′2（x）-f2（x）f′1（x）=0
B
f1（x）f′2（x）-f2（x）f′1（x）≠0
C
f1（x）f′2（x）+f2（x）f′1（x）=0
D
f1（x）f′2（x）+f2（x）f′1（x）≠0

正确答案： C
解析：暂无解析
第20题：

单选题
设f1（x），f2（x）是二阶线性齐次方程y″＋p（x）y′＋q（x）y＝0的两个特解，则c1f1（x）＋c2f2（x）（c1，c2是任意常数）是该方程的通解的充要条件为（　　）。
A
f₁（x）f₂′（x）－f₂（x）f₁′（x）＝0
B
f₁（x）f₂′（x）＋f₁′（x）f₂（x）＝0
C
f₁（x）f₂′（x）－f₁′（x）f₂（x）≠0
D
f₁′（x）f₂（x）＋f₂（x）f₁（x）≠0

正确答案： A
解析：
要使c₁f₁（x）＋c₂f₂（x）是方程y″＋p（x）y′＋q（x）y＝0的通解，则须满足f₁（x），f₂（x）线性无关，即ψ（x）＝f₁（x）/f₂（x）≠k（k为常数）。则ψ′（x）＝[f₁′（x）f₂（x）－f₁（x）f₂′（x）]/f₂²（x）≠0，即f₁′（x）f₂（x）－f₁（x）f₂′（x）≠0。
第21题：

判断题
若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.
A
对
B
错

正确答案：错
解析：暂无解析
第22题：

单选题
设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程（　　）的解。
A
y′＋P（x）y＝f₁（x）＋f₂（x）
B
y＋P（x）y′＝f₁（x）－f₂（x）
C
y＋P（x）y′＝f₁（x）＋f₂（x）
D
y′＋P（x）y＝f₁（x）－f₂（x）

正确答案： A
解析：
根据题意可知，y₁′＋P（x）y₁＝f₁（x），y₂′＋P（x）y₂＝f₂（x）。两式相加得（y₁′＋y₂′）＋P（x）（y₁＋y₂）＝f₁（x）＋f₂（x）。则可发现y＝y₁＋y₂是方程y′＋P（x）y＝f₁（x）＋f₂（x）的解。
第23题：

单选题
设f（x）在（－∞，＋∞）可导，x0≠0，（x0，f（x0））是y＝f（x）的拐点，则（　　）。
A
x₀必是f′（x）的驻点
B
（－x₀，－f（x₀））必是y＝－f（－x）的拐点
C
（－x₀，－f（x₀））必是y＝－f（x）的拐点
D
对∀x＞x₀与x＜x₀，y＝f（x）的凸凹性相反

正确答案： C
解析：
已知y＝f（x）与y＝－f（－x）的图像是关于原点对称的。那么由（x₀，f（x₀））是y＝f（x）的拐点，就能推出（－x₀，－f（x₀））是y＝－f（－x）的拐点。故选B项。

itgle.com

设f(x),f'(x)为已知的连续函数，则微分方程y'十f'(x)y=f(x)f'(x)的通解是： A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +c C. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)

题目

相似考题

参考答案和解析

更多“设f(x),f'(x)为已知的连续函数，则微分方程y'十f'(x)y=f(x)f'(x)的通解是： ”相关问题

相关内容