函数展开成(x-2)的幂级数是:
题目
函数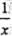 展开成(x-2)的幂级数是:
展开成(x-2)的幂级数是:
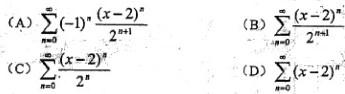
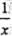 展开成(x-2)的幂级数是:
展开成(x-2)的幂级数是:
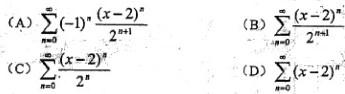
相似考题
更多“函数展开成(x-2)的幂级数是: ”相关问题
-
第1题:
函数y=x²+x-2,已知该曲线在点M处的切线斜率为3,则点M的坐标是(2,0)。()此题为判断题(对,错)。
参考答案:错误
-
第2题:
下列幂级数中,收敛半径R=3的幂级数是: 答案:D解析:
答案:D解析: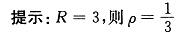
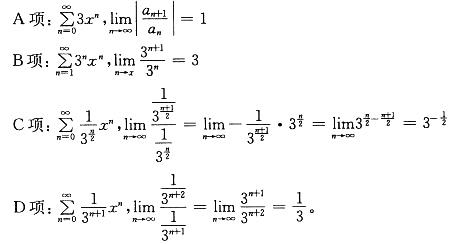
-
第3题:
函数ex展开成为x-1的幂函数是: 答案:B解析:提示:已知ex=e x- 1+1=e ? e x-1。
答案:B解析:提示:已知ex=e x- 1+1=e ? e x-1。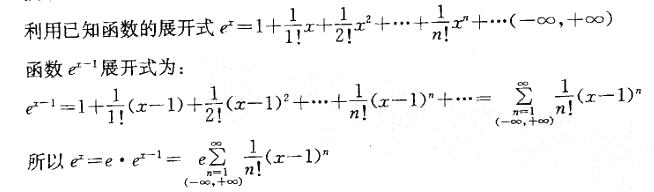
-
第4题:
求幂级数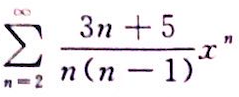 的收敛域与和函数.答案:解析:
的收敛域与和函数.答案:解析:
-
第5题:
将函数f(x)=1-x(0≤x≤π)展开成余弦级数,并求级数 的和.答案:解析:
的和.答案:解析:
-
第6题:
幂级数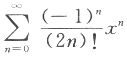 在(0,+∞)内的和函数S(x)=_________.答案:解析:利用余弦函数的幂级数展开式
在(0,+∞)内的和函数S(x)=_________.答案:解析:利用余弦函数的幂级数展开式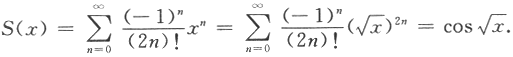
-
第7题:
当非正弦函数f(t)满足狄里赫利条件时,可将其展开成傅里叶级数。( )答案:对解析: -
第8题:
函数1/x展开成(x-2)的幂级数为( )。 答案:A解析:
答案:A解析: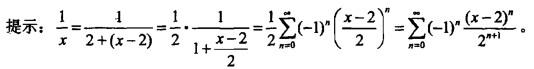
-
第9题:
将函数f(x)=xe3x展开为x的幂级数,并指出其收敛区间.答案:解析:
-
第10题:
如果遇到Z变换函数是超越函数,则只能用()来求取Z反变换。
- A、部分分式法
- B、反演积分法
- C、幂级数法
- D、延迟法
正确答案:B -
第11题:
设a<0,则当满足条件()时,函数f(x)=ax3+3ax2+8为增函数。
- A、x<-2
- B、-2
- C、x>0
- D、x<-2或x>0
正确答案:B -
第12题:
单选题在1912年芬兰的Sundman找到了关于三体问题的什么形式的解()?A代数函数
B幂级数
C定积分
D常微分
正确答案: B解析: 暂无解析 -
第13题:
Scala函数组合器可以把一个二维的列表展开成一个一维的列表的方法是()。正确答案:flatten
-
第14题:
幂级数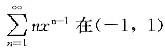 内的和函数为( )。
内的和函数为( )。 答案:B解析:设
答案:B解析:设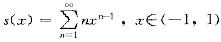 由逐项积分
由逐项积分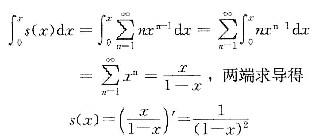
-
第15题:
函数1/x展开成(x-2)的幂级数是: 答案:A解析:提示:将函数1/x变形后,再利用已知函数1/(x+1)的展开式写出结果。
答案:A解析:提示:将函数1/x变形后,再利用已知函数1/(x+1)的展开式写出结果。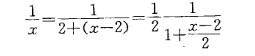
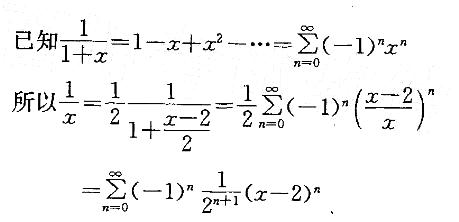
-
第16题:
幂级数 在区间(-1,1)内的和函数S(x)=________.答案:解析:
在区间(-1,1)内的和函数S(x)=________.答案:解析: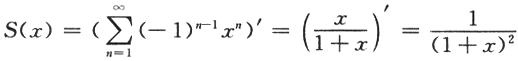
-
第17题:
设数列{an}满足条件:a0=3,a1=1,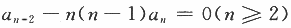 ,S(x)是幂级数
,S(x)是幂级数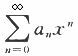 的和函数.
的和函数.
(Ⅰ)证明:S"(x)-S(x)=0;
(Ⅱ)求S(x)的表达式.答案:解析:【分析】利用幂级数可逐项求导的性质,验证(Ⅰ)成立;解微分方程求出S(x),注意初值条件的使用.

-
第18题:
函数1/x展开成(x-2)的幂级数是( )。A.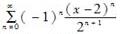
B.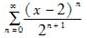
C.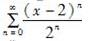
D.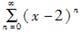 答案:A解析:
答案:A解析: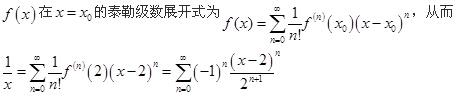
-
第19题:
当∣x∣≤4时,函数y=∣x-1∣+∣x-2∣+∣x-3∣的最大值与最小值之差是A.4
B.6
C.16
D.20
E.14答案:C解析:
-
第20题:
幂级数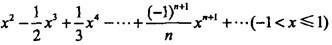 的和是( )。
的和是( )。
 答案:C解析:
答案:C解析: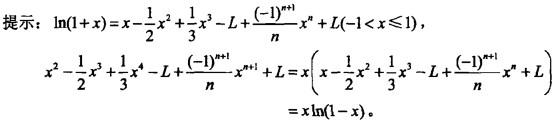
-
第21题:
在电工技术中所遇到的周期函数一般都可以展开成一个()级数。
正确答案:傅里叶 -
第22题:
MATLAB中提供的将函数展开为幂级数的函数是()。
- A、taylor
- B、expand
- C、symsum
- D、float
正确答案:A -
第23题:
填空题由于高斯投影是按带投影的,在各投影带内()不大,()是一微小量。故可将函数x=x(l,q),y=y(l,q)展开为()的幂级数。正确答案: 经差l,l/p,经差l解析: 暂无解析
