itgle.com

函数在[1，2]上符合拉格朗日定理条件的ζ值为：

题目
函数在[1，2]上符合拉格朗日定理条件的ζ值为：

相似考题

1.“孙子定理”和拉格朗日插值公式在思想方法上是相通的。()此题为判断题(对，错)。

2.根据拉格朗日余项定理，当n=0时，可以推出中值定理。()

3.差商形式插值公式称为()A、牛顿插值公式B、拉格朗日插值公式C、分段插值公式D、埃尔米特插值公式

4.拉格朗日插值法和牛顿插值法的共同缺点是:插值曲线在节点处不光滑、有尖点,而且插值多项式在节点处不可导。()

更多“函数在[1，2]上符合拉格朗日定理条件的ζ值为： ”相关问题

  • 第1题：

    所谓()插值，就是将被插值函数逐段多项式化。

    A、牛顿

    B、拉格朗日

    C、三次样条

    D、分段


    参考答案：D

  • 第2题：

    区间估计和点估计的理论其核心分别是()。

    A、中心极限定理

    B、大数定理

    C、柯西中值定理

    D、拉格朗日定理


    答案:A

    解析:
    中心极限定理是推断统计（包含参数估计和假设检验）的理论基础，从而也是参数估计（包含点估计和区间估计）的核心。

  • 第3题：

    对于定常流动,在( )表达式中流动参数与时间变量无关。

    A.欧拉

    B.拉格朗日

    C.欧拉和拉格朗日


    参考答案A

  • 第4题：

    一元函数的插值方法有()

    A、线性插值法

    B、拉格朗日插值法

    C、最小二乘法

    D、指数函数法


    参考答案：AB

  • 第5题：

    叙述并证明拉格朗日微分中值定理,并简述拉格朗日中值定理与中学数学内容的联系。


    答案：
    解析：

  • 第6题：

    研究流体运动的两种方法应该是（）。

    • A、拉格朗日法和欧拉法均以质点为研究对象
    • B、拉格朗日法和欧拉法均以固定空间为研究对象
    • C、拉格朗日法以质点为研究对象，而欧拉法以固定空间为研究对象
    • D、拉格朗日法以固定空间为研究对象，而欧拉法以质点为研究对象

    正确答案:C

  • 第7题：

    一般处理有条件极值问题用的方法是（）。

    • A、将条件代入目标函数求解法
    • B、化为一元函数无条件极值处理
    • C、拉格朗日乘数法
    • D、最小二乘法

    正确答案:C

  • 第8题：

    使用波函数描述电子运动状态的方程是（）

    • A、牛顿方程
    • B、拉格朗日运动方程
    • C、薛定谔方程
    • D、伯努利方程

    正确答案:C

  • 第9题：

    下列哪个定理与沟通无关（）

    • A、斯坦纳定理
    • B、拉格朗日定理
    • C、费斯诺定理
    • D、避雷针效应

    正确答案:B

  • 第10题：

    单选题
    研究流体运动的两种方法应该是（）。
    A

    拉格朗日法和欧拉法均以质点为研究对象

    B

    拉格朗日法和欧拉法均以固定空间为研究对象

    C

    拉格朗日法以质点为研究对象，而欧拉法以固定空间为研究对象

    D

    拉格朗日法以固定空间为研究对象，而欧拉法以质点为研究对象


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    一般处理有条件极值问题用的方法是（）。
    A

    将条件代入目标函数求解法

    B

    化为一元函数无条件极值处理

    C

    拉格朗日乘数法

    D

    最小二乘法


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    下列哪个定理与沟通无关（）
    A

    斯坦纳定理

    B

    拉格朗日定理

    C

    费斯诺定理

    D

    避雷针效应


    正确答案： B
    解析： 暂无解析

  • 第13题：

    为了保证插值函数能更好地密合原来的函数，不但要求“过点”，即两者在节点上具有相同的函数值，而且要求“相切”，即在节点上还具有相同的导数值，这类插值称为()

    A、牛顿插值

    B、埃尔米特插值

    C、分段插值

    D、拉格朗日插值


    参考答案：B

  • 第14题：

    Simpson公式的计算思想是以2次()多项式近似代替被积函数做积分。

    A、牛顿插值

    B、拉格朗日插值

    C、LegendrE

    D、泰勒


    参考答案：B

  • 第15题：

    对定常湍流,相关矩和谱函数之间互为___变换。

    A、欧拉

    B、泰勒

    C、拉格朗日

    D、傅里叶


    参考答案：D

  • 第16题：

    下列函数在区间[0，3]上不满足拉格朗日定理条件的是（ ）《》（ ）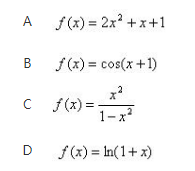


    答案：C
    解析：

  • 第17题：

    叙述并证明拉格朗日微分中值定理，并简述拉格朗日微分中值定理与中学数学内容的联系。


    答案：
    解析：
    本题主要考查微分中值定理中十分重要的拉格朗日中值定理。

    证明拉格朗日微分中值定理，首先要从罗尔定理出发，

  • 第18题：

    对于具有外力作用的非保守机械系统，其拉格朗日动力函数L可定义为系统总动能与系统总势能之和。


    正确答案:错误

  • 第19题：

    拉格朗日在《解析函数论》一书中，主张用（）来定义导数，以此作为整个微分、积分演算的出发点而将微积分归结为“代数运算”。


    正确答案:拉格朗日定理

  • 第20题：

    下列不属于函数插值法的是（）

    • A、线性插值
    • B、抛物线插值
    • C、拉格朗日插值
    • D、多次插值

    正确答案:D

  • 第21题：

    拉格朗日法


    正确答案:通过描述每一质点的运动达到了解流体运动的方法称为拉格朗日法。

  • 第22题：

    单选题
    “幂级数的求导和积分可以逐项进行，可以用来近似计算函数的值”，这都要归功于：（）。
    A

    拉格朗日

    B

    祖冲之

    C

    极限

    D

    泰勒公式


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    下列不属于函数插值法的是（）
    A

    线性插值

    B

    抛物线插值

    C

    拉格朗日插值

    D

    多次插值


    正确答案： B
    解析： 暂无解析

相关内容