itgle.com

图示梁的抗弯刚度为EI，长度为l，欲使梁中点C弯矩为零，则弹性支座刚度k的取值应为（　　）。

题目
图示梁的抗弯刚度为EI，长度为l，欲使梁中点C弯矩为零，则弹性支座刚度k的取值应为（　　）。



相似考题

1.钢筋棍凝土梁的抗弯刚度为一随弯矩增大而减小的变量。()

2.已知图示两梁的抗弯截面刚度EI相同，若两者自由端的挠度相等，则P1/P2为: A.2 B.4 C.8 D.16

3.已知图示梁抗弯刚度EI为常数，则用叠加法可得跨中点C的挠度为：

4.有如图所示简支梁，其抗弯刚度EI为常数。该梁的挠曲线方程为()。A.B.C.D.

更多“图示梁的抗弯刚度为EI，长度为l，欲使梁中点C弯矩为零，则弹性支座刚度k的取值应为（　　）。 ”相关问题

  • 第1题：

    已知图示梁抗弯刚度EI为常数，则用叠加法可得自由端C点的挠度为：



    答案：D
    解析：
    提示：为了查表方便，先求整个梁布满向下均布荷载时C点的挠度，再减去AB段承受向上均布荷载时C点的挠度。

  • 第2题：

    在图示体系中，集中质量为m，杆长为l，抗弯刚度为EI，杆重不计。该体系自由振动的周期为（　　）。



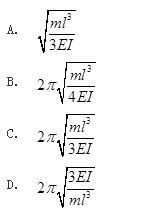    答案：C
    解析：

  • 第3题：

    已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：




    答案：C
    解析：
    提示：使用BA杆的转角位移方程。

  • 第4题：

    图示组合结构，梁AB的抗弯刚度为EI，二力杆的抗拉刚度都为EA。DG杆的轴力为（　　）。


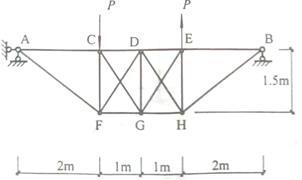    A、0
    B、P，受拉
    C、P，受压
    D、2P，受拉

    答案：A
    解析：
    该题是对称结构作用反对称荷载，对称轴处只有反对称的内力，没有正对称的内力。故DG杆的轴力为正对称的力所以DG杆的轴力为零。

  • 第5题：

    图示结构B处弹性支座的弹性刚度k＝3EI/l3，B结点向下的竖向位移为（　　）

    A．Pl3/（12EI）
    B．Pl3/（6EI）
    C．Pl3/（4EI）
    D．Pl3/（3EI）

    答案：B
    解析：
    撤去B支座约束，代以未知反力X，方向向上，得到力法的基本体系，则有力法方程δ11X1＋Δ1P＝－X1/k。做出集中荷载单独作用下基本体系的弯矩图，如题45解图（a）所示。在B端作用一个方向向上的单位力，并做出弯矩图，如题45解图（b）所示。由图乘法：

  • 第6题：

    图示结构，EI为常数。结点B处弹性支撑刚度系数k=3EI/L3，C点的竖向位移为（　　）。




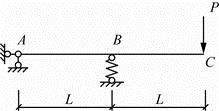
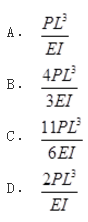    答案：D
    解析：

  • 第7题：

    图示梁的抗弯刚度为EI，长度为l，k＝6EI/l3，跨中C截面弯矩为（以下侧受拉为正）（　　）。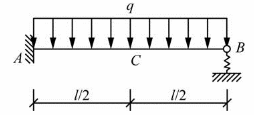

    A．0
    B．ql2/32
    C．ql2/48
    D．ql2/64

    答案：A
    解析：
    撤去支座B约束，代以未知反力X，方向向上，得到力法的基本体系，则有力法方程δ11X1＋Δ1P＝－X1/k。作出均布荷载单独作用下基本体系的弯矩图，如题42解图（a）所示。在B端作用一个方向向上的单位力，并做出弯矩图，如题42解图（b）所示。由图乘法：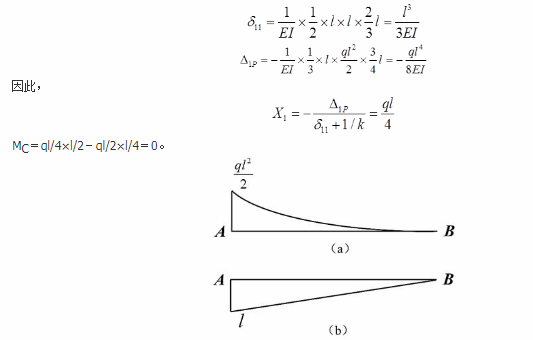

  • 第8题：

    图示梁的抗弯刚度为EI，长度为l，欲使梁中点C弯矩为零，则弹性支座刚度k的取值应为（　　）




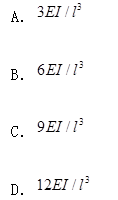    答案：B
    解析：
    知识点:利用力法对超静定结构的内力求解；

  • 第9题：

    图示结构当水平支杆产生单位位移时（未注的杆件抗弯刚度为EI），B-B截面的弯矩值为（　　）。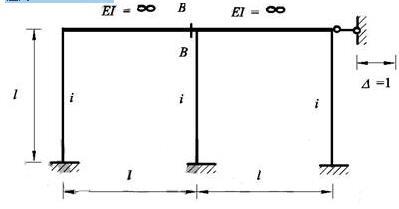



    答案：C
    解析：
    由题39图可知，在计算B-B截面的弯矩时，先把B点看成一个固定端。则可把B到最右端看成是一个一端铰接一端固定的直杆。再根据表1可得B端的弯矩为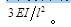

    表1　等截面直杆的固端弯矩和固端剪力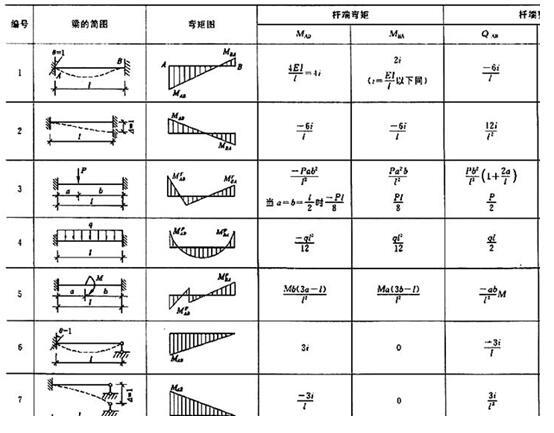

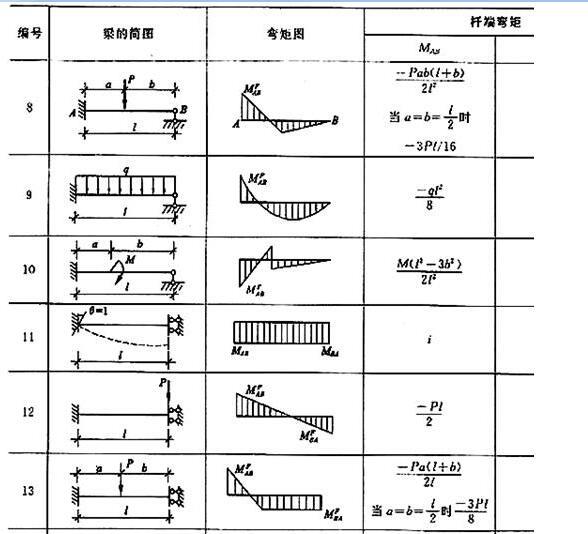
  • 第10题：

    已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2为：

    A.2
    B. 4
    C. 8
    D. 16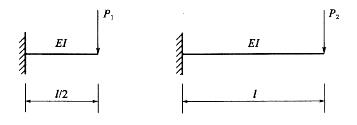


    答案：C
    解析：

  • 第11题：

    验算钢筋混凝土梁的挠度时，采用的弯矩值是按荷载（）组合计算的最大弯矩，梁的抗弯刚度采用（）刚度。


    正确答案:短期效应；长期

  • 第12题：

    在梁的弯曲正应力的计算公式中，EI表示（）

    • A、抗扭刚度
    • B、抗压刚度
    • C、抗弯刚度
    • D、抗拉刚度

    正确答案:C

  • 第13题：

    已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2为：
    A.2 B. 4 C. 8 D. 16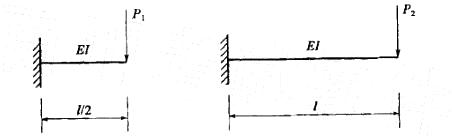


    答案：C
    解析：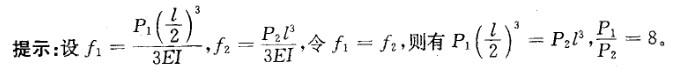

  • 第14题：

    如图所示结构，集中质量m在刚性梁的中点，EI=∞，弹簧刚度为k，该体系自振频率为（　　）。




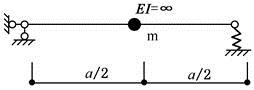
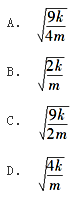    答案：D
    解析：

  • 第15题：

    图示结构，质量m在杆件中点，EI＝∞，弹簧刚度为k，该体系自振频率为（　　）。




    答案：D
    解析：
    知识点:单自由度体系的自振频率求解；

  • 第16题：

    图示连续梁，EI=常数，欲使支承B处梁截面的转角为零，比值a/b应为：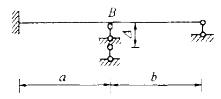


    答案：D
    解析：
    提示：由Δ引起的B两边固端弯矩绝对值相等。

  • 第17题：

    图示梁线刚度为i，长度为ι，当A端发微小转角α，B端发生微小位△ια时，梁两端弯矩（对杆端顺时针为正）为（　　）。




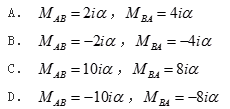    答案：B
    解析：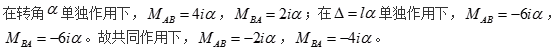

  • 第18题：

    图示为刚架在均布荷载作用下的M图，曲线为二次抛物线，横梁的抗弯刚度为2EI，竖柱为EI，支座A处截面转角为：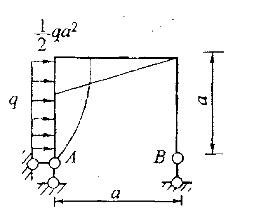



    答案：A
    解析：
    提示：应用图乘法。

  • 第19题：

    图示结构B处弹性支座的弹簧刚度k＝12EI/l3，B截面的弯矩为（　　）。


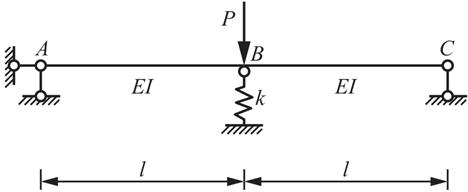    A． Pl/2
    B． Pl/3
    C． Pl/4
    D． Pl/6

    答案：D
    解析：
    利用力法求解，取基本结构，断开B处支座，反力以X1代替。在B处施加向下的单位力，分别作出荷载作用下与单位力作用下基本结构的弯矩，并进行图乘，可求得δ11＝l^3/（6EI），Δ1P＝Pl^3/（6EI），列出力法的基本方程：X1δ11＋Δ1P＝－X1/k，解得X1＝－2P/3。将荷载作用下与单位力作用下的弯矩图叠加，可求得原结构B截面弯矩：MB＝MBP＋MB1×X1＝Pl/2－（l/2）×（2P/3）＝Pl/6（下侧受拉）。

  • 第20题：

    图示连续梁，EI=常数，欲使支承B处梁截面的转角为零，比值a/b应为：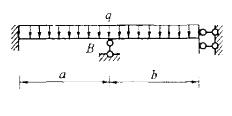


    A. 1/2
    B. 2
    C. 1/4
    D. 4

    答案：B
    解析：
    提示：当B截面转角为零时，相应有固端弯矩而达平衡状态，B两边固端弯矩绝对值相等。

  • 第21题：

    图示结构，集中质量m在刚性梁的中点，EI=∞，弹簧刚度为k，该体系自振频率为（　　）。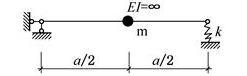



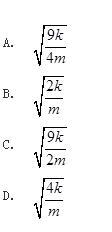    答案：D
    解析：

  • 第22题：

    图示结构连续梁的刚度为EI，梁的变形形式为( )。

    A.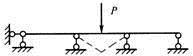
    B.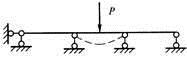
    C.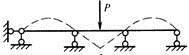
    D.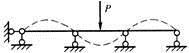

    答案：D
    解析：
    图示结构为连续梁，当中间一跨受力产生向下变形时，要带动左右两跨产生向上的变形，而且应是一条连续光滑的挠度曲线，变形的曲线没有突变。

  • 第23题：

    梁的挠曲线近似微分方程确立了梁的挠度的（）与弯矩、抗弯刚度之间的关系。梁弯曲时，如果梁的抗弯刚度愈大，则梁的曲率愈（），说明梁愈不容易变形。


    正确答案:二阶导数；小

  • 第24题：

    梁在弯曲变形时，其中性层的曲率（）

    • A、与弯矩成反比，与抗弯刚度成正比
    • B、与弯矩成正比，与抗弯刚度成反比
    • C、与弯矩及抗弯刚度均成正比
    • D、与弯矩及抗弯刚度均成反比

    正确答案:B

相关内容