itgle.com

任意抛掷三枚硬币，恰有两枚正面朝上的概率为（).A．3/4B．3/8C．1/3D．1/4

题目

任意抛掷三枚硬币，恰有两枚正面朝上的概率为（).

A．3/4

B．3/8

C．1/3

D．1/4

相似考题

1.同时抛掷3枚均匀的硬币，则恰好有两枚正面朝上的概率为（ ）A．0.125 B．0.25C．0.375 D．0.50

2.一枚均匀硬币连续抛掷3次，求3次均在正面向上的概率

3.小明和小芳做抛硬币的游戏（硬币是均匀的）。（1）小明前三次抛的结果都是正面朝上，第四次一定会是正面朝上吗？（2） 小芳抛10次硬币，一定是5次正面朝上、5次反面朝上吗？你怎么看以上两个问题，与同伴交流。

4.投掷两枚硬币，其样本空间是( )。A．Ω={正面，反面}B．Ω={(正面，反面)，(反面，正面)}C．Ω={(正面，正面)，(正面，反面)，(反面，正面)，(反面，反面)}D．Ω={(正面，正面)，(反面，反面)}

更多“任意抛掷三枚硬币，恰有两枚正面朝上的概率为（).”相关问题

  • 第1题：

    同时抛掷3枚均匀的硬币，则恰好有两枚正面向上的概率为

    A、0.5

    B、0.25

    C、0.125

    D、0.375


    正确答案:D

  • 第2题：

    根据概率论，抛掷一枚均匀的硬币，其正面朝上和反面朝上的概率几乎相等。我与人打赌，若抛掷硬币正面朝上，我赢；若反面朝上，我输。我抛掷硬币6次，结果都是反面朝上，已经连输了6次。因此，我后面的几次抛掷肯定是正面朝上，一定会赢回来。

    下面哪一个选项是对“我”的推理的恰当评价？

    A．有道理，因为上帝是公平的，几乎是均等的，他不回总倒霉。

    B．没道理，因为每一次抛掷都是独立事件，与前面的结果没有关系。

    C．后面几次抛掷果然大多正面朝上，这表明概率论是正确的。

    D．这只是他个人的信念，无法进行理性的或逻辑的评价。


    正确答案：B

  • 第3题：

    同时抛掷3枚均匀的硬币，恰好有两枚正面向上的概率为（）。

    A.1/4

    B.3/8

    C.1/2

    D.1/3


    正确答案：B

  • 第4题：

    同时抛掷两枚1元的硬币，正面都朝上的概率是()。

    A.1/2
    B.1/3
    C.1/4
    D.1/5

    答案：C
    解析：

  • 第5题：

    如下事件发生的概率等于1/4的是()。

    A:抛两枚普通的硬币，出现的均是正面
    B:一个不透明的袋子里装着黑白红蓝四种颜色的球，随机拿出一个恰好为红色球
    C:抛两枚普通的硬币，出现一个正面和一个反面
    D:掷一枚普通的骰子，出现点数小于3
    E:掷两枚普通的骰子，出现点数之和小于

    答案：A,B
    解析：
    A选项，出现两个都是正面的概率=1/2*1/2=1/4；B选项，考查古典概率计算方法的使用，随机拿出一个球可能有4种颜色，红色只占其中一种，所以拿出恰为红色球的概率=1/4；C选项，出现一个正面和一个反面应该包括两种情况：正反、反正，因此其概率=1/4+1/4=1/2；D选项，掷出的点数总共有6种情况，而小于3的只有l和2两种情况，所以其概率=2/6=1/3；E选项，掷两枚骰子，出现的点数和最小为2，即两枚骰子的点数都是1，因此其和小于2是不可能事件，所以概率=0。

  • 第6题：

    任意抛掷一枚硬币两次，落地后正面的次数可能为（ ）

    A：1次
    B：2次
    C：3次
    D：4次

    答案：A,B
    解析：

  • 第7题：

    同时抛掷三枚均匀的硬币，正面与反面都出现的概率为( )。

    A、1/4
    B、1/3
    C、2/3
    D、3/4

    答案：D
    解析：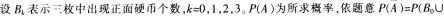

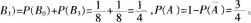
  • 第8题：

    抛两枚硬币，一枚朝上一枚朝下的概率是（）

    • A、10%
    • B、25%
    • C、75%
    • D、100%

    正确答案:B

  • 第9题：

    晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为。（）

    • A、1/2
    • B、1/11
    • C、1/7
    • D、1/18。

    正确答案:A

  • 第10题：

    抛掷一枚均匀的硬币，出现正面的概率是（）。

    • A、0
    • B、1
    • C、0.5
    • D、0.8

    正确答案:C

  • 第11题：

    问答题
    现在桌子上面放了25枚硬币，其中有10枚硬币是正面朝上。如果别人蒙住你的眼睛，而且你的手也摸不出硬币的反正面。你用什么方法能将硬币分成两堆，而且这两堆硬币正面朝上的个数相同？

    正确答案： 查15个硬币放在一堆，再查10个硬币放在一堆。然后将10个硬币全部翻面就行了，其实就是取补数。
    解析： 暂无解析

  • 第12题：

    单选题
    投掷两枚硬币，其样本空间是（　　）。
    A

    Ω＝{正面，反面}

    B

    Ω＝{（正面，反面），（反面，正面）}

    C

    Ω＝{（正面，正面），（正面，反面），（反面，正面），（反面，反面）}

    D

    Ω＝{（正面，正面），（反面，反面）}


    正确答案： B
    解析： 每个硬币可能出现的情况为:正面，反面，故“投掷两枚硬币”的样本空间为:Ω＝{（正面，正面），（正面，反面），（反面，正面），（反面，反面）}。

  • 第13题：

    （2）连续4次抛掷一枚硬币，求恰出现两次是正面的概率和最后两次出现是正面的概率。


    正确答案：
              

  • 第14题：

    将3枚均匀的硬币各抛掷一次，恰有2枚正面朝上的概率为 （ ）

    A.A

    B.B

    C.C

    D.D


    正确答案：C
    本题主要考查的知识点为随机事件的概率．【应试指导】

  • 第15题：

    根据概率论，抛出一枚均匀的硬币，其正面朝上和反面朝上的概率几乎相等。我与人打赌，若抛出硬币正面朝上，我赢：若反面朝上，我输。我抛出硬币6次。结果都是反面朝上，已经连输6次。因此，我后面的几次抛出肯定是正面朝上，一定会赢回来。下面哪一个选项是对“我”的推理的恰当评价?

    A．有道理，因为上帝是公平的，机会是均等的，他不会总倒霉。

    B．没道理。因为每一次抛出都是独立事件，与前面的结果没有关系。

    C．后面几次抛出果然大多正面朝上，这表明概率论是正确的。

    D．这只是他个人的信念，无法进行理性的或逻辑的评价。


    正确答案：B
    解析：本题不是一道真正意义上的逻辑题，实际上考察的是对概率问题的正确理解，B项是对题干推理的恰当评价。

  • 第16题：

    关于频率与概率有下列几种说法
    ①“明天下雨的概率是90％”，表示明天下雨的可能性很大
    ②“抛一枚硬币正面朝上的概率为50％”，表示每抛两次硬币就有一次正面朝上
    ③“某彩票中奖的概率是1％”，表示买10张该种彩票不可能中奖
    ④“抛一枚硬币正面朝上的概率为50％”，表示随着抛掷硬币次数的增加，“抛出正面朝上”这一事件发生的频率稳定在50％附近
    其中正确的说法是()。

    A.①④
    B.②③
    C.④
    D.①③

    答案：A
    解析：
    事件A的概率P(A)是对事件A发生可能性大小的一个度量，它是一个确定的数值，与试

  • 第17题：

    任意抛掷一枚硬币两次，落地后为正面次数可能为( )

    A. 1 次
    B.2 次
    C. 3次
    D. 0次

    答案：A,B,D
    解析：

  • 第18题：

    同时抛掷三枚质地完全相同的硬币，则正面与反面都出现的概率为（ ）。

    A.1/4
    B.1/3
    C.2/3
    D.3/4

    答案：D
    解析：

  • 第19题：

    抛掷一枚硬币，正面朝上还是反面朝上，这一现象符合正态分布。


    正确答案:错误

  • 第20题：

    抛两枚硬币，两枚都是朝上的概率是（）

    • A、10%
    • B、25%
    • C、75%
    • D、100%

    正确答案:B

  • 第21题：

    同时掷3枚均匀硬币，则恰有2枚正面朝上的概率为（）.

    • A、0.5
    • B、0.25
    • C、0.125
    • D、0.375

    正确答案:D

  • 第22题：

    随机投掷一枚硬币，则两次都正面朝上的概率是（）。

    • A、1/4
    • B、1/2
    • C、3/4
    • D、1

    正确答案:A

  • 第23题：

    单选题
    抛两枚硬币，两枚都是朝上的概率是（）
    A

    10%

    B

    25%

    C

    75%

    D

    100%


    正确答案： A
    解析： 暂无解析

  • 第24题：

    单选题
    抛两枚硬币，一枚朝上一枚朝下的概率是（）
    A

    10%

    B

    25%

    C

    75%

    D

    100%


    正确答案： C
    解析： 暂无解析

相关内容