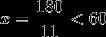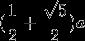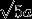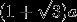itgle.com

数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。 小明有48支铅笔．小刚有36支铅笔。若每次小明给小刚8支，同时小刚又还给小明4支，问经过这样的交换，几次后小刚的铅笔数是小明的2倍?（） A.7 B.5 C.4 D.2

题目
数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
小明有48支铅笔．小刚有36支铅笔。若每次小明给小刚8支，同时小刚又还给小明4支，问经过这样的交换，几次后小刚的铅笔数是小明的2倍?（）
A.7
B.5
C.4
D.2

相似考题

1.二、数学运算。在这部分试题中，每道试题呈现一段表述数宇关系的文字，要求你迅速，准确地计算出答案。你可以在草稿纸上运算。请开始答题：计算：173+183+193+203+…+263=（ ）。A. 104705B. 116704C. 105029D. 118027

2.数学运算。在这部分试题中。每道试题给出一段表述数字关系的文字，要求你迅速、准确地计算出答案。请开始答题：若将241×(△+7)错看成241×△+7进行计算，得到的结果比正确答案少( )。A．1860B．880C．1680D．1080

3.二、数学运算：共10题。在这部分试题中，每道试题呈现一道算术式。或是表述数字关系的一段文字。要求你迅速、准确地计算出答案。你可以在草稿纸上运算。请开始答题：51．3×999+8×99+4×9+15的值是( )。A．3866B．3855C．3840D．3877

4.数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。你．你可以在草稿纸上运算。请开始答题：(8.4×2.5+9.7)÷(1.05÷1.5+8.4÷0.28)的值为( )。A．1B．1.5C．2D．2.5

更多“数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。 ”相关问题

  • 第1题：

    二，数学运算。在这部分试题中，每道试题陈述一段表述数字关系的文字，要求你迅速准确的计算出答案。

    第46题：（1/31）+（202/3131）+（50505/313131）+(13131313/31313131)

    A.20/30 B.21/31

    C.22/31 D.23/31


    正确答案：B

  • 第2题：

    数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字。要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    请开始答题：

    2004×(2.3×47+2.4)÷(2.4×47-2.3)=?

    A．2003

    B．2004．

    C．2005

    D．2006


    正确答案：B
    [答案] B。[解析] 2.3×47+2.4=2.4×47-0.1×47+2.4=2.4×47-2.3，所以原式=2004×(2.4×47-2.3)÷(2.4×47-2.3)=2004。

  • 第3题：

    数学运算。在这个部分试题中，每道试题呈现一段表述数学关系的文字，要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    计算：(2+4+6+8+…+2010)-(1+3+5+7+…+2009)=( )。

    A．995

    B．1011

    C．1111

    D．1005


    正确答案：D
    D[解析]原式=(2-1)+(4-3)+(6-5)+(8-7)+…+(2010-2009)
    =1+1+1+1+…+1
    从2到2010共有1005个偶数，所以原式等于1005个1相加，等于1005，故本题答案为D。

  • 第4题：

    数学运算。每道试题呈现一段表述数学关系的文字，要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    请开始答题：

    计算：3262+741-1092=( )。

    A．95082

    B．95136

    C．96348

    D．96647


    正确答案：B
    B[解析]本题用尾数估算法可以快速选出答案。326的平方尾数为6，与741相加后尾数为7，109的平方尾数为1，因此最终结果的尾数应为6，符合这一要求的只有B项。

  • 第5题：

    二、数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字，要求考生迅速、准确地计算出答案。

    41. 20082008+20092009的个位数是()。

    A. 3

    B. 5

    C. 7

    D. 9


    正确答案：B

  • 第6题：

    二、数学运算在这部分试题中，每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    46.11338×25593的值为 （ ）

    A.290133434

    B.290173434

    C.290163434

    D.290153434


  • 第7题：

    二、数学运算o在这部分试题中，每道试题呈现一段表述数字关系的文字，要求你迅速准确地计算出答案，你可以在草稿纸上运算。

    请开始答题：

    91.由0、2、3、4这四个数组成的年份中，在21世纪的有多少个？

    A．9

    B．16

    C．15

    D.27


    正确答案：C
    年份的前两位可以确定分别为2、0，后两位有4x4=16种不同选择，2000年属于20世纪，因此共有16-1=15个。

  • 第8题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    5586876×52145846的后两位数字之和是（）。
    A.13
    B.14
    C.15
    D.16


    答案：C
    解析：
    可用尾数法计算。题干要求计算结果的后两位数字之和，只需算出76×46=3496，其后两位数字之和为9+6=15．即为所求，故选择C。

  • 第9题：

    数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字．要求你迅速、准确地计算出答案。
    四名学生和两位老师站一排照相．两老师不在两头但相邻的排法有（）种。
    A.72
    B.108
    C.144
    D.288


    答案：C
    解析：
    方法一：
    第一步，把两个老师看成一个整体，即一个人。这样相当于只有5个人排队。由于老师不能排在两端．所以应该从中间的三个位置中选一个位置给老师排．而两个老师之间可以互换，所以这样两个老师共有种不同的排法；第二步：排学生，剩余四个位置四个学生排，共有种排法。所以一共有6×=144种不同的排法。
    方法二：用间接法
    老师相邻的全部排法有：；老师排在两端的排法有：4×=96；所以，一共有240-96=144种不同的排法。

  • 第10题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    下图是一块长方形铁皮，利用图中的阴影部分铁皮，刚好能做成一个带盖的铁桶．请问该铁桶的容积为多少毫升?(π取3．14)（）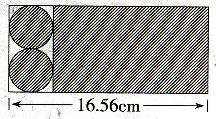

    A.12．56
    B.50.24
    C.94．2
    D.100．48


    答案：D
    解析：
    设铁桶底面半径为只，则图中阴影部分长方形的长为底面周长2πR，宽为铁桶的高4R，则2R+2πR=16．56cm，R=2cm。铁桶的容积为毫升。

  • 第11题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    从12时到13时，钟的时针与分针可成直角的机会有（）。
    A.1次
    B.2次
    C.3次
    D.4次


    答案：B
    解析：
    设过了x(x第一种情况：分针比时针多走90°，5．5x=90，解之得：
    第二种情况：分针比时针多走270°,5．5x=270，解之得：
    总共有两次。选择B。

  • 第12题：

    数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字．要求你迅速、准确地计算出答案。
    某戏院一共卖了1200张票．其中前排票每张40元，后排票每张50元。已知后排比前排多卖了16800元。问前排票卖出了多少张?（）
    A.480
    B.560
    C.640
    D.720


    答案：A
    解析：
    假设全部都是后排票，则后排要比前排多卖50×1200=60000元。
    每多卖出一张前排票．两者的差距就减少50+40=90元。
    因此．前排票卖出了(60000—16800)÷90=480张。

  • 第13题：

    数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    请开始答题：

    一个三位数能分别被10、12、18除尽，那么这个三位数的各位数字之和为多少?

    A．14

    B．15

    C．12

    D．9


    正确答案：D
    [答案] D[解析]此数能被18整除，即也能被9整除，所以各位数字之和应能被9整除，选项中只有D符合。

  • 第14题：

    数学运算。在这个部分试题中。每道试题呈现一段表述数学关系的文字。要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    请开始答题：

    计算：66+666+6666+…+66666666=( )。

    A．74073092

    B．74074062

    C．74073396

    D．74007396


    正确答案：B
    B[解析]原式=6×(1+11+111+1111+…+11111111)-6
    =6×12345678-6
    =74074068-6
    =74074062
    由此可知本题正确答案为B。

  • 第15题：

    数学运算。在这个部分试题中，每道试题呈现一段表述数学关系的文字。要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    请开始答题：

    若将241×(△+7)错看成241×△+7进行计算，得到的结果比正确答案少( )。

    A．1860

    B．880

    C．1680

    D．1080


    正确答案：C
    C [解析] 241×(+7)=241×+241×7，比241×+7多了240个7，即240×7=1680。所以本题正确答案应该为C。

  • 第16题：

    二、数学运算，共 7 题。在这部分试题中，每道题呈现一道算术式，或是表述数字关系的一段文字，要求你迅速、准确地计算出答案。

    9、16 支球队分两组，每组打单循环赛，共需打（ ）场比赛。

    A.16

    B.56

    C.64

    D.120


    正确答案：B
    9.B【解析】16 支球队平均分两组，每组打单循环赛，共需打（7+6+5+4+3+2+1）×2=56 （场）或 C28×2=8×72×2=56(场)比赛。故选 B。

  • 第17题：

    二、数学运算（在这部分试题中，每道试题呈现一段表述数字关系的文字或图形，要求你迅速、准确地计算或论证出答案）

    第 46 题 11338×25593的值为：

    A．290133434

    B．290173434

    C．290163434

    D．290153434


    正确答案：B

  • 第18题：

    请教:09年江苏公务员行测模拟试题及答案详解(1)第2大题第6小题如何解答?

    【题目描述】

    数学运算

    在这部分试题中。每道试题呈现一段表述数字关系的文字。要求你迅速、准确地计算出答案。你可以在草稿纸上运算。

    第46题：58，74，62，3，（　　）。

    A．210

    B．220

    C．230

    D．240

     


    正确答案：A

  • 第19题：

    二、数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字．要求你迅速准确地计算出答案，你可以在草稿纸上运算。

    请开始答题：

    91.如果aOb表示(a-2)xb，那么当(aO2)03=12时，口等于多少？

    A．3

    B．4

    C．5

    D．6


    正确答案：C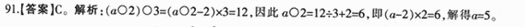

  • 第20题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    有五个连续偶数，已知第三个数比第一个数与第五个数之和的多18，则这五个偶数之和是（）。
    A.210
    B.180
    C.150
    D.100


    答案：B
    解析：
    设第一个数为x，由题意列方程：x+4=×(2x+8)+18，解得x=32。五个偶数之和为(32+32+8)×5÷2=180，选择B。

  • 第21题：

    数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字．要求你迅速、准确地计算出答案。
    2001年3月1日星期三．那么2003年5月1日是星期几?（）
    A.星期二
    B.星期三
    C.星期四
    D.星期五


    答案：B
    解析：
    因为2001年至2003年经过两年都是平年，所以2003年3月1日是星期五(同一日期过一平年星期加一)。2003年3月1日到5月1日共31+30=61天，61÷7=8……5，星期五再加5天是星期三．所以2003年5月1日是星期三。

  • 第22题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    计算1991×199219921992-1992×199119911991的值是（）。
    A.10
    B.1
    C.0
    D.-1


    答案：C
    解析：
    1991×199219921992-1992×199119911991=1991×1992×(100010001-100010001)=0，所以选择C。

  • 第23题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    一只蚂蚁从图的正方体A顶点沿正方体的表面爬到正方体C顶点。设正方体边长为a，问该蚂蚁爬过的最短路程为（）。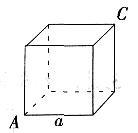

    A.
    B.
    C.
    D.


    答案：B
    解析：
    根据两点之间线段最短，将正方体展开为平面。根据勾股定理A到C的直线距离为。

  • 第24题：

    数学运算。在这部分试题中，每道试题呈现一段表述数字关系的文字．要求你迅速、准确地计算出答案。
    64个小球放到18个盒子里，每个里面最多放6个．所有盒子里都有小球，问最少几个盒子里的小球数目相同?（）
    A.2
    B.3
    C.4
    D.5


    答案：C
    解析：
    利用抽屉原理，按题干要求每个盒子里都有小球。最多放6个。可以从1到6构造6个抽屉，则问题转化为至少有几个含小球数目相同的盒子在同一个抽屉里。因为共有18个盒子．18+6：3。故假设每个抽屉里有3个盒子的小球数目是相同的，故18个盒子里放的小球最多有3×(1+2+3+4+5+6)＝63

相关内容