itgle.com

1、已知 f=lambda x:x*2, 则表达式 f（3) 的结果为____________.

题目

1、已知 f=lambda x:x*2, 则表达式 f（3) 的结果为____________.

相似考题

1.已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)

2.已知f(x)=x2+ax+3，若f(2+x)=f(2-x)，则f(2)=（）。A.0B.-1C.-2D.-3

3.已知函数f(x)={(1-tan2x)/(1+tan2x)}2 ,则f(x)的最小正周期是( ).(A)2π.(B)3/2π.(C)π.(D)π/2 .

4.已知f=lambdax:x+5，那么表达式f(3)的值为________。

参考答案和解析
∵函数f（x-1）=x 2 ∴f（x）=f[（x+1）-1]=（x+1） 2 =x 2 +2x+1 故选A．
更多“1、已知 f=lambda x:x*2, 则表达式 f（3) 的结果为____________.”相关问题

  • 第1题：

    已知函数f(x)=a2+k的图象经过点(1，7)，且其反函数f-1(x)的图像经过点(4，0)，则函数f(x)的表达式是 （ ）

    A．f(x)=4x+3

    B．f(x)=2x+5

    C．f(x)=5x+2

    D．f(x)=3x+5


    正确答案：A

  • 第2题：

    设f(x)是以2π为周期的周期函数，在[-π，π]上的表达式为f(x)=cos(x/2)，则f(x)的傅里叶级数为( ).

    A.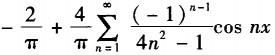
    B.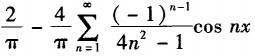
    C.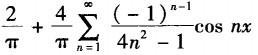
    D.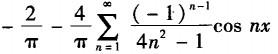

    答案：C
    解析：

  • 第3题：

    非负连续函数f(x)满足f(0)=0,f(1)=1.已知以曲线y=f(x)为曲边，以[0,x]为底的曲边梯形，其面积与f(x)的n+1次幂成正比，则f(x)的表达式为


    答案：
    解析：

  • 第4题：

    已知函数F（ ）、G（ ）的定义如下所示，执行表达式”x=F（3）”的运算时,若函数调用G（a）是引用调用方式,则执行”x=F（3）”后x的值为（ ）;若函数调用G（a）是值调用方式,则执行”x=F（3）”后x的值为（请作答此空）。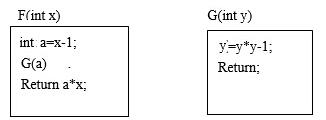

    A.6
    B.7
    C.8
    D.9

    答案：A
    解析：
    传值调用：形参取的是实参的值，形参的改变不会导致调用点所传的实参的值发生改变。引用（传址）调用：形参取的是实参的地址，即相当于实参存储单元的地址引用，因此其值的改变同时就改变了实参的值。本题的第一问:采用的是引用调用方式执行，x=3，a=2，G（a）中y=y*y-1=3，即a这时的值被修改为3，最后a*x=3*3=9 ;本题的第二问:采用的是传值调用方式执行，x=3，a=2；G（a）中y=y*y-1=3，即a这时的值仍然为2，最后a*x=2*3=6;

  • 第5题：

    已知g=lambda x，y=3，z=5：x+y+z，那么表达式g（2）的值为（）。


    正确答案:10

  • 第6题：

    已知f=lambda x：5，那么表达式f（3）的值为（）。


    正确答案:5

  • 第7题：

    已知f=lambda x：x+5，那么表达式f（3）的值为（）。


    正确答案:8

  • 第8题：

    已知f=lambda n：len（bin（n）[bin（n）.rfind（’1’）+1：]），那么表达式f（7）的值为（）。


    正确答案:0

  • 第9题：

    单选题
    已知函数x（t）的傅里叶变换为X（f），则函数y（t）=2x（3t）的傅里叶变换为（）
    A

    2X（f/3）

    B

    2/3X（f/3）

    C

    2/3X（f）

    D

    2X（f）


    正确答案： C
    解析： 暂无解析

  • 第10题：

    单选题
    已知f’（x）=tanx2，且f（0）=1，则f（x）等于（）．
    A

    tanx+x+1

    B

    tanx-x+1

    C

    -tanx-x+1

    D

    -tanx+x+1


    正确答案： B
    解析： 暂无解析

  • 第11题：

    填空题
    已知f=lambda x：5，那么表达式f（3）的值为（）。

    正确答案： 5
    解析： 暂无解析

  • 第12题：

    填空题
    已知f=lambda x：x+5，那么表达式f（3）的值为（）。

    正确答案： 8
    解析： 暂无解析

  • 第13题：

    数学运算

    已知f(x)＝x2+ax+3，若f(2+x)＝f(2-x)，则f(2)＝( )。

    A．0

    B．-1

    C．-2

    D．3


    正确答案：B
    [解析]本题答案为B。本题属于函数问题。由f(2+x)＝f(2-x)知道函数f(x)的对称轴为x＝ 2，因此-(a/2)＝2，a＝-4。所以f(2)＝22-2×4+3＝-1。

  • 第14题：

    已知f（x+1）=-1/f（x),若f(2)=2007,则f(2007)=( )


    A. 2
    B. -1/2007
    C. 1/2007
    D. 2008

    答案：B
    解析：
    解题指导： 由题意可得：X为奇数时f（x)=-1/2007，，X为偶数时f（x)=2007，故答案为B。

  • 第15题：

    已知f(x)，g(x)分别是定义在R上的偶函数和奇函数，且f(x)一g(x)=X3+x2+1，则f(1)+g(1)=( )。

    A.-3
    B.-1
    C.1
    D.3

    答案：C
    解析：
    令X＝﹣1，可得f(一1)-g(一1)=1，又由于f(x)，g(x)分别是定义在R上的偶函数和奇函数，即f(一l) ＝f(1)，g(-1)=g(1)，则f(一1) －g(1) ＝f( 1) ＋g(1)=1，所以答案为C。

  • 第16题：

    设f(x)为定义在R上的奇函数，当x≥0时,f(x)=2x+2x+b(b为常数)，则f(-1)=( )。

    A.3
    B.1
    C.-1
    D.-3

    答案：D
    解析：
    因为设f(x)为定义在R上的奇函数，故f(0)=20+2xO+b=0，得6=-1，即当x≥0时f(x)=2x+2x-1，故，f(1)=21+2x1-1=3，故f(-1)=f(1)=-3。

  • 第17题：

    已知函数x（t）的傅里叶变换为X（f），则函数y（t）=2x（3t）的傅里叶变换为（）

    • A、2X（f/3）
    • B、2/3X（f/3）
    • C、2/3X（f）
    • D、2X（f）

    正确答案:B

  • 第18题：

    已知f（x）=2x3+5，则f[1，2，3，4]=（），f[1，2，3，4，5]=（）。


    正确答案:2；0

  • 第19题：

    已知f=lambdax：x**2，那么表达式f（3）的值为（）

    • A、3
    • B、6
    • C、9
    • D、12

    正确答案:C

  • 第20题：

    设单调可微函数f(x)的反函数为g(x),f(1)=3,f′(1)=2,f″(3)=6则g′(3)=（）


    正确答案:1/2

  • 第21题：

    填空题
    已知f=lambda n：len（bin（n）[bin（n）.rfind（’1’）+1：]），那么表达式f（6）的值为（）。

    正确答案： 1
    解析： 暂无解析

  • 第22题：

    单选题
    已知f=lambdax：x**2，那么表达式f（3）的值为（）
    A

    3

    B

    6

    C

    9

    D

    12


    正确答案： C
    解析： 暂无解析

  • 第23题：

    填空题
    已知g=lambda x，y=3，z=5：x+y+z，那么表达式g（2）的值为（）。

    正确答案： 10
    解析： 暂无解析

  • 第24题：

    填空题
    已知f（x）=2x3+5，则f[1，2，3，4]=（），f[1，2，3，4，5]=（）。

    正确答案： 2,0
    解析： 暂无解析

相关内容