itgle.com

在所有的两位数10到99中任取一个数，这个数能被2或3整除的概率是1/3.

题目

在所有的两位数10到99中任取一个数，这个数能被2或3整除的概率是1/3.

相似考题

1.在所有的一位数中任取一个数，该数能被2整除的概率为（ ）。A．0.1B．0.3C．0.5D．0.7

2.有这样的两位数，它的两个数字之和能被4整除，而且比这个两位数大l的数。它的两个数字之和也能被4整除。所有这样的两位数的和是多少?A．102B．146C．118D．94

3.从1、2、3、4、5、6、7、8、9、10这10个数字中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?（ ）A．13B．14C． 18D． 20

4.从1，2，3，……，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于( )。A．0.3024B．0.0302C．0.2561D．0.0285

更多“在所有的两位数10到99中任取一个数，这个数能被2或3整除的概率是1/3.”相关问题

  • 第1题：

    从1,2,…,10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120。()


    正确答案:对

  • 第2题：

    请教:2011年宁夏公务员考试《行测》冲刺预测题(1)第2大题第14小题如何解答?

    【题目描述】

    第 44 题有这样的两位数，它的两个数字之和能被4整除，而且比这个两位数大1的数，它的两个数字之和也能被4整除。所有这样的两位数的和是多少（ ）

     


    正确答案：C
    答案分析：

    符合条件的两位数的两个数字之和能被4整除，而且比这个两位数大1的数.若十位 数不变，则个位增加1，其和便不能整除4，因此个位数一定是9，这种两位数有39、79。所以所求的和是39+ 79=118。

  • 第3题：

    现有以下程序： Private Sub Command1 Click（ ） c1=0 c2=0 For i=1 To 100 If i Mod 3=0 Then c1=c1+1 Else If i Mod 7=0 Then c2=c2+1 End If Next i Print c1+c2 End Sub 此程序运行后输出的是在1～100范围内（ ）。

    A.同时能被3和7整除的整数个数

    B.能被3或7整除的整数个数(同时被3和7整除的数只记一次)

    C.能被3整除，而不能被7整除的整数个数

    D.能被7整除，而不能被3整除的整数个数


    正确答案：B
    B。【解析】i是1到100的循环，在程序中，对3和7取模，显然就是3和7的倍数关系。需要注意的是If和else语句分别判断3和7的倍数而同时是21倍数的时候会不计，这有别于传统的计数方法。

  • 第4题：

    从1、2、3、4、5、6、7、8、9、10这10个数中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不l司的乘积？（ ）

    A．13

    B．14

    C．18

    D．20


    正确答案：A
    从整体考虑分两组，和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55，最接近的两组为27+28，所以共有27-15+1=13个不同的积。

  • 第5题：

    1、2、3、4、5、6、7、8、9这九个数字各用一次，组成三个能被9整除的三位数，这三个数的和最大是：

    A.2007
    B.2394
    C.2448
    D.2556

    答案：C
    解析：
    第一步，本题考查多位数问题。
    第二步，1—9这九个数字各用一次，先将1—9加和为45，组成三个能被9整除的三位数，可知每个三位数各位数字加和均为9的倍数，则三个三位数各位数字加和分别为9、18、18。
    第三步，要使这三个数的和最大，则每个三位数百位上的数字应尽量大，先考虑和为9的三位数，百位最大为6，这个三位数是621，剩余两个三位数最大分别为954和873，则954＋873＋621＝2448（可用尾数法，尾数为8）。

  • 第6题：

    从1，2，3，……，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于()。

    A:0.3024
    B:0.0302
    C:0.2561
    D:0.0285

    答案：A
    解析：
    该事件的概率=10*9*8*7*6/105=0.3024。

  • 第7题：

    从1到100的整数中任取一个数，则该数能被5或7整除的概率为（ ）

    A.0.02
    B.0.14
    C.0.2
    D.0.32
    E.0.34

    答案：D
    解析：

  • 第8题：

    从1到10这10个整数中任取3个数，恰有1个质数的概率是（ ）.


    答案：B
    解析：

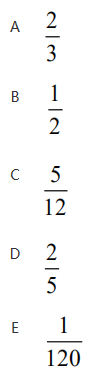
  • 第9题：

    从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于（）


    正确答案:0.3024

  • 第10题：

    一个两位数同时被2，3，5整除，这个数最大是多少？结果正确的是（）

    • A、30
    • B、90
    • C、95

    正确答案:B

  • 第11题：

    问答题
    35.从1，2．3，4，5中任取3个数字，则这3个数字中不含1的概率为

    正确答案：
    解析：

  • 第12题：

    问答题
    从0，1，2------9这十个数中不放回随机取4个数能排成4位偶数的概率P1与从中不放回随机取5个数能排成一个5位偶数的概率P2哪个大？

    正确答案： P1=P2
    解析： 暂无解析

  • 第13题：

    1到1000的整数(包含1和1000)中，至少能被2、3、5任意一个数整除的数共有(63)个。

    A．668

    B．701

    C．734

    D．767


    正确答案：C
    解析：这是一个典型的容斥原理的应用题。具体的解答思路如下。设A表示1到1000的整数(包含1和1000)中能够被2整除的数的集合；B表示1到1000的整数(包含1和1000)中能够被3整除的数的集合：C表示1到1000的整数(包含1和1000)中能够被5整除数的集合。则其中，符号表示对计算结果向下取整数。至少能被2、3、5任意一个数整除的数的个数为|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|=500+333+200-166-100-66+33=734

  • 第14题：

    从l、2、3、4、5、6、7、8、9、10这l0个数字中， 任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?( )

    A 1 3

    B．1 4

    C．18

    D．20


    正确答案：A
    15．A【解析】从整体考虑， 分两组和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55， 最接近的两组为27+28，所以共有27—15+1=13个不同的积。

  • 第15题：

    从2，3，4，5，6这五个数字中挑选两个，组成一个两位数，使其不能被3整除，则有多少种取法?


    正确答案：14

  • 第16题：

    在所有的1位数中任取一个数,这个数能被2或3整除的概率为________。

    A．1/2

    B．3/4

    C．7/10

    D．4/5


    正确答案：C
    解析：设A={取出的数能被2整除}={0,2,4,6,8},B={取出的数能被3整除}={0,3,6,9},则有A+B={取出的数能被2或3整除}={0,2,3,4,6,8,9},所以P(A+B)=7/10。

  • 第17题：

    从0到9这10个数中任取一个数并且记下它的值，放回，再取一个数也记下它的值。当 两个值的和为8时，出现5的概率是多少？


    答案：C
    解析：
    两个数值的和为8,则可能的情况有0+8、1+7、2+6、3+5、4+4、5+3、6+2、7+1、8+0这9种 情况，其中出现5的有2种情况。因此所求概率为2/9

  • 第18题：

    从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？

    A. 10%
    B. 30%
    C. 60%
    D. 90%

    答案：D
    解析：
    三个数中只要含有1就能满足，共C4,2=6种，三个数中含有2的话，三个数的和必须是偶数，共C3,2-1=2种，不含1和2只有3、4、5能被3整除，因此共有9种满足的情况，总数为c5,3=10，概率为9/10=90%。

  • 第19题：

    从0,1,2,3,4,5中任取3个数字,组成能被3整除的无重复数字的3位数有（ ）个

    A.18
    B.24
    C.36
    D.40
    E.96

    答案：D
    解析：

  • 第20题：

    从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于。

    A.0.3024
    B.0.0302
    C.0.2561
    D.0.0285

    答案：A
    解析：

  • 第21题：

    如果从1，2，…，10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120


    正确答案:正确

  • 第22题：

    从1，2，3，…，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除，问最多可取几个数（）

    • A、14个
    • B、15个
    • C、16个
    • D、17个

    正确答案:C

  • 第23题：

    单选题
    一个两位数同时被2，3，5整除，这个数最大是多少？结果正确的是()
    A

    30

    B

    90

    C

    95


    正确答案： A
    解析： 暂无解析

  • 第24题：

    单选题
    在1，2，3，…，40中，至少要取出几个数，才能保证取出的数中一定有一个数能被4整除？（）
    A

    3

    B

    4

    C

    21

    D

    31


    正确答案： D
    解析： 1，2，3，…，40中，能被4整除的有10个，因此最少要取出40-10+1=31个才能满足题干要求，选D。

相关内容