如图.已知圆⊙O是△ABC的外接圆,AD是圆⊙0的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB。 (1)求证:BE是⊙0的切线; (2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。
题目
如图.已知圆⊙O是△ABC的外接圆,AD是圆⊙0的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB。

(1)求证:BE是⊙0的切线;
(2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。

(1)求证:BE是⊙0的切线;
(2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。
相似考题
参考答案和解析
答案:
解析:
(1)连接OB,∵AD是圆⊙O的直径'∴∠OBD+∠EBD=90°, ∵BD=BC,∴其劣弧所对的圆周角相等,即∠CAB=∠BAD,
∵AO=BO,∴∠BAD=∠ABO,
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°,
∵B0是圆的半径,∴BE是⊙O的切线。
(2)设圆的半径为r,连接CD交OB于F,
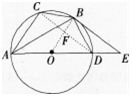
设圆的半径为R,连接CD,.

∵AO=BO,∴∠BAD=∠ABO,
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°,
∵B0是圆的半径,∴BE是⊙O的切线。
(2)设圆的半径为r,连接CD交OB于F,

设圆的半径为R,连接CD,.

更多“如图.已知圆⊙O是△ABC的外接圆,AD是圆⊙0的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB。 ”相关问题
-
第1题:
如图,在铅直面内有一圆板刻有三道光滑细槽AD、BD、CD,AD槽沿铅直方向,长为圆板直径,现有三个质量相等的小球在重力作用下自静止开始同时自A、B、C三点沿槽运动,下列四种情形中正确的是( )。 A.A球先到达D点
A.A球先到达D点
B.B球先到达D点
C.C球先到达D点
D.三球同时到达D点答案:D解析:
-
第2题:
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。答案:解析:(1)证明:∵PG=PD,∴∠PGD=∠PDG,又∵∠AGF=∠PGD,∠PDG=∠ABD,∴∠AGF=∠ABD,∴∠ADB=∠AFP=90°,∴AB为圆的直径。
-
第3题:
如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。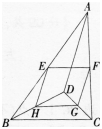 A.12
A.12
B.14
C.15
D.16答案:D解析:因为BD⊥CD,BD=8,CD=6,由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=
-
第4题:
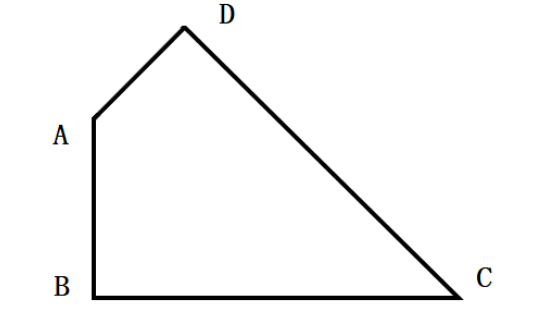
如图,已知一个四边形中边AD长为3cm,边BC长7cm;∠DAB=135°,∠ABC=∠ADC=90°那么这个四边形的面积是( )cm2。
 答案:D解析:第一步,本题考查几何问题,用割补平移法解题。
答案:D解析:第一步,本题考查几何问题,用割补平移法解题。
第二步,作BA和CD的延长线交于E,如图所示,得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB=135°,∠ABC=∠ADC=90°,可以求得∠DCB=360°-135°-90°×2=45°,且∠BEC=∠EAD=45°,所以△EBC和△ADE都是等腰直角三角形。
第三步,因为AD长3cm,BC长7cm,则BE=BC=7cm,DE=AD=3cm,所以
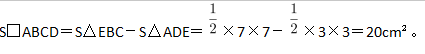
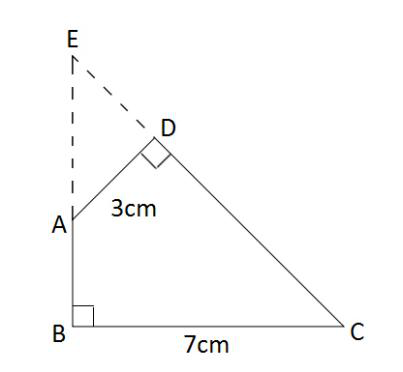
-
第5题:
如图所示,梯形ABCD的两条对角线AD、BC相交于O,EF平行于两条边且过O点。现已知AB=6,CD=18。问EF的长度为多少?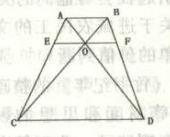 A. 8.5
A. 8.5
B. 9
C. 9.5
D. 10答案:B解析:解题指导: 18*BF/BD=6*DF/BD, BF/DF=1:3, OF/CD=1:4, OE/CD=1:4, EF=CD/2=9,故答案为B。 -
第6题:
如图6-6所示,D,E是△.ABC中BC边的三等分点,F是AC的中点,AD与EF交于O,则OF:OE=( ) A.1/2
A.1/2
B.1/3
C.3/4
D.9/10
E.2/3答案:A解析:接AE,由于F是AC的中点,D是CE的中点,因此O是△CAE的重心,所以,OF:OE=1:2 -
第7题:
圆截面杆ABC轴向受力如图。已知BC杆的直径d = 100mm,AB杆的直径为2d,杆的最大的拉应力是:A. 40MPa
B. 30MPa
C. 80MPa
D. 120MPa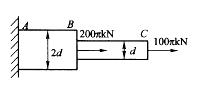 答案:A解析:
答案:A解析: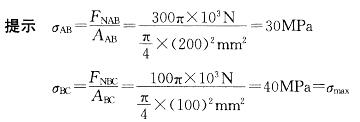
-
第8题:
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8, AB∥DE,求△DEC的周长。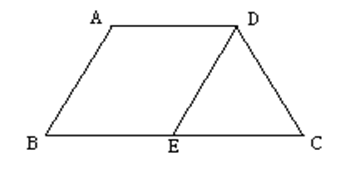 答案:解析:15
答案:解析:15 -
第9题:
如图在ΔABC中,DE∥BC,若AD:DB=1:3,DE=2,则BC等于( )。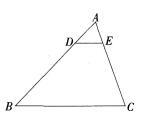 A.8
A.8
B.6
C.4
D.2答案:A解析:由于DE∥BC,所以DE:BC=AD:AB,又由AD:DB=1:3,所以AD:AB=1:4,由DE=2得BC=8。 -
第10题:
钢绞线的公称直径是钢绞线外接圆直径的准确尺寸
正确答案:错误 -
第11题:
舌位后、半高、唇圆的元音是()
- A、u
- B、<
- C、a
- D、o
正确答案:D -
第12题:
单选题车削外圆面时,待加工面直径为D,已加工面直径为D,则切削深度Ap()AD-D;
BD-D;
C(D-D./2;
正确答案: B解析: 暂无解析 -
第13题:
如图,四边形ABCD中,AB=10,AD=m,∠D=60o,以AB为直径作⊙O。
(1)求圆心0到CD的距离(用含m的代数式表示);
(2)当m取何值时,CD与⊙0相切?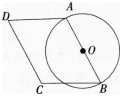 答案:解析:
答案:解析:
-
第14题:
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.答案:解析:
-
第15题:
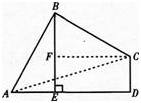
如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.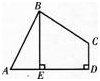
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.答案:解析: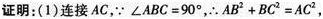
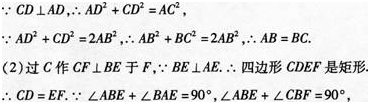

-
第16题:
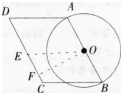
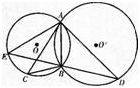
如图⊙O和⊙O’相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E.证明: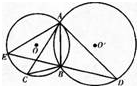
(1)AC?BD=AD?AB;
(2)AC=AE.答案:解析: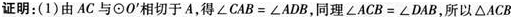

-
第17题:
已知△ABC的三边长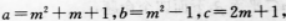 求△ABC的最大角的大小和外接圆半径R.答案:解析:由题意知
求△ABC的最大角的大小和外接圆半径R.答案:解析:由题意知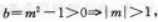


-
第18题:
如图6-9所示,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为( )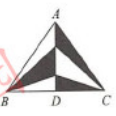 A.3
A.3
B.7.5
C.15
D.30
E.5.5答案:B解析:
-
第19题:
在△ABC中,∠C=90o,AC=8,BC=6,则△ABC的外接圆直径的长为__________ 。答案:解析:10 -
第20题:
圆截面杆ABC轴向受力如图5-5所示。已知杆BC的直径d=100mm,AB杆的直径为2d。杆的最大拉应力是()。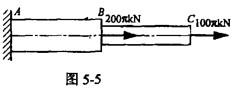
A. 40MPa B. 30MPa
C. 80MPa D. 120MPa答案:A解析:提示:求出最大轴力,按正应力公式计算。 -
第21题:
已知Rt△ABC中,斜边BC上的高AD=4,cosB=4/5,则AC=5。
正确答案:正确 -
第22题:
钢丝绳的直径是指其断面的外接圆直径。
正确答案:正确 -
第23题:
单选题钢绞线的公称直径是()的名义尺寸。A外接圆直径
B内接圆直径
C钢丝直径的和
D横截面投影当量圆直径
正确答案: A解析: 暂无解析
